3) zależność miedzy quasigeoidąa telluroidąw teorii Mołodenskiego

telluroida - obraz fizycznej powierzchni ziemi, nie jest powierzchniąekwipotencjalna, powierzchnia będącaaproksymacjąpowierzchni Ziemi w systemie geometrycznych

wysokości normalnych Molodenskiego, utworzonąprzez punkty, w których normalny

potencjał siły ciężkości jest równy potencjałowi rzeczywistemu punktów na powierzchni

Ziemi, leżących na tych samych normalnych liniach pionu, co punkty telluroidy, przy czym

odstępytelluroidy od powierzchni Ziemi sąpraktycznie równe wysokościom quasigeoidy nad

elipsoidąodniesienia.

Quasigeoida - teoretyczna powierzchnia aproksymująca swobodny poziom mórz i oceanów

do systemu wysokości normalnych, powierzchnia powstająca przez odłożeniewysokości

normalnych od punktów powierzchni Ziemi w kierunku ku elipsoidzie odniesienia, wzdłuż

normalnych linii pionu, przebieg zależy od rzeźby terenu.

2) Podaj różnicepomiędzyodstępem geoidy, a anomaliąwysokości.

Anomalia wysokości - wzniesienie quasi-geoidy nad elipsoidą

N - odstęp geoidy od elipsoidy H_ort= H_geom− N

Sposoby wyznaczenia odstępów geoidy od elipsoidy:

• interpolacja w/w odstępów (obliczamy znane odstępy, rozwiązanie równań

interpolacyjnych metodąnajmniejszych kwadratów, obliczamy wysokości

ortometryczne przez interpolację),

• wykonywanie niwelacji astronomicznej i pomiarów GPS (redukcja na geoidę

współrzędnych astronomicznych przez uwzględnienie krzywizny linii pionu),

• wykonywanie niwelacji trygonometrycznej i pomiar GPS (pomiar synchroniczny

odległości zenitalnej i obliczenie ΔN)

3) Do czego w "grawimetrii" wykorzystywane sąfunkcje Vening- Meinesza a do czego

Hirvonena.

Wzór VenigMeineszastosuje siędo obliczania odchyleńpionu. Określajązależność

między składowymi odchylenia pionu i odstępstwem geoidy. Przyjmuje się że składowa psi

jest dodatnia, kiedy rzeczywisty kierunek pionu odchyla sięna północ od normalnej do

elipsoidy. Składowa ni jest dodatnia, gdy rzeczywisty kierunek pionu odchyla sięna wschód.

Algorytm Hirvonenasłuży do transformacji współrzędnychortokartezjańskich

(prostokątnych) x, y, z na współrzędne geodezyjne B, L, H. Jest to proces iteracyjny. Zaletą

metody Hirvonena jest jej niezależność od pola siły ciężkości, a poprzez to pełna

odwracalność procedury. Mając dane B, L, H można ponownie obliczy x, y, z.

Algorytm obliczeń:

• obliczenie długości geodezyjnej L,

• obliczenie szerokości geodezyjnej, B dla k = 0,

• Na podstawie tego B₀ liczymy N₀ i H₀. Następniemając dane N₀ i H₀ liczymy na ichpodstawie B₁. Na podstawie B₁ liczymy N₁ i H₁ itd. Zazwyczaj wystarcza 3 iteracje.Proces jest powtarzany do uzyskania zadowalającejdokładności.

3. Wzory na składowe odchyleńpionu w funkcji odstępu geoidy od elipsoidy.

Przekształcenie wzorów Vening-Meinasza.

ds=Rd

ds=Rcos
dλ

→
,

3. Czym rożni siębezwzględne odchylenie pionu od względnego odchylenia pionu? Od czegogłownie zależy wartośćwzględnego odchylenia pionu.

Bezwzględne odchylenie pionu jest to kąt pomiędzy normalna do geoidy a odpowiednią normalną do elipsoidy ekwipotencjalnej (lub sferoidy normalnej). Elipsoida ma z założenia charakter globalny - obejmuję całą Ziemie - jej środek jest umieszczony w środku mas Ziemi zatem jej położenie względem geoidy jest stałe.

Względne odchylenie pionu jest kątem między normalną do geoidy a odpowiednią normalną

Do elipsoidy odniesienia.

Jego wartość uzależniona od współrzędnych B i L normalnej do elipsoidy odniesienia.

,
- składowe odchylenia pionu

PYTANIA SPISANE Z EGZAMINÓW I POPRAW Z SEMESTRU LETNIEGO 2007/2008

I zestaw

1. Związek spłaszczenia statycznego i spłaszczenia grawimetrycznego na powierzchni elipsoidy ziemskiej.

2. Interpolacja fizyczna redukcji Poincarego-Preya. Gdzie wykorzystuje się tą redukcję.

3. Pojęcie guasi-geoidy i telluroidy w systemie wysokości normalnej.

4. Co to jest dryft grawimetrii? Jak się go eliminuje?

5. Sposoby wyznaczania bezwzględnej wartości przyspieszenia ziemskiego.

II zestaw

1. Zależność spłaszczenia geometrycznego i grawimetrycznego Ziemi normalnej.

2. Interpolacja fizyczna redukcji Poincarego-Preya. Gdzie wykorzystuje się tą redukcję.

3. Rektyfikacja libeli poprzecznej grawimetru statycznego.

4. Pojęcie guasi-geoidy i telluroidy w systemie wysokości normalnej.

5. Uzupełnić jakiś taki wzór:

III zestaw

Potencjał normalny

Model potencjału siły ciężkości w postaci wyrażenia opisującego potencjał elipsoidy obrotowej przy zachowaniu warunków:

1. rozmiar i kształt elipsoidy są tak dobrane żeby powierzchnia elipsoidy była jak najlepszą aproksymacją geoidy

2. masa elipsoidy była równa masie Ziemi

3. prędkość kątowa wirowania elips wokół małej osi = prędkość kątowa wirow. Ziemi

4. pow. przyjętej elipsoidy ma być z definicji powierzchnią ekwipotencjalną o potencjale u0= rzeczywistemu potencjałowi siły ciężkości geoidy u0=w0=const.

5. Potencjał zakłócający jest to różnica potencjału rzeczywistego siły ciężkości i potencjału normalnego siły ciężkości T(vp)= w(vp) - u(vp)

geoida (w0)- potencjał rzeczywisty , elipsoida (u0)- potencjał normalny

IV zestaw

1. Na jakiej wysokości nad Ziemią przyciąganie zmaleje do połowy wartości na jaj powierzchni?

Obliczenia wykonaj dla R (WGS'84)

2. Oblicz przyciąganie płyty Bouguera o promieniu podstawy A zmierzającym do nieskończoności i wysokości H=200m

oblicz wartość anomalii Bouguera w tym pkt. wyjaśnij symbole A we wzorze na anomalie

dane:

Fi =41stopni 30 minut

G pom= 987052 mGal

σ =2,5 g cm^-3

3. Omów zasadę wyznaczania odchyleń pionu. Jakie dane mogą być wykorzystywane do wyznaczania wartości odchyleń pionu. W jaki sposób oblicza się te wartości?

4. Omów system wartości ortometrycznych. Które z wartości występujących we wzorze wyrazającym wartość ortometryczną punktu świadczy o systemie wysokości i co ona reprezentuje ?

V zestaw

1. związek spłaszczenia grawimetrycznego i geometrycznego powierzchni ekwipotencjalnej

2. interpretacja redukcji terenowej do przyśpieszenia ziemskiego.

3. źródła poprawki pływowej do przyśpieszenia.

4. różnica symetrycznej i niesymetrycznej metody pomiarów balistycznych.

5. wzór na wysokość geopotencjalną i jakie właściwości mają te wysokości.

VI zestaw

1. Wyrazić zależność spłaszczenia statycznego J₂ od grawimetrycznego β.

2. Składowe podstawowej osnowy grawimetrycznej kraju.

3. Trzy rodzaje redukcji topograficznej ciężkości.

4. Zależność składowych odchyleń pionu od odstępu geoidy.

5. Podać sposób na wyznaczenie odstępów geoidy od quasi-geoidy.

VII zestaw

1. Na jakiej wysokości nad Ziemią przyciąganie osiąga wartość 0?

Obliczenia wykonaj dla R (WGS'84)

2. Omów teorię Izostazji i scharakteryzuj redukcję izostatyczną.

3. Omów rysunek ( zagadnienie odchylenia pionu), wyjaśnij jaka jest istota bezwzględnego odchylenia pionu i co możemy na jej podstawie określić.

4. Oblicz różnice wysokości punktów wyrażonych w systemie ortometrycznym i normalnym.

Dane:

Fi= 49,53667

Lambda= 20,28667

H=1265,32 m

G pom=982344,4 mGal

5. Omów zasady projektowania i wykonywania niwelacji precyzyjnej.

VIII zestaw

1. Oblicz przyciąganie płyty Bouguera o promieniu podstawy a , zmierzającym do nieskończoności i wysokości H= 3000 m

Oblicz wartość anomalii Bouguera w tym punkcie. Wyjaśnij symbole we wzorze na anomalię.

Fi= 39 stopni i 30 minut

G pom= 978052 mGal

Sigma= 2,5 g cm^-3

Omów istotę tej anomalii i jej wykorzystanie praktyczne.

2. W jaki sposób można wyznaczyć wartość kąta odchylenia pionu w punkcie mając mapy anomalii Faye'a?

3. Oblicz wysokość punktu wyrażoną w systemie wysokości dynamicznych mając dane:

Fi= 39,53667

Lambda= 20,28667

Hⁿ=1285,32 m

G pom= 962344,4 mGal

Sigma= 2.5 g cm ^-3

4. Omów warunki w jakich powinno się wykonywać pomiar ( pogoda, wykonywanie pomiarów)

GEODEZJA FIZYCZNA - EGZAMIN 2004

Termin I

1. Przedstaw na rys. relacje parametrów, u, v, Ω elipsoid równowagi ciała wirującego. Podaj objaśnienia dotyczące figur granicznych oraz punktu b_i-furkacyjnego.

2. Różnice w redukcjach i anomaliach przyspieszenia ziemskiego ziemskiego teorii Stoeksa i Mołdienskiego badania figury Ziemi.

3. Wyjaśnić, jakie trzy macierze należy zestawić przy predykcji anomalii z minimalną dyspersją. Podać znaczenie symboli tam zawartych.

4. Podać zasadę astatyzacji grawimetrów statycznych.

5. Wpływy istnienia atmosfery na wskazania grawimetru ( i statycznego i dynamicznego ).

6. Pojęcie topograficznego odchylenia pionu.

Termin II

1. Co to jest rząd sferoidy? Dla sferoidy Brunsa podać zależność spłaszczenia geometrycznego i statycznego.

2. Sformułować problem Bjerhammara. Objaśnić rozwiązanie gradientowe tego zadania.

3. Zasada działania grawimetru nadprzewodnikowego.

4. Wjaśnić, dlaczego ruch bieguna przejawia się we wskazaniach grawimetru.

5. Dlaczego topograficzne odchylenia pionu nie są równe określonym przy użyciu wzorów Vening-Mainesza?

6. Korzystając z rysunku podać i objaśnić zasadnicze parametry funkcji kowariancji anomalii grawimetrycznych.

Termin IV

1. Jaką figurę Ziemi Normalnej nazywa się sferoidą jednoparametrową? Co jest tym parametrem?

2. Sformułowanie tzw. problemu Bjerhammara. Cztery sposoby rozwiązania.

3. Przedstaw sposób predykcji z minimalną dyspersją anomalii grawimetrycznej do punktu P na podstawie anomalii w punktach K₁, K₂, ..., K_n.

4. Omówić proces przejścia od grawimetrycznych odchyleń pionu (całkowanie do 1000km) do względnych odchyleń pionu (np. układ WGS'84).

5. Jaką zasadę wykorzystano przy konstrukcji grawimetru nadprzewodnikowego?

6. Omówić pomocnicze prace pomiarowe, niezbędne do właściwego opracowania wyznaczeń grawimetrem absolutnym.

Pytania na egzamin:

1. Wyjaśnić pojęcia: sferoida normalna, elipsoida poziomowa, geoida, telluroida, figura równowagi, quasi-geoida. Która z nich jest powierzchnią ekwipotencjalną?

2. Wychodząc z warunku równowagi Maclaurina i wzoru na spłaszczenie statyczne sferoidy wyprowadzić wzór na J₂ elipsoidy poziomowej.

3. Udowodnić, że dla modelu Roche'a α_max=½.

4. Rozwiązanie problemu Mołdienskiego opiera się na równaniu
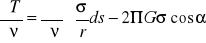
   . Podać objaśnienia symboli. Rysunek niezbędny.

5. Sposoby rozwiązania redukcji anomalii w problemie Bjerhammara.

6. Objaśnić, na czym polega nowe rozwiązanie w konstrukcji aparatu wahadłowego zbudowanego w PW.

7. Wyjaśnić, dlaczego aparat balistyczny z podrzutem jest dokładniejszy od swobodnego spadku.

8. Przedstaw na rysunku i podać równanie wagi astatyzowanej.

9. Idea budowy grawimetru Worden; idea budowy grawimetru LaCoste-Romberg.

10. Wymień i omów parametry empirycznej funkcji kowariancji. Naszkicuj jej przebieg i funkcji struktury.

11. Co to jest i do czego się wykorzystuje prawo propagacji kowariancji elementów pola siły ciężkości?

12. Dane wyjściowe i sposób uzyskania empirycznej funkcji kowariancji Cov_s (ξ^ag ; ξ^gr ).

13. Różnice predykcji z minimalną dyspersją i kolokacji metodą najmniejszych kwadratów.

14. Dwa efekty ruchu bieguna w ciężkości ziemskiej.

15. Omówić wpływ ciśnienia powietrza (trojaki) na wskazania grawimetru.

16. Wymień czynniki wpływające na luno-solarną poprawkę do przyspieszenia. Jak na tym tle kształtuje się poprawka Honkasalo?

17. Podać objaśnienia odnośnie do topograficznego odchylenia pionu.

18. Jakie dane wyjściowe niezbędna SA do wykonania niwelacji astronomiczno-grawimetrycznej między punktami, na których nie wykonano pomiarów astronomicznych φ i λ.

19. Zasadnicze elementy krajowej sieci grawimetrycznej.

20. Wyjaśnić, przy użyciu rysunków, wpływ pola siły ciężkości przy przenoszeniu współrzędnych punktu z wysokiego komina na płaszczyznę odniesienia.

21. Ogólne zasady planowania zdjęcia grawimetrycznego w celu wyznaczenia odchyleń pionu z wysoką dokładnością.

22. Dlaczego tylko niektóre z elipsoid jednorodnych mogą być sferoidami? Podaj warunki tożsamości.

23. Omówić trzy graniczne zagadnienia teorii potencjału grawitacyjnego.

24. Wyprowadzić wzór na deformację geoidy redukcją Faye'a (Bougera, izostatyczną).

25. Krótko objaśnić na czym polega sposób interpolacji anomalii Bougera, polegający na wykorzystaniu współczynnika korelacji tych anomalii z wysokością przez kowariancję składników.

26. Przeprowadzić dyskusję równania
    

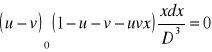
27. Dlaczego dla modelu Roche'a J₂=J₄=...=0?

28. Sposób rektyfikacji libeli czułości w grawimetrze astatyzowanym.

29. Objaśnić w jakim przypadku stosuje się uogólnioną funkcję Stoeksa S(r,ψ). Niezbędny rysunek.

30. Proces przejścia od grawimetrycznych do względnych odchyleń pionu.

31. Procedura określania przyspieszenia siły ciężkości na zmiany współrzędnych φ i λ na drodze od f.p.Z. do geoidy.

32. Przedstaw sytuację dla której anomalia Faye'a i Bougera będą jednakowe.

33. Które ze znanych Ci przyrządów grawimetrycznych (nie tylko grawimetrów astatyzowanych) nie wymagają kalibracji i dlaczego?

34. Wpływ ciężkości na drgania struny w grawimetrze dynamicznym.

35. W rozwiązaniu równania Greena, przy wartości Poissona 4πG ∫∫∫ σVdτ występują całki, noszące nazwę stałych Stoeksa. Do czego służy zatem J₀, J₁¹, J₁², J₁³ ?

36. Co oznacza rząd sferoidy? Co to jest sferoida Brunsa, a co sferoida Helmerta?

37. Przedstawić koncepcję określenia spłaszczenia geometrycznego normalnej Ziemi na podstawie informacji geometrycznych

38. Objaśnić pojęcie normalnej atmosfery ziemskiej.

39. Jaką zasadę wykorzystano przy konstrukcji grawimetru nadprzewodzącego.

40. W jaki sposób określić odstęp geoidy od quasigeoidy Mołdienskiego? Czy potrafisz ustalić funkcję ustalającą zależność J-N od anomalii grawimetrycznych (jakich)?

41. Podaj sposób oceny dokładności powierzchniowego zdjęcia grawimetrach=znego i mapy grawimetrycznej.

42. Wymienić dane niezbędne do przejścia od różnic wysokości w systemie normalnym (obowiązującym w Polsce) do przewyższeń ortometrycznych, obowiązujących w państwach Unii Europejskiej.

1. redukcja anomalii w podejściu Bjerhammara
   2. czy funkcja siły odśrodkowej jest harmoniczna
   3. Wzór Stokesa i wskazać w nim anomalie

1. Podać definicję spłaszczenia grawimetrycznego. Wymienić inne stałe grawimetryczne rzędu spłaszczenia.
   2. Napisać laplasjan z potencjału odśrodkowego (wzór na potencjał był dany).
   3. Problem Bjerhammara. Podać i krótko scharakteryzować podejścia do rozwiązania.

1. Napisac wzór na Laplasjan potencjału odśrodkowego wyrażonego wzorem V=2omega^2(x^2+y^2).(albo jakiś podobny wzór)
   2. Czym różni się anomalia właściwa w teorii Stokesa od anomalii mieszanej w teorii Mołodeńskiego wyznaczania figury (kształtu) Ziemi?
   3. Wzory na składowe odchyleń pionu w funkcji odstępu geoidy od elipsoidy.

1. Podać podstawowe równanie geodezji fizycznej w teorii Stokesa i opisać składniki.
   2. Podaj różnice pomiędzy odstępem geoidy, a anomalią wysokości.
   3. Do czego w "grawimetrii" wykorzystywane są funkcje Vening- Meinesza a do czego Hirvonena.

1. Definicja spłaszczenia statycznego sferoidy, kiedy jest równe 0?
   2. wyraz Brunsa we podstawowym równaniu geodezji fizycznej
   3. zależnosc miedzy quasigeoidą a telluroidą w teorii Mołodenskiego

1. gdzie zdefiniowany jest warunek graniczny w teorii Mołodeńskiego
   2. dlaczego potencjał Newtona jest funkcją harmoniczną a potencjał odśrodkowy nie jest funkcją harmoniczną
   3. na czym polega rozwiązanie gradientów coś tam z Bjerhammerem...

1. Wyjaśnić pojęcie spłaszczenia grawimetrycznego
   2. Obliczyć laplasjan funkcji potencjału siły odśrodkowej, danego wzorem:
   
   u=omega^2/2*(x^2+y^2) (chyba tak to leci)
   
   3. Wyjaśnić w kilku zdaniach problem Bjerhammara i omówić 4 podejścia jego

rozwiązania.

GRUPA A

1) Definicja spłaszczenia statycznego. Kiedy jest równe 0?

J₂ =
, gdzie C, A - główne momenty bezwładności

lub w przybliżeniu J₂ =

J₂ = 0 jeżeli sferoida ma spłaszczenie geometryczne α = 0, tzn. w przypadku kuli

J₂ = 0 jeżeli przyspieszenie siły ciężkości na równiku sferoidy γ_e = 0

2) Wyraz Brunsa w podstawowym równaniu geodezji fizycznej

podstawowe równanie geodezji fizycznej, które definiuje związek między anomalią grawimetryczną i potencjałem zakłócającym. Pierwszy wyraz to anomalia właściwa (pochodna potencjału zakłócającego), drugi składnik to wyraz Brunsa (określa wpływ odstępu powierzchni ekwipotencjalnych w polu rzeczywistym i normalnym). Wzór Brunsa: N=T/γ

T=W-U (W-potencjał rzeczywisty, U-normalny); γ - przyspieszenie normalne.

3) zależnosc miedzy quasigeoidą a telluroidą w teorii Mołodenskiego

telluroida - powierzchnia będąca aproksymacją powierzchni Ziemi w systemie geometrycznych wysokości normalnych Molodenskiego, utworzoną przez punkty, w których normalny potencjał siły ciężkości jest równy potencjałowi rzeczywistemu punktów na powierzchni Ziemi, leżących na tych samych normalnych liniach pionu, co punkty telluroidy, przy czym odstępy telluroidy od powierzchni Ziemi są praktycznie równe wysokościom quasigeoidy nad elipsoidą odniesienia.

Quasigeoida - powierzchnia powstająca przez odłożenie wysokości normalnych od punktów powierzchni Ziemi w kierunku ku elipsoidzie odniesienia, wzdłuż normalnych linii pionu.

GRUPA B

1) Podać podstawowe równanie geodezji fizycznej w teorii Stokesa i opisać składniki.

patrz -> gr A 2)

dodatkowo: n - normalna do geopa (powierzchni o równaniu W = const)

2) Podaj różnice pomiędzy odstępem geoidy, a anomalią wysokości.

Anomalia wysokości - wzniesienie quasi-geoidy nad elipsoidą

3) Do czego w "grawimetrii" wykorzystywane są funkcje Vening- Meinesza a do czego Hirvonena.

Wzór Venig Meinesza stosuje się do obliczania odchyleń pionu

E

1. redukcja anomalii w podejściu Bjerhammara

2. czy funkcja siły odśrodkowej jest harmoniczna

nie jest, natomiast można ją przybliżyć funkcją harmoniczną

str. 104 Czarnecki

str. 85 równanie Laplace'a

3. Wzór Stokesa i wskazać w nim anomalie

Ag - anomalia grawimetryczna

S(ψ) - funkcja Stokesa

ψ - odległość sferyczna między punktem, w którym wyznaczony jest odstęp, a bieżącym punktem, w którym określono anomalię

ds - element powierzchni

γ - średnie przyspieszenie normalne

R - średni promień Ziemi przyjętej za kulę

F

1. Czym różni się potencjał siły ciężkości od potencjału atrakcyjnego? Czy to są wektory, czy skalary?

Pole potencjału siły ciężkości jest sumą pola atrakcyjnego (siły przyciągania) i pola siły ciężkości

W(A) = V(A) + u(A)

Potencjał siły ciężkości i atrakcyjny to skalary.

2. Podać parametry Ziemi Normalnej posiadające wartości rzędu spłaszczenie Ziemi i objaśnienia symboli.

J₂ - spłaszczenie statyczne

a, e², e'² - długość dłuższej półosi, kwadrat mimośrodu

- spłaszczenie grawimetryczne, przyspieszenie graw. na biegunie (p) i równiku (e)

- parametr dynamiczny

3. Czym rożni się bezwzględne odchylenie pionu od względnego odchylenia pionu? Od czego głownie zależy wartość względnego odchylenia pionu.

Bezwzględne odchylenie pionu - kąt między kierunkiem linii pionu i kierunkiem normalnej do elipsoidy ziemskiej.

Względne odchylenie pionu - kąt między kierunkiem linii pionu i kierunkiem normalnej do elipsoidy odniesienia.

dN = - θ ds θ - odchylenie pionu, dN - przyrost odstępu , ds - przyrost odległości

G

1. Objaśnić gdzie zdefiniowany jest warunek graniczny w teorii Mołodeńskiego badania kształtu Ziemi.

2. Dlaczego potencjał Newtona jest funkcją harmoniczną, a potencjal siły odśrodkowej nie jest takaa funkcją?

3. na czym polega tzw. rozwiązanie gradientowe "problemu Bjerhammara"?

H

1. dlaczego potencjał odśrodkowy nie jest funkcją harmoniczną?

2. podać wzór na warunek graniczny geodezji fizycznej w myśl teorii Stokesa i wskazać w nim anomalię właściwą (zaburzenie grawitacyjne)

3. co to jest anomalia zredukowana w rozwiązaniu tzw. problemu Bjerhammara?

1. Dwie przyczyny rozbieżności siły ciężkości między biegunem a równikiem ziemskim. Spłaszczenie grawimetryczne sferoidy.

2. Pojęcie ziemi normalnej, jej stałe fundamentalne

3. Przyczyny zmiany ciężkości od równika do bieguna ziemskiego

4. Różnice koncepcji Stokesa i Mołodieńskiego badania kształtu Ziemi

5. Interpretacja fizyczna redukcji Bouguera i jej efekt pośredni, do czego się ją wykorzystuje

6. Parametry drugiego rzędu alfa^2 Ziemi Normalnej

7. Definicja spłaszczenia statycznego przez moment bezwładności ciała

8. Zasadnicze równanie grawimetrii: zalezność anomalii graw Ag od potencjału zakłócającego

9. Zalezność J2 od alfa, objaśnienia

10. Składowe redukcji PP, rysunek i etapy

11. Redukcja topograficzna

12. Spłaszczenie dynamiczne Ziemi

13. Interpretacja fizyczna (rysunki) redukcji terenowej, jako redukcji topograficznej przyspieszenia ziemskiego

14. Trzy rodzaje poprawek topograficznych do przyspieszenia ziemskiego

15. ? Podać dwa prawa Claurianta dla powierzchni ekwipotencjalnej i objaśnic symbole

16. Warunki jakie powinny spełniać redukcje grawimetryczne w teorii Stokatesa

17. ? Zinterpretować wzory Veniga-Mainesza przy użyciu rysunków ksi=dN/dx, ni-dN/dy

18. ? Wysokość w każdym systemie wyraza się wzorem H=-(wo-wa)/g. w jaki sposób wylicza się wartośc licznika ilorazu?

19. Związek spłaszczenia statycznego i spłaszczenia grawimetrycznego na powierzchni elipsoidy ziemskiej

20. Interpolacja fizyczna redukcji Poincarego-Preya. Gdzie wykorzystuje się tą redukcję.

21. Sposoby wyznaczania bezwzględnej wartości przyspieszenia ziemskiego.

22. Zależność spłaszczenia geometrycznego i grawimetrycznego Ziemi normalnej.

23. Uzupełnić jakiś taki wzór:
    

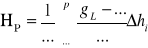
24. Jakie składowe zawiera redukcja Bouguera?

25. Objaśnij symbole na anomalię Fayea. Gdzie jest wykorzystywana?

26. ? Która z wielkości występujących we wzorze H=(w-wg)/g świadczy o wysokości i dlaczego?

27. Na jakiej wysokości nad Ziemią przyciąganie zmaleje do połowy wartości na jaj powierzchni?

Obliczenia wykonaj dla R (WGS'84)

(dane wzorki)

28. Oblicz przyciąganie płyty Bouguera o promieniu podstawy A zmierzającym do nieskończoności i wysokości H=200m. oblicz wartość anomalii Bouguera w tym pkt. wyjaśnij symbole A we wzorze na anomalie Fi =41stopni 30 min, G pom= 987052 mGal, σ =2,5 g cm^-3

(dane wzorki)

29. ? Omów zasadę wyznaczania odchyleń pionu. Jakie dane mogą być wykorzystywane do wyznaczania wartości odchyleń pionu. W jaki sposób oblicza się te wartości?

30. związek spłaszczenia grawimetrycznego i geometrycznego powierzchni ekwipotencjalnej

31. interpretacja redukcji terenowej do przyśpieszenia ziemskiego.

32. źródła poprawki pływowej do przyśpieszenia.

33. Wyrazić zależność spłaszczenia statycznego J₂ od grawimetrycznego β.

34. Trzy rodzaje redukcji topograficznej ciężkości.

35. Na jakiej wysokości nad Ziemią przyciąganie osiąga wartość 0?Obliczenia wykonaj dla R (WGS'84)

36. W jaki sposób można wyznaczyć wartość kąta odchylenia pionu w punkcie mając mapy anomalii Faye'a?

ds

dN

N

θ

.

.

geoida

elipsoida

poziomowa

---