Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się ze sposobem pomiaru amplitudy i fazy poszczególnych harmonicznych przebiegów niesinusoidalnych oraz praktyczna realizacja pomiaru współczynnika zawartości harmonicznych przebiegów niesinusoidalnych.

Metoda pomiaru.

Wszystkie pomiary przeprowadzane zostały w układzie pomiarowym przedstawionym na rysunku 1:

Rysunek 1

Wyłączniki W1 - W6 służą do uzyskiwania różnych konfiguracji układu, koniecznych do realizacji poszczególnych punktów pomiarowych. Filtr pasmowo-przepustowy jest układem o przestrajanej częstotliwości, zapewnia on wzmocnienie równe - 1 dla ustalonej częstotliwości.

Pomiar amplitudy i fazy poszczególnych harmonicznych przebiegów niesinusoidalnych.

Pomiary zostały przeprowadzone dla wyłączników w₁, w₂, w₃, w₅, w₆ zamkniętych.

Do układu podłączyliśmy oscyloskop w ten sposób, że kanał A oscyloskopu jest dołączony do wyjścia generatora, a kanał B do wyjścia układu. Następnie zaczynając pomiary od częstotliwości 100 Hz z ekranu oscyloskopu dla każdego przebiegu wyznaczaliśmy amplitudę i fazę. Potem zmienialiśmy częstotliwość rezonansową filtru za pomocą przełącznika zmiany zakresu i pokręteł regulacji częstotliwości tak, aby dostroić filtr do częstotliwości poszczególnych harmonicznych badanego przebiegu ( odpowiadało to maksymalnej amplitudzie przebiegu wyjściowego w układu ). Wyniki pomiaru przedstawione są w tabeli 1.

Taka metoda pomiarowa była możliwa dzięki wykorzystaniu właściwości filtru środkowo - przepustowego tzn. filtru który z całej szerokości pasma częstotliwościowego przepuszcza tylko wąskie pasmo częstotliwość znajdujących się wokół częstotliwości wybranej f₀, a tłumi częstotliwości poza tym pasmem. Przykładową charakterystykę takiego filtru przedstawia rysunek 2. Ponieważ poszczególne harmoniczne są wielokrotnością podstawowej harmonicznej, więc dzięki odpowiednio dużej selektywności filtru możemy przepuszczać przez filtr tylko wybrane częstotliwości regulując częstotliwością rezonansową. Regulację tę przeprowadzaliśmy za pomocą pokręteł umieszczonych na pulpicie filtru. Dzięki temu możliwe było przepuszczanie przez filtr wybranej częstotliwości charakterystycznej dla danej harmonicznej i tłumienie pozostałych. Przykładowym filtrem środkowo - przepustowym może być filtr RC typu 2T lub filtr LC.

Rysunek 2

Pomiar współczynnika zawartości harmonicznych przebiegów niesinusoidalnych.

W celu wykonania pomiarów wykorzystaliśmy miernik zniekształceń nieliniowych. Miernik ten podłączyliśmy do wyjścia generatora. Następnie dla kolejnych przebiegów wyjściowych generatora dokonywaliśmy pomiarów współczynnika zawartości harmonicznych. Wyniki pomiarów przedstawia tabela 2. Współczynnik zawartości harmonicznych k_h obliczaliśmy ze wzoru:

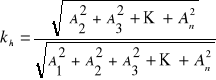
Tabele pomiarowe.

Przebiegi
Wartość maksymalna	[ V ]		7,5		6
Składowa stała	[ V ]		0		0
Wartość maksymalna	Numer harmonicznej		Wartość zmierzona	Wartość obliczona	Wartość zmierzona	Wartość obliczona
		1	[ V ]	5,5	6,09	7,5
		2	[ V ]	-	-	-	-
		3	[ V ]	0,34	0,68	1,6
		4	[ V ]	-	-	-	-
		5	[ V ]	0,03	0,24	0,7
		6	[ V ]	-	-	-	-
		7	[ V ]	0,016	0,12	0,4
		8	[ V ]	-	-	-	-
		9	[ V ]	0,005		0,075
	Faza początkowa harmonicznych	1	[ ° ]	0	0	0	0
		2	[ ° ]	-	-	-	-
		3	[ ° ]	180	180	0	0
		4	[ ° ]	-	-	-	-
		5	[ ° ]	0	0	0	0
		6	[ ° ]	-	-	-	-
		7	[ ° ]	180	180	0	0
		8	[ ° ]	-	-	-	-
		9	[ ° ]	0	0	0	0

Lp.	Przebieg	Wartość skuteczna	Składowa stała	Współczynnik kh
								Pomierzony	Obliczony
-	-	[ V ]	[ V ]	[ % ]	[ % ]
1.		4,34	0	11	12
2.		1,87	0	35	39,6

Obliczenia.

Wartości poszczególnych harmonicznych wynoszą:

1. przebiegu
   :

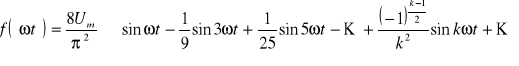
U_m1 = 6,09 V U_m3 = 0,68 V U_m5 = 0,24 V U_m7 = 0,12 V U_m9 = 0,08 V

2. przebieg
   :

U_m1 = 2,43V U_m3 = 0,81V U_m5 = 0,49V U_m7 = 0,35V U_m9 = 0,27V

Wartość skuteczna obliczona ze wzoru

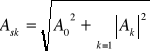
Dla przebiegu
wynosi ona:

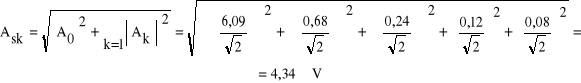
Dla przebiegu
wynosi ona:

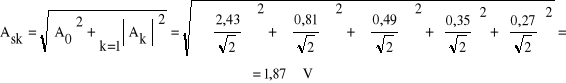
Dla przebiegu
kh wynosi:

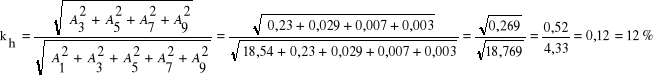
Dla przebiegu
k_h wynosi:

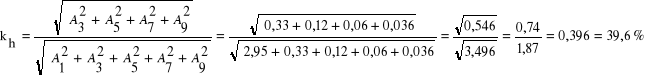
Wnioski.

W ćwiczeniu badaliśmy przebiegi: trójkątny i prostokątny. Ponieważ funkcje trójkątna i prostokątna są funkcjami nieparzystymi f(-t) = - f(t), dlatego w szeregu Fouriera współczynniki c_k się zerują. Dodatkowo funkcje te są antysymetryczne (f(t+T/2)= - f(t)), co powoduje, że wszystkie współczynniki o wyrazach parzystych również się zerują. Wartość składowej stałej tych przebiegów jest równa 0.

W ćwiczeniu dokonaliśmy pomiaru amplitud dla 1, 3, 5, 7 i 9 harmonicznej tych sygnałów. Tak mała liczba pomiarów ma na pewno wpływ na różnicę, jaka występuje pomiędzy obliczonym i zmierzonym współczynnikiem zawartości harmonicznych, a także na różnicę wartości skutecznej tego przebiegu obliczoną z wzoru Parsevala tj.
.

Dla obu przebiegów wartość obliczona współczynnika zawartości harmonicznych jest nieznacznie większa od wartości otrzymanych z pomiarów. Ta niewielka niezgodność, jaka występuje pomiędzy tymi wartościami może być spowodowana faktem, że w rzeczywiste przebiegi mogą nieco różnić się od teoretycznych. Powoduje to pojawienie się dodatkowych harmonicznych, co ma wpływ na wskazania miernika.

Należy zauważyć, że obliczone wartości maksymalne poszczególnych harmonicznych różnią się od wartości pomierzonych, ale nie miało to istotnego wpływu na wynik pomiaru współczynnika zawartości harmonicznych.

Największe znaczenie dla dokładności pomiarów ma:

• dokładność dostrajania filtru

• możliwości odczytu z ekranu oscyloskopu.

Reasumując uzyskane wyniki można stwierdzić, że:

• szereg Fouriera z zadawalającą dokładnością odwzorowuje okresowe przebiegi niesinusoidalne.

• współczynnik k_h zależy w dużym stopniu od liczby harmonicznych występujących w przebiegu, a więc zależy od rodzaju symetrii występującej w przebiegu i jest tym mniejszy im więcej tych symetrii występuje w danym przebiegu.

3

5

---