Rogoż Mateusz 2006-04-23

I ED L-6

Wyznaczanie ogniskowej soczewki metodą Bessela

Sprawozdanie z ćwiczenia nr 48

I. Zagadnienia teoretyczne.

Przechodzenie światła przez ośrodki przezroczyste

Światło w jednolitym ośrodku przezroczystym porusza się wzdłuż linii prostej, nie zmieniając kierunku. Światło w wyniku zmiany ośrodka, w jakim się rozchodzi, załamuje się - wraz ze zmianą ośrodka dochodzi najczęściej do zmiany kierunku rozchodzenia się światła.

Załamanie światła powoduje szereg ciekawych efektów - m.in. złudzenie "złamania" łyżeczki od herbaty umieszczonej w szklance, nieprawidłowej lokalizacji dna jeziora, gdy patrzymy na nie z brzegu. Załamanie światła jest wykorzystywane do budowy soczewek stosowanych w okularach, obiektywach aparatów, lunetach i innych przyrządach optycznych.

Załamanie występuje m.in., gdy światło przechodzi:

• z powietrza do wody,

• z wody do powietrza,

• ze szkła do powietrza,

• z powietrza do szkła,

• z warstwy powietrza gęstszego do rzadszego.

Ogólnie - światło będzie się załamywać prawie zawsze, gdy zmienia się ośrodek. Załamanie zawsze wiąże się ze zmianą ośrodka, bo istnieje podobne w nazwie zjawisko optyczne - ugięcie, które może się pomylić z załamaniem. Ugięcie ma inną naturę (zachodzi w jednym ośrodku) i inaczej przebiega, więc łatwo o pomyłkę. Załamanie światła jest podstawowym zjawiskiem, na którym opiera się funkcjonowanie soczewek i pryzmatów.

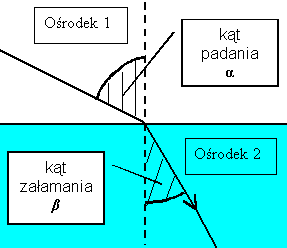
Zmiana kierunku promieni świetlnych podczas załamania nie jest przypadkowa. Opisuje to prawo załamania światła nazywane niekiedy prawem Snelliusa. Prawo załamania światła łączy ze sobą dwa kąty - kąt padania na powierzchnię rozgraniczającą dwa ośrodki i kąt załamania powstający, gdy promień przejdzie granicę i zacznie się rozchodzić w drugim ośrodku. Kąty padania i załamania są liczone od prostej prostopadłej do powierzchni, a nie od samej powierzchni.

Prawo załamania światła ma postać:
, gdzie:

- kąt padania
- kąt załamania
- prędkość światła w ośrodku 1
- prędkość światła w ośrodku 2

Powstawanie obrazów w soczewkach

Soczewką optyczną nazywamy bryłę z przezroczystego materiału, ograniczoną (przynajmniej z jednej strony) zakrzywioną powierzchnią o regularnym kształcie (najczęściej kulistą, choć bywają soczewki ograniczone powierzchniami cylindrycznymi oraz paraboloidalnymi). Ze względu na kształt soczewki optyczne dzielą się na: dwuwypukłe, dwuwklęsłe, płasko-wypukłe, płasko-wklęsłe, i wypukło-wklęsłe.

Soczewki wypukłe z materiału o współczynniku załamania większym od współczynnika załamania otaczającego je ośrodka są soczewkami skupiającymi (zwiększającymi zbieżność wiązki światła), soczewki wklęsłe są soczewkami rozpraszającymi. Jeśli współczynnik załamania otaczającego soczewkę ośrodka jest większy niż materiału, z którego wykonana jest soczewka, rzecz ma się dokładnie odwrotnie. Jeśli na soczewkę skupiającą pada wiązka promieni równoległych, po przejściu przez nią skupia się ona w punkcie, zwanym ogniskiem (w przypadku soczewki rozpraszającej w ognisku przecinają się przedłużenia promieni wychodzących). Soczewka zamienia wiązkę równoległą na wiązkę promieni zbieżnych do ogniska. Po przejściu przez ognisko wiązka staje się rozbieżna.

Podstawową wielkością charakteryzującą soczewki optyczne jest ich zdolność zbierająca (albo zdolność skupiająca) - oznaczana zwykle jako D. Zdolność skupiająca to odwrotność ogniskowej, czyli odległości ogniska soczewki od jej środka. Dla soczewek skupiających D>0, dla soczewek rozpraszających D<0. Jednostką zdolności skupiającej jest dioptria [1 dioptria = 1 1/m]. Ogniskowa soczewki wyraża się w jednostkach miary odległości [m].

W soczewkach mogą powstawać obrazy:

• Rzeczywiste, odwrócone, powiększone lub pomniejszone,

• Urojone, nieodwrócone, powiększone lub pomniejszone.

W celu wykreślenia obrazu przedmiotu otrzymanego przy użyciu cienkiej soczewki, rysujemy dwa promienie:

• Promień nieulegający załamaniu, przechodzący przez geometryczny środek soczewki,

• Promień równoległy do głównej osi soczewki, który po załamaniu w soczewce przechodzi przez ognisko.

Równanie soczewki

Wartość ogniskowej wyraża się wzorem:

,

Gdzie:

f - ogniskowa soczewki,

x, y - odległość przedmiotu i obrazu od soczewki.

Równanie soczewki
możemy też zapisać w inny sposób. Przekształcając je, otrzymujemy
.

Można również wyrazić zależność między ogniskową f soczewki, a jej promieniami krzywizny r₁ i r₂ oraz współczynnikami załamania soczewki n i ośrodka otaczającego soczewkę n′:

.

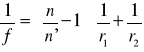
Zgodnie z tą zależnością ogniskowa soczewki zależy od współczynników załamania n i n′, a więc zmienia się zdolność skupiająca soczewki. Gdy n′>n z soczewki skupiającej otrzymuje się soczewkę rozpraszającą.

Definicja współczynnika powiększenia obrazu

Powiększeniem nazywamy stosunek wielkości obrazu do przedmiotu i oznaczamy literą M.

Wartości powiększenia oraz typ obrazu w zależności od typu soczewki i umiejscowienia przedmiotu dla soczewki skupiającej przedstawia tabela:

x	y	M
	f	0	Wiązka promieni równoległych zostaje skupiona w ognisku
> 2f	f < y < 2f	< 1	Obraz rzeczywisty, zmniejszony, odwrócony
2f	2f	1	Obraz rzeczywisty, naturalnej wielkości, odwrócony
f < x < 2f	> 2f	> 1	Obraz rzeczywisty, powiększony, odwrócony
f			Promienie z ogniska tworzą po odbiciu od zwierciadła wiązkę równoległa
0 < x < f	< 0	< -1	Obraz pozorny, powiększony, prosty
< 0	0 < y < f	-1 < M < 0	Obraz rzeczywisty pozornego przedmiotu, zmniejszony, prosty

Wartości powiększenia oraz typ obrazu w zależności od typu soczewki i umiejscowienia przedmiotu dla soczewki rozpraszającej przedstawia tabela:

x	y	M
> 0	- f < y < 0	1 < M < 0	Obraz pozorny przedmiotu rzeczywistego, zmniejszony, prosty
-f < x < 0	> 0	M < -1	Obraz rzeczywisty przedmiotu pozornego, powiększony, prosty
- f			Wiązka promieni zbieżnych do ogniska pop przejściu przez soczewkę staje się równoległa
-2f < x < -f	< -2f	> 1	Obraz pozorny przedmiotu pozornego, powiększony, odwrócony
- 2f	- 2f	1	Obraz pozorny, odwrócony, wielkości przedmiotu pozornego
< -2f	-2f < y < -f	< -1	Obraz pozorny przedmiotu pozornego, zmniejszony, odwrócony
	- f	0	Wiązka promieni równoległych do osi optycznej staje się po przejściu przez soczewkę rozbieżna.

Wartość ogniskowej soczewki wyznaczanej metodą Bessela:

przy założeniu, że e > 4f, gdzie: e - odległość między przedmiotem a ekranem, odległość między położeniami soczewki.

Tabela pomiarowa:

e			a
[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]

II. Wykonanie ćwiczenia:

1. Ustawiono układ pomiarowy jak na rys. 2, 3, odczytano ze skali odległość e pomiędzy przedmiotem P, a ekranem E.

• 
  
  

• 
  

2. Przesunięto soczewkę w kierunku ekranu znajdując takie jej położenie
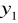
   , aby na ekranie widoczny był ostry powiększony obraz przedmiotu. Zmierzono również wysokość powstałego obrazu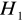
   .

3. Przesunięto soczewkę w kierunku ekranu przy nie zmienionym e znaleziono jej położenie
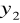
   takie, że na ekranie powstał ostry pomniejszony obraz przedmiotu. Zmierzono wysokość powstałego przedmiotu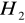
   .

4. Czynności z punktów 2 i 3 powtórzono 10 razy.

5. Obliczono ogniskową soczewki z zależności:
   .

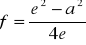
6. Obliczono wysokość przedmiotu korzystając z zależności:
   

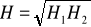
7. Obliczono wartość średnią
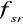
   i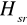
   .

8. Obliczono wartości średnie z
   

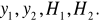
9. Oszacowano błędy pomiarowe
   .

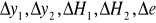
III. Obliczenia

Obliczono ogniskową soczewki dla poszczególnych pomiarów:

Obliczono wysokość przedmiotu:

Obliczono średnią wartość ogniskowej soczewki:

= 200,51

Obliczono średnią wartość wysokości przedmiotu:

= 7,36

Obliczono wartości średnie z:

= 530,5

= 328,7

= 11,6

= 4,7

Oszacowano błędy pomiarowe
, licząc je jako średnie kwadratowe średniej arytmetycznej.

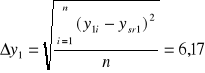
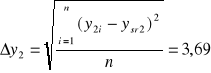
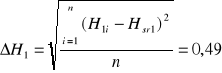
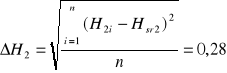
Jako
przyjęto 0,5 cm.

6

---