Kamil Gdula 20.03.2006

Sprawozdanie z ćwiczenia nr 21

Rozładowanie kondensatora

1. Zagadnienia teoretyczne:

Pojemnością elektryczną odosobnionego przewodnika nazywamy wielkość fizyczna C równą stosunkowi ładunku q zgromadzonego na przewodniku do potencjału
tego przewodnika.

Odosbniony przewodnik znajduje się w tak dużej odległości od innych ciał, że wpływ ich pola elektrycznego jest pomijalny.

Pojemność wzajemna dwóch naładowanych przewodników, zawierających ładunki q i -q wynosi:

gdzie
i
to potencjały tych przewodników.

Rodzaje kondensatorów

- Ceramiczne - mają niewielką pojemność 1-1000pF i dobre parametry elektryczne
- Ferroelektryczne - osiągają trochę większe pojemności 1-100nF, z wyglądu przypominają ceramiczne, jednak są mało dokładne i ich pojemność zależy znacznie od temperatury
- Monolityczne - posiadają kształt prostopadłościanu, osiągają niewielkie pojemności 100pF-1nF i posiadają dobre parametry elektryczne, ale są drogie
- Mikowe - bardzo zbliżone właściwości do ceramicznych, ale produkowane w szerszym zakresie 33pF-10nF
- Zwijane - dwa paski folii aluminiowej zawija się i rozdziela warstwą izolacyjną. Produkowane są w szerokim zakresie 10pF-10uF, dzielą się na:
  - papierowe - już nie stosowane
  - styrofleksowe - oznaczenie KSF
  - poliestrowe - oznaczenie KSE

Odmianą kondensatorów KSE są MKSE, które posiadają mniejsze wymiary od KSE.
- Elektrolityczne - osiągają bardzo duże pojemności w stosunku do gabarytu w zakresie 1uF do nieskończoności (zależnie od techniki), posiadają duże wahania pojemności i są wrażliwe na zmiany temperatury (w szczególności poniżej temp. 273K).

Ładowanie kondensatora odbywa sie w układzie jak na rys. 1.

W chwili początkowej, tzn. dla t = 0 napięcie na kondensatorze U_C = 0 .

Po upływie czasu t ładunek zgromadzony na okładce kondensatora można wyrazić

zależnością:

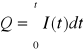
a napięcie między okładkami kondensatora:

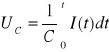
Napięcie źródła możemy wyznaczyć z zależności:

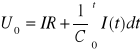
Z zależności tej po przekształceniach otrzymujemy wyrażenie na prąd ładowania kondensatora:

Napięcie między okładkami kondensatora w czasie ładowania przyjmuję postać:

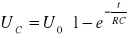
Wielkość RC nazywa się stałą czasową obwodu RC   .

Można zauważyć, że dla   t prąd ładowania maleje e-krotnie (e - podstawa

logarytmu naturalnego).

Rozładowanie kondensatora odbywa się w obwodzie jak na rys.2

W chwili początkowej t = 0 napięcie na kondensatorze wynosi U₀ i wyrazi się wzorem:

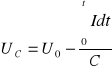
Zgodnie z II prawem Kirchoffa możemy zapisać, że:

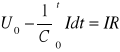
Prąd rozładowania wyraża się taką samą zależnością jak prąd ładowania, czyli:

a napięcie między okładkami kondensatora w trakcie rozładowania, możemy wyliczyć z zależności:

Przedstawiając zależność na prąd ładowania(rozładowania) w postaci:

jest ona korzystna do obliczania stałej czasowej obwodu, a wykres
jest prostą przechodzącą przez początek układu współrzędnych. Współczynnik kierunkowy tej prostej jest równy odwrotności stałej czasowej obwodu.

2. Wykonanie ćwiczenia:

1. Połączyć obwód wg schematu

Rys. 5. Schemat obwodu do badania rozładowania kondensatora: 1, 2 pozycja przełcznika K

2. Naładować kondensator (przełącznik K w pozycji 1). Ustawić taką wartość oporu R,

aby natężenie prądu było maksymalne, (I = I₀ dla t = 0s).

3. Przełączyć przełącznik K w pozycję 2 i jednocześnie włączyć sekundomierz. Przeprowadzić pomiary natężenia prądu rozładowania kondensatora I = f(t).

4. Sporządzić wykres zależności prądu rozładowania I = f(t) oraz wykres

5. Wartość ładunku zgromadzonego na okładkach kondensatora obliczyć wyznaczając

wartość pola powierzchni zawartego między osiami współrzędnych a wykresem I = (t).

6. Wyznaczyć pojemność kondensatora:

gdzie: Q - wartość ładunku zgromadzonego na okładkach kondensatora,

U - napięcie między okładkami, które w tym przypadku jest równe napięciu

zasilającemu obwód pomiarowy.

7. Obliczyć stałą czasową obwodu: a) na podstawie wykresu I(t) korzystając z definicji

stałej czasowej, b) z zależności RC   , c) korzystając z wykresu

poprzez wyznaczenie współczynnika kierunkowego tej prostej. Przedyskutować otrzymane wyniki.

Tabela pomiarowa

U	R	I0	t	I	Q	C	τ
[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]

---