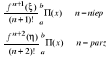Zadanie numeryczne, uwarunkowanie zadania numerycznego; wskaźnik uwarunkowania, przykłady:
Zadanie numeryczne: ϕ : D⊂Rn → Rm
d (wektor danych = [d1…dn]), ~d(zaburzenie) ∈ D
ω (wektor wyników) ∈ Rm (∈ϕ(d))
Algorytm - A(d) ≠ ϕ(d) (może być zaokrąglenie)
Wskaźnik uwarunkowania: cond(d)<1 dobrze uw.
![]()
Dla funkcji :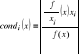
Sposoby reprezentacji liczb w maszynie cyfrowej, arytmetyka zmiennopozycyjna fl, własności ar. fl:
x=s*2c*m, s∈{±1}, c∈Ζ, m-mantysa m∈[½, 1),
m=Σe-i2-i, e-1=1, e-1∈{0,1}
mt=Σe-t2-t +e-(t+1)2-t - praw. zaokr.
|x-rd(x)|=2c|m-mt|≤½2c-t
rd(x)=x(1+δ), | δ|≤2-t
fl(a□b)=rd(a□b), fl2=t:=2l (Algorytm Gilla-Mǖlera: sumow. z uwzględ. popraw.)
Algorytm metody numerycznej, numeryczne stabilności algorytmu, błąd algorytm. num. stabilnego, przykłady:
Algorytm jest numerycznie stabilny ⇔ ∃K (niezal. od arytmet. i cond(d)), że ∀d∈D ∃~d ||d-~d|| ≤ k2-t||d|| oraz fl(A(d)) = ϕ(~d)
Błąd algorytmu: ||fl(A(d))- ϕ(d)|| = ||ϕ(~d)- ϕ(d)|| ≤ cond(d)![]()
||ϕ(d)|| ≤ Kcond(d)2-t||ϕ(d)||
![]()
≤ K cond(d)2-t
Normy wektorów i macierzy oraz ich własności:
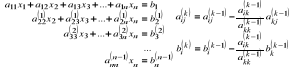
Wektorów: Normy Höldera: ||x||p=limp∞||x||p=![]()
p ≥1; euklidesowa: pε{1;2}; ||x||2=![]()
||x||∞=maxi|xi|
||x||∞ ≤ ||x||2 ≤ ||x||1 ≤ √(n)||x||2; ||x||1 ≤ n||x||∞; ||x||2 ≤ √(n)||x||∞
Macierzy: Euklidesowa (Shuma): ||A||E=![]()
; Indukowana: ||A||p=![]()
||A||1=maxj ∑i|aij| kolumnowa; ||A||2=maxλεSp√λ spektralna; ||A||∞maxi ∑j|aij|; ||Ax||*≤||A||^ ||x||* zg.z norm.w.
Własności: ||AH||2=||A||2; ||AHA||2=||A||22; ||A||22 ≤ ||A||1 ||A||∞; ||AB||p ≤ ||A||p ||B||p
A unitarna: ||A||2=1; ||AB||E = ||B||E;
||BA||E = ||B||E; W hermit: ||A||2 = maxλ|λ|
Macierze L(k) i macierze permutacji, ich własności i zastosowanie:
Macierz PεRnxm nazywamy macierzą permutacji, jeżeli ∀i ∑j pij=1 oraz ∀j ∑i pij=1; pijε{0,1}
Własności: PT=P-1 (ortogon); det(P)=sgnσ; PTA -przest. wierszy; AP -przest. kol.; Pkl= PklT= Pkl-1
Własności L(k): det L(k)=1; (L(k))-1-bez minusów; L(1) L(2)… L(k)-trójkątna diag(A)=1, -lij; Niech a=[a1…an]T lik=ai/ak;
Zadanie rozwiązywania układów równań liniowych, wskaźnik uwarunkowania, rozwiązywanie układów z macierzami trójkątnymi:
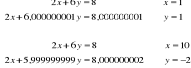
~A=A+δA (macierz zaburzeń) ~b=b+δb (wekt. zab)
~x=x+δx - zaburzenie wyniku; cond(A) wskaź. uw.
![]()
; cond(A)=||A|| ||A-1||
Twierdzenia:
||A-1 δA||<1 => det(~A)≠0
||A-1 δA||≤ε<1 => ![]()
||I||=||AA-1||≤||A|| ||A-1||=cond(A) => condp(A) ≥ 1 AT=A-1 (ortogon.) => ||A||2=1 i ||A-1||=1 - zad. dobrze uw.; A=AT => ||A||2=maxλ|λ| i ||A-1||=1/minλ|λ| => cond2(A)=||A||2 / ||A-1||
Macierz Hilberta: ![]()
-źle uwarunkowana
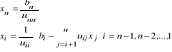
Mać. trójkątne:
diag(A)≠0
num.stab<=> K≈n
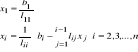
1. górna
2. dolna
koszt:
(*) 0+1+…+(n-1); (+) 0+1+…+(n-1); =½ n(n-1)
Metoda el. Gaussa rozw. układów równań liniowych, rozkład LU, częściowy i pełny wybór elem. głównego
Gauss: li1=ai1 / a11 Koszt: (*) n3/3; (+) n3/3
![]()
Rozkład LU . 2 układy z mać trójkątną, koszt (2 ½ n2)
Doolittle'a − ![]()
Crouta − ![]()
Cholesky'ego − ![]()
U=A(n)=L(n-1)A(n-1)L(n-1)…L(1)
Wybór elementu głównego (częściowy) ![]()
Zamieniamy także kol. mać. b
Wybór elementu głównego (pełny) ![]()
Rozkład trójkątny z wyb. część. A=P1,p1(L(1))-1 P2,p2(L(2))-1 … P(n-1),p(n-1) (L(n-1))-1 U
Rozkład trójkątny z wyb. pełnym A(k+1)=L(k)Pk,pk A(k) Pk,qk (zamiana i kolumn i wierszy)
Macierz diagonalnie silnie dominująca: ![]()
Metoda eliminacji Gaussa rozwiązywania ukł. równ. dla mać. 3diag i pasmowych
A=LU, gdzie L: diag(L)=1 i w dół β2… oraz U: diag(U)=α1 i w bok c1… α1=1; βi=bi / α1-i; αi=ai - βici-1
(a1 an bi ci) ≠ 0 oraz |ai|≥|bi|+|ci| przy czym przynajmniej 1 z tych nierówności jest ostra to układ Ax=f ma jednoznaczne rozw. i jest numerycznie stabilny.
k:=1…n-1 //szerokość w=p+q+1
p1=min(p+q,n-k); q1=min(q,n-k); //wybór el. głównego i zam wierszy
r: max =|aik(k)|=maxk<i<k+q1|aik(k)|
max=0 => STOP
zamień arj(k) ⇔ akj(k) j=k…k+p1 br(k) ⇔ bk(k)
for i=k+1…k+q1 //eliminacja
l=aik(k) / akk(k)
aij(k+1)=aij(k) - lakj(k) j=k+1…k+p1
bi(k+1)=bi(k) - lbk(k)
k=n…1
p1=min(p+q,n-k) xk = (bk(k)-∑j=k+1…k+p1akj(k)xj) / akk(k)
Koszt nqw [(*)(+)]
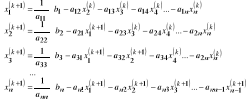
Metoda Banachiewicza (dla macierzy rzecz. i symetrycznych i dodatnio określonych) rozwiązywania układów równań liniowych, rozkład A=LLT
Własności: A=AT>0 =>: ∃α>0 (axx) ≥α||x||22; det(a)>0; Sp(A)⊂R+
Tw. ![]()
Tw. Sylwestra A=AT => A>0 wszystkie minory główne są dodatnie
dla j=1…n: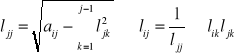
koszt n3/6
Odwracanie macierzy i obliczanie wyznaczników
A=LU lub A=LLT lub A=QR to A-1 = U-1L-1 = L-1TL-1 = R-1Q-1 = R-1D-1QT
uii≠0≠lii, W=U-1, S=L-1
i:=1…n
wii=1/uii sii=1/lii
wij= (∑k=i…j-1wikuik)/ujj j:=i+1…n
sij=-(∑k=j…i-1likskj)/lii j=1…i-1
detA = detLdetU = ∏liiuii = ∏lii2 = detQdetR = ±∏√(|di|) rii
Metoda iteracji prostej rzwiązywania układów równań liniowych, ogólny warunek zbieżności, sposoby przejścia z układu Ax=b do x=Bx+c
ρ(B)=maxλ|λ| =(dla dow mać.) limkk√||Bk||2 - promień spektralny macierzy B
x(k+1)=Bx(k)+c; x(k)x*; ciąg x(k)jest zbieżny przy dowolnym x(0) jeżeli ρ(B) <1 (im mniej tym szybciej)
x(k+1)- x* = B(x(k)-x*) =…= Bk+1(x(0)-x*) => x(k)-x* = Bk(x(0)-x*) => ||x(k)-x*||2 ≤ ||Bk||2 ||x(0)-x*||2 ||Bk||2≈[ρ(B)]k
Metoda Richardsona:
Ax=B pAx=pB (p≠0) x=x-pAx+pb x=(I-pA)x + pb = BR + CR
A=AT>0 to ρ(BR) = maxSp(BR)|μ| = maxSp(A)|1-pλ| = max((|1-pλmin|, |1-pλmax|) => pε(0, 2/λmax); popt=2/(λmin+λmax)
![]()
i dla dużych cond(A) wolna zbieżność
xi(k+1) = xi(k) + p(bi-∑jaijxj(k)), k=0…n
redukowalna: ∃P: PTAP=![]()
silnie/słabo dominująca: |aii|≥∑i≠j|aij|; sil.: wszystkie >, sł.: przyn. 1;
Metody Jakobiego i Seidla j/w
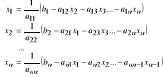
Jakobi:
A=L+D+U =
▲+ \ +▼,
Aii≠0; …
Dx = -(L+u)x + b x= -D-1(L+U)x+ D-1b = BJx + CJ
xi(k+1) = (bi - ∑j≠iaijxj(k))/aii i=1…n; k=0…;
zbieżna: A silnie dom., A słabo dom. i niereduk.
Gauss - Seidl:
x = -(L+D)-1Ux + (L+D)-1b = BGSx + CGS
xi(k+1) = xi(k) +
+ (bi - ∑j<i-1aijxj(k+1) - ∑i-1<j<n+1aijxj(k))/aii
zbieżna: słabo dom. i niereduk., A=AT>0
Metoda SOR j/w
w=1GS
Bw = (d+wL)-1((1-w)D-wU); Cw = w(D+wL)-1b
xi(k+1) = xi(k) + w(bi - ∑j<i-1aijxj(k+1) - ∑i-1<j<n+1aijxj(k))/aii
zbieżna: A=AT>0 to ∀wε(0,2) ρ(Bw)≥|w-1|
Porównanie metod iteracji prostej dla układów równań liniowych z macierzą symetryczną i dodatnio określoną oraz posiadającą własność A
A ma własność A jeżeli istnieje P: PTAP=![]()
, gdzie D1, D2 macierze diagonalne
Tw. Jeżeli A=L+I+U A=AT>0 i nie ma własności A to
ρ(BJ)=ρ(BR)|p opt
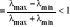
ρ(BGS)=ρ2(BJ)
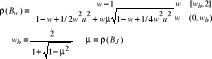
wb jest optymalne
Więc λmax≠λmin => 0 < ρ(Bw opt) < ρ(BGS) < ρ(BR)|p opt <1
ρ(BR)|p opt = ρ(BJ) = ![]()
ρ(Bw opt) = wopt-1 = ![]()
Tw. Gerszgorina; Sp(A) ⊂ ∪Ki(aii, rii) = ∑j≠i|aij|
Zadanie interpolacji wielomianowej funkcji jednej zmiennej, błąd interpolacji, wielomian interpolacyjny Lagrange'a:
Zadanie: Danych jest n+1 węzów ![]()
i klasa funkcji G, szukamy takiego![]()
aby ![]()
Jednoznaczność: ![]()
posiada conajw. n+1 pierw
Błąd: |Π(x)| = |(x-x0)… (x-xn)| ≤ ¼n!hn+1; h=maxi(xi-xi-1);
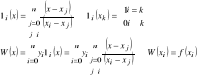
Tw. f∈Cn+1[a,b] => ∀x∈[a,b] ∃ξ∈[a,b] że R(x) = f(x) - w(x) =![]()
R(x) = |f(x) - w(x)| ≤ … ![]()
Lagrange:
Zadanie interpolacji wielomianowej funkcji jednej zmiennej, błąd interpolacji, wielomian interpolacyjny Newtona:
fi=f(xi); fij=(fi-fj)/(xi-xj);
fi…i+k = (fi…i+k-1 - fi+1…i+k) / (xi - xi+k)
![]()
węzły równoodległe: xi=a+ih; h=|a-b|/n
Zadanie interpolacji wielomianowej funkcji jednej zmiennej, optymalny wybór węzłów - węzły Czybyszewa
Chcemy aby zminimalizować maxx|Π(x)|
x= ½[(b-a)t+(a+b)], t∈[-1;1]; ![]()
![]()
wzór rekur.
Wtedy |R(x)|≤![]()
Jak interpolujemy |x| albo 1/(1+25x2) to efekt Rungego
Zadanie interpolacji wielomianowej funkcji jednej zmiennej, klasyczna interpolacja Hermita:
∑imi:=n+1, m=max(mi) (wyrównujemy również pochodną) wj(xi)=f(j)(xi), j=0…mi-1; Dla m=2 klasyczna, m=1 Lagrange
Błąd klasycznej: R(x) = Π(x) (f(2n+2)(ξ)) / (2n+2)!; Π(x)=(x-x0)m0…(x-xn)mk=(x-x0)2…(x-xn)2
Klasyczna: 0…n węzłów, W2n+1;
ϕi:=[1-2(x-xi)l`i(xi)]l2i(x) ϕi(xk) = ψ`i(xk)=δik
ψi:=(x-xi)l2i(x) ϕ`i(xk) = ψi(xk)=0
W(x)=∑f(xi)ϕ(x) + ∑f`(xi)ψ(x)
Sposoby numerycznego różniczkowania
f(j)(x) ≈ w(j)(x); Tw: f∈Cn+1[a,b] to max|f(j)(x) - w(j)(x)|≤![]()
f'(x)≈(f(x+h)-f(x))/h
f'(x)≈(f(x)-f(x-h))/h r(x)=f`(x)-[f'(x)h + ½ f''(ζ)h2]/h = ½hf''(ζ)
f'(x)≈(f(x+h)-f(x-h)) / 2h
f'(x)≈(f(x+h)-2f(x)+f(x-h)) / h2
Całkowanie funkcji jednej zmiennej - formuły proste Newtona - Cotesa (prostokątów, trapezów, Simpsona)
S(f) = ∑Aif(xi) Ai-współcz. form.; r(f)=I(f)-S(f)
NC: xi=a+ih; h=(b-a)/n; S(f) = ∫abw(x)dx
n |
|
nazwa |
wzór |
|
reszta kwadratury |
kwadratury |
|
0 |
Dla n≥1 |
prostokątów |
(b-a)f(x0) = hf(x0) |
1 |
(12) |
trapezów |
(b-a)[f(a)+f(b)]/2 |
2 |
(2880) |
Simpsona |
(b-a)… [f(a)+4f(x1)+f(b)]/6 |
3 |
(6480) |
3/8 |
(b-a)… …[f(a)+3f(x1)+3f(x2)+f(b)]/8 |
Całkowanie funkcji jednej zmiennej - formuły złożone Newtona - Cotesa (prostokątów, trapezów, Simpsona)
I(f) = ∫abf(x)dx = ∑∫xi-1xif(x)dx ≈ ∑Si(f) = S(f)
r(f) = ∑ri(f)
Prostokąt: S(f) = h∑f(xi(0))
xi(0)=(xi-1+xi)/2 - p.środk. |r(f)|=∑(f(2)(ξi) h3) / 24
mm2 ≤ ∑f(2)(ξi) ≤ M2m => minx(f2(x)) ≤ (∑f(2)(ξi)) / m ≤ maxx(f2(x)) => r(f) = (f(2)(ξ) h2)(b-a) / 24
|r(f)| ≤ M2h2(b-a) / 24
Trapez : S(f) = ½h[f(a) + f(b) + 2∑f(a+ih)]
Simpson: S(f) = h[f(a) + f(b) + 2∑f(a+ih) + 4∑f(a+ih-h/2)]/6
Rozwiązywanie równań nieliniowych, wykładnik zbieżności, sposoby lokalizacji pierwiastków:
f[a,b]R, szukamy f(x*)=0
- tablicowanie (wykres) - f(a)f(b)<0 => ∃x* oraz f'(x) ma stały znak to ∃! - graficznie f(x)=f1(x) - f2(x)
Met. int. jest rzędu p (p≥1) jeżeli istnieje A>0, że ciąg x(k) określony tą metodą spełnia nierówność: |x(k+1)-x*| ≤ A|x(k)-x*|p {dobre: A małe, p duże}
p=1 zbieżność liniowa |x(k+1)-x*| ≤ A|x(k)-x*| ≤ |x(k+1)-x*| ≤ A2|x(k-1)-x*| ≤…≤ Ak+1|x(0)-x*|; A<1 - war. zbież.
p>1 zbieżność ponadliń. |x(k+1)-x*| ≤ (A1/(p-1)|x(0)-x*|)pk-1|x(0)-x*|; A1/(p-1)|x(0)-x*|<1 - war. zbież.
Metody rozwiązywania skalarnych równań nieliniowych, ich własności i porównanie:
Metoda stycznych poszukiwania pierwiastków równania skalarnego, wykładnik zbieżności i warunki zbieżności metody:
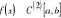
;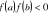
;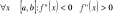
.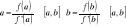
Metoda iteracji prostej rozwiązywania układu równań nieliniowych, wykładnik zbieżności i warunki zbieżności:
Metoda Newtona rozwiązywania układu równań nieliniowych, wykładnik zbieżności i warunki zbieżności:
Metody rozwiązywania równań skalarnych posiadających zera wielokrotne:
Metody poszukiwania zer wielomianów:
Interpolacja trygonometryczna:
Nazwa |
p/A |
założenia |
zbieżność |
wzór |
bisekcja |
1 A=½ |
ciągła [a,b] |
bezwrunk. |
x1= ½(a+b); f(xi)f(a)<0 to [a,xi] k-ty: (b-a) /2k<ε |
styczne |
2 A=M2/2m1 |
kl.C2[a,b] |
warunk. |
x(k+1) = x(k) - f(xk)/f1(xk) |
sieczne |
½(1+√5)≈1,6 A=(M2/2m1)p |
kl.C2[a,b] |
warunk. |
x(k+1) = x(k) - [f(xk) / (f(xk) - f(xk-1)] (xk-xk-1) |
regulafalsi |
1 |
kl. C[a,b] |
|
miejsce przecięcia odcinka ab, itd. |
Steffensena |
2 |
|
|
xk+1 = xk - f2(xk) / [f(xk+f(xk)) - f(xk)] |
Halleya |
3 |
|
|
xk+1 = xk - [f(xk) f1(xk)] / [f1(xk)- ½f(xk) f2(xk)] |
it. prostej |
1 |
|
M1<1 |
xk+1 = g(xk) |
x0∈[a,b] =![]()
![]()
f1(x0) = tgα = f(x0)/(x0-x1)
Zbieżność globalna dla dowolnego ![]()
- jeżeli
Kryteria STOPU: ![]()
|x* - xk|<|f(xk)|/m1
x0-przyliżenie początkowe; xk+1 = g(xk)
Tw1: D - zbiór domknięty => warunek Lipschitza, ponadto x*∈D to: ∃!x*; ||xk-x*||0; ||xk+1-x*||≤L||xk-x*||; ||xk-x*|| ≤ (Lk/(1-L))||x1-x0||
!!!D-zb. wypukły g(x')-g(x'')=g'(ξ)(x'-x''); g'(x) - mać. Jakobiego {δgi/δxj}i,j=1n; ||g(x')-g(x'')||=||g'(ξ)|| ||(x'-x'')|| (n.mać. zg. z n.w) wystarczy żeby L=supx||g'(x)||<1
Tw2: D-domk. i L, ∃x*, x0∈S={x: ||x-x*|| ≤ r} to xkεS i spełniona teza Tw1
xk+1=xk - [f1(xk)]-1f(xk);
Niech D-wypukły i f-różniczkowalne, oraz ∃x*, det(f1(x*))≠0, L, x0∈S to: Met. poprawnie określona; ||xk+1-x*|| ≤ q||xk-x*||; ||xk+1-x*||0; ||xk+1-x*|| ≤ (q/r)||xk-x*||2
Warunki STOPU: podobne jak it. pr. oraz ||xk+1-x*|| ≤ q||xk-x*|| ≤… ≤qk+1r ≤ε
f(x)=(x-x*)mg(x)≠0; fm(x*)=0; => p=1!!!
Alg1: F(x)=f(x)/f1(x) {x* - zero 1-krotne F}; ![]()
styczne: ![]()
p=2 (m zgadujemy )
1 zero: Newton/styczne (w pewnym otoczeniu zbieżna, p=2), sieczne, Laguerre: xk+1=![]()
znak, żeby |xk+1-xk| było mniejsze, H(x)=[(n-1)(f1(x))]2 - nf(x)f2(x), jak zbieżne to p=3; Jak n rzeczywisty z n zer to zawsze zbiega do najbliższego zera.
Schemat Hornera dla f, f', f''
an= bn= cn= dn; b/c/di = b/c/di+1x + a/b/c, i=n-1…0/1/2
f(x)=b0 f'(x)=c1 f''(x)=2d2, koszt 3n[(*)(+)]
Wyznaczanie kilku zer: deflacja czynnikiem liniowym: x*, f(x)=(x-x*)Q(x), Q(x)=∑qj+1xj
Alg1: qn+1=0; qj=aj+qj+1x*; j=n…1
Alg2: q0=0; qj+1=(qj-aj)/x*; j=0…n-1, chyba że x*=0
Maehly: f(x)=(x-x1)…(x-xn), an=1; x1 z Newtona; f1(x)= (x-x2)…(x-xn), x2 z Newtona dla f1… ; f11(x)/f1(x) = (f1(x)/f(x))(xk+1/x-x1); Trzeba uważać, żeby xi(0)≠xj
Bairstow: an=1, ajεR, f(x)=Πn/2(x2-pjx-rj)(x-a); m(x,p,r)=x2-px-r; f(x)=m(x,p,r)Q(x,p,r)+q1(p,r)x+q0(p,r).
qi obliczamy dzieląc f przez m
![]()
to samo dla r
![]()
Podstawić i ![]()
[0,2π] xk=2kπ/(n+1)
tn(x)= ½a0 + ∑[aj cos(jx) + kj sin(jx)] + v ½am+1 cos[(m+1)x], gdzie dla n -parz m=n/2, v=0; dla n-niep m=(n-1)/2, v=1
Tw. dla funkcji określonej na [0,2π] ∃!x* Ponadto aj=2/(n+1) ∑f(xk)cos(jxk); bj=2/(n+1) ∑f(xk)sin(jxk)
dla dowolnego [a,b] => v=b-a (okres)
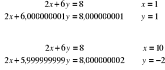
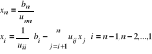
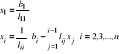
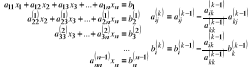
![]()
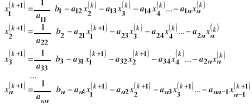
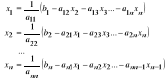
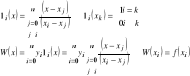
Wyszukiwarka
Podobne podstrony:
Ogólna metodologia nauk, Studia dalekowschodnie, Rok I semestr II, Metody i techniki badań społeczny
Notatki z E. Babbiego, Studia dalekowschodnie, Rok I semestr II, Metody i techniki badań społecznych
E. Babbie - Opracowanie - Paradygmaty, Studia dalekowschodnie, Rok I semestr II, Metody i techniki b
21.03.2011, Elektrotechnika I stopień PWSZ Leszno, SEMESTR II, Metody Numeryczne, 2. 21.03.2011
11.04.2011, Elektrotechnika I stopień PWSZ Leszno, SEMESTR II, Metody Numeryczne, 3. 11.04.2011
14.03.2011, Elektrotechnika I stopień PWSZ Leszno, SEMESTR II, Metody Numeryczne, 1. 14.03.2011
Mat do egzaminu 2014, Studia dalekowschodnie, Rok I semestr II, Metody i techniki badań społecznych
Litera M, Pedagogika UŚ, Licencjat 2010-2013, II rok - semestr letni, Metodyka edukacji polonistyczn
Bałwan - scenariusz, Pedagogika UŚ, Licencjat 2010-2013, II rok - semestr letni, Metodyka edukacji p
Litera O, Pedagogika UŚ, Licencjat 2010-2013, II rok - semestr letni, Metodyka edukacji polonistyczn
Plastyka, Pedagogika UŚ, Licencjat 2010-2013, II rok - semestr letni, Metodyka edukacji plastycznej
więcej podobnych podstron