Bramki logiczne
Bramka logiczna - element konstrukcyjny maszyn i mechanizmów (dziś zazwyczaj: układ scalony, choć podobne funkcje można zrealizować również za pomocą innych rozwiązań technicznych, np. hydrauliki czy pneumatyki), realizujący fizycznie pewną prostą funkcję logiczną, której argumenty (zmienne logiczne) oraz sama funkcja mogą przybierać jedną z dwóch wartości, np. 0 lub 1 (zob. algebra Boole'a).
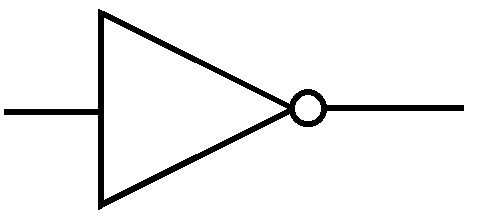
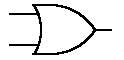
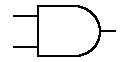
Podstawowymi elementami logicznymi, stosowanymi powszechnie w budowie układów logicznych, są elementy realizujące funkcje logiczne: sumy (alternatywy), iloczynu (koniunkcji) i negacji. Są to odpowiednio bramki OR, AND i NOT. Za pomocą dwóch takich bramek (np. OR i NOT lub AND i NOT) można zbudować układ, realizujący dowolną funkcję logiczną.
p |
Wynik |
1 |
0 |
0 |
1 |
p |
q |
Wynik |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
p |
q |
Wynik |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
p |
q |
Wynik |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
Podstawowe prawa logiczne:
I Prawo de'Morgana
p |
q |
Lewa |
~p |
~q |
Prawa |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
II Prawo de'Morgana
p |
q |
Lewa |
~p |
~q |
Prawa |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Prawo podwójnej negacji
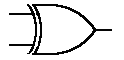
Zależność XOR od OR, AND i NOT
Wykonane ćwiczenia:
Mając do dyspozycji bramki AND oraz NOT zbuduj bramkę OR.
Mając do dyspozycji bramki OR oraz NOT zbuduj bramkę AND.
Mając do dyspozycji bramkę XOR zbuduj bramkę NOT.
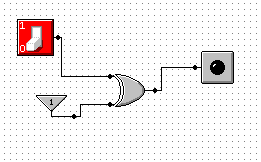
Mając do dyspozycji bramki XOR oraz AND zbuduj bramkę OR.
Mając do dyspozycji bramki XOR oraz OR zbuduj bramkę AND.
Mając do dyspozycji bramki AND, OR oraz NOT zbuduj bramkę XOR.
Zbuduj bramkę NAND korzystając z bramek AND oraz NOT.
Zbuduj bramkę NOR korzystając z bramek OR oraz NOT.
Mając do dyspozycji bramkę NAND zbuduj bramkę NOT.
Mając do dyspozycji bramkę NAND zbuduj bramkę AND.
Mając do dyspozycji bramkę NAND zbuduj bramkę OR
Mając do dyspozycji bramkę NOR zbuduj bramkę NOT.
Mając do dyspozycji bramkę NOR zbuduj bramkę OR
Mając do dyspozycji bramkę NOR zbuduj bramkę AND.
Mając do dyspozycji bramkę NAND zbuduj bramkę NOR.
Mając do dyspozycji bramkę NOR zbuduj bramkę NAND.
Mając do dyspozycji bramkę NAND zbuduj bramkę XOR.
Mając do dyspozycji bramkę NOR zbuduj bramkę XOR.
Wnioski:
p |
~p |
~(~p)) |
1 |
0 |
1 |
0 |
1 |
0 |
p |
q |
Lewa |
~p |
~q |
p^~q |
~p^q |
Prawa |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
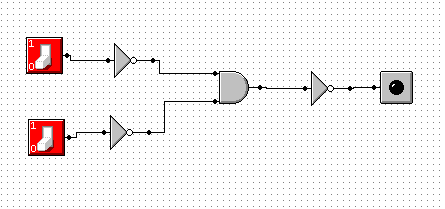
p |
q |
~p |
~q |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
Do wykonania tego ćwiczenia użyte zostało II prawo de'Morgana.
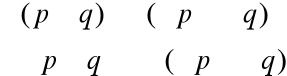
p |
q |
~p |
~q |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
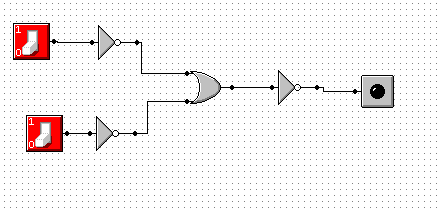
Do wykonania tego ćwiczenia użyte zostało I prawo de'Morgana
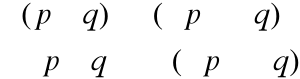
P |
„1” |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
Do wykonania tego zadania została wykorzystana zależność bramki XOR, która odwraca sygnał, gdy połączymy go ze stałą „1”
p |
q |
„1” |
~p |
~q |
~p^~q |
Wynik |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Do wykonania tego ćwiczenia użyte zostało II prawo de'Morgana oraz zależność z poprzedniego zadania, że bramka XOR odwraca sygnał, gdy połączy się go ze stałą „1”.
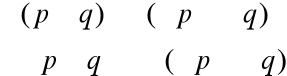
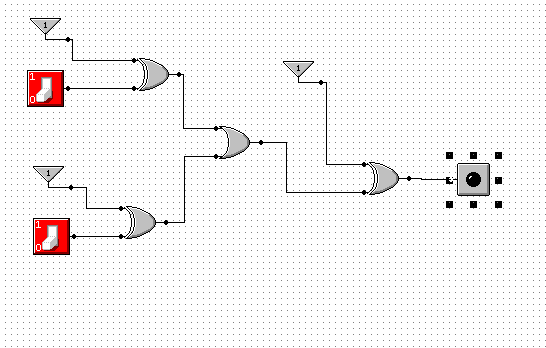
p |
q |
„1” |
~p |
~q |
~p˅~q |
Wynik |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Do wykonania tego ćwiczenia użyte zostało I prawo de'Morgana oraz zależność z zadania 3, że bramka XOR odwraca sygnał, gdy połączy się go ze stałą „1”.
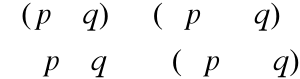
p |
q |
~p |
~q |
p^~q |
~p^q |
Wynik |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
Do wykonania tego ćwiczenia została użyta Zależność bramki XOR od bramek OR, AND i NOT
p |
q |
p^q |
Wynik |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
Przy wykonaniu tego ćwiczenia skorzystaliśmy z prostej zależności że bramka NAND, to po prostu zanegowana bramka AND
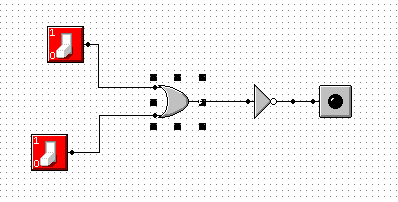
p |
q |
p˅q |
Wynik |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Przy wykonaniu tego ćwiczenia skorzystaliśmy z prostej zależności że bramka NOR, to po prostu zanegowana bramka OR
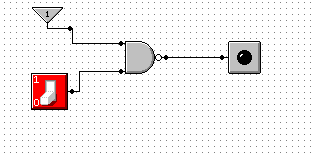
p |
„1” |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
Przy wykonaniu tego ćwiczenia korzystamy z prostej zależności że sygnał doprowadzony do bramki NAND ulega odwróceniu przy połączeniu ze stałą „1”
p |
q |
~(p^q) |
Wynik |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
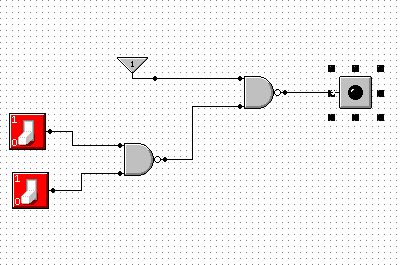
Przy wykonaniu tego ćwiczenia korzystamy z prawa podwójnej negacji dla AND, oraz z wyników ćw 9.
![]()
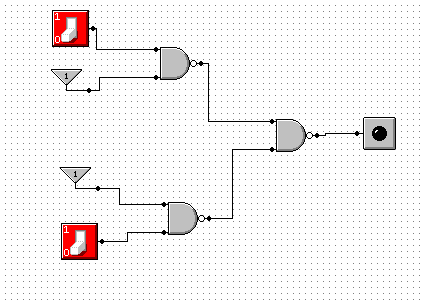
p |
q |
~p |
~q |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Przy wykonaniu tego ćwiczenia korzystaliśmy z II prawa de'Morgana oraz z wyników ćw. 9
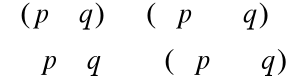
p |
„0” |
Wynik |
1 |
0 |
0 |
0 |
0 |
1 |
Przy wykonywaniu tego ćwiczenia korzystaliśmy z prostej zależności że sygnał doprowadzony do bramki NOR zostaje odwrócony gdy jest połączony ze stałym „0”.
p |
q |
~(p˅q) |
Wynik |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
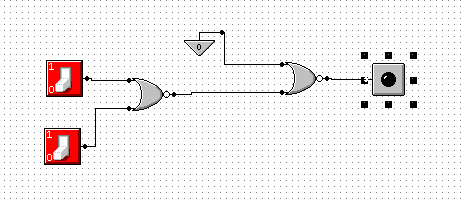
Przy wykonaniu tego ćwiczenia korzystaliśmy z prawa podwójnego zaprzeczenia oraz wyników ćw. 12.
![]()
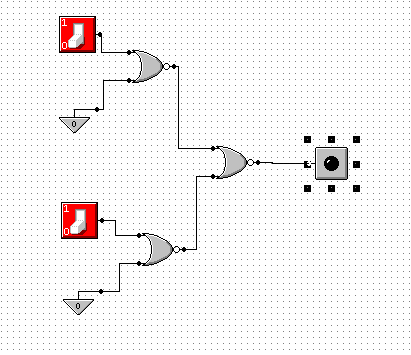
p |
q |
~p |
~q |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
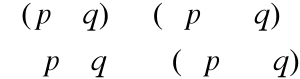
Przy wykonywaniu tego ćwiczenia korzystaliśmy z prawa I de'Morgana oraz z wyników ćw. 12
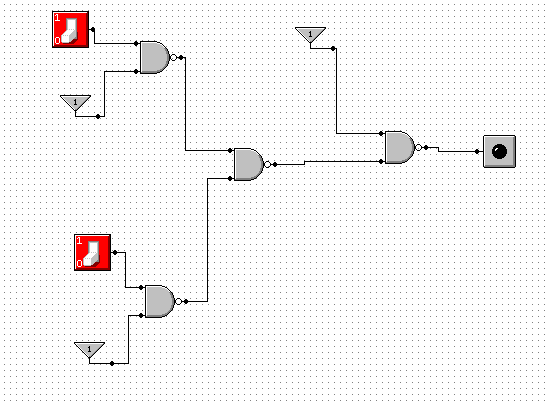
p |
q |
~p |
~q |
~(~p^~q) |
Wynik |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
Przy wykonywaniu tego ćwiczenia korzystaliśmy z II prawa de'Morgana, oraz z wyników ćw. 9 (z NAND zrobić NOT).
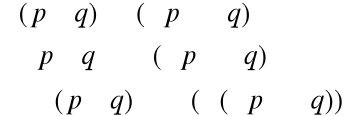
W tym przypadku nie możemy skorzystać z prawa podwójnej negacji, ponieważ musimy korzystać z bramki NAND, a gdybyśmy skorzystali z tego prawa, to po prawej stronie mamy zwykły AND.
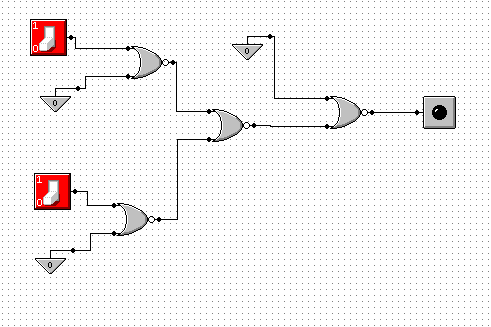
p |
q |
~p |
~q |
~(~p^~q) |
Wynik |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
Przy tym ćwiczeniu korzystamy z I prawa de'Morgana oraz z wyników ćw.12 ( z NOR zrobić NOT). Podobnie jak w poprzednim ćwiczeniu nie możemy skorzystać z prawa podwójne negacji.
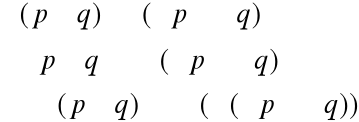
p |
q |
~p |
~q |
~(p^~q) |
~(~p^q) |
Wynik |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
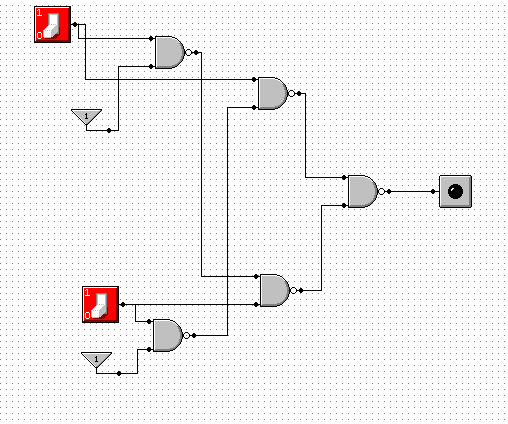
![]()
Przy wykonywaniu tego ćwiczenia korzystamy z zależności XOR, oraz z tego, że za pomocą bramki NAND możemy utworzyć NOT, AND oraz OR(ćw. 9, 10 i 11).
p |
q |
~p |
~q |
~(p˅~q) |
~(~p˅q) |
~(~(p˅~q)˅ ~(~p˅q)) |
Wynik |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
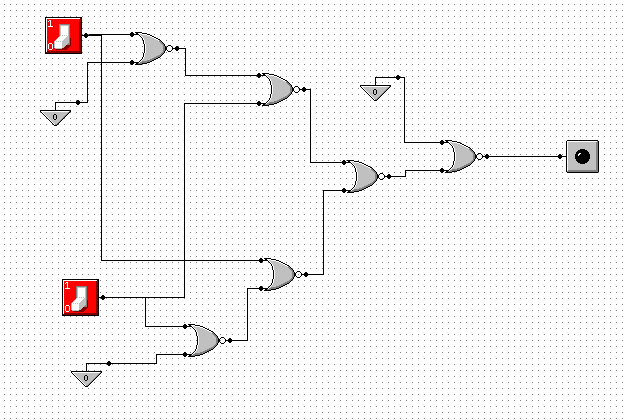
Przy wykonywaniu tego ćwiczenia ponownie skorzystaliśmy z zależności bramki XOR, oraz z tego że z bramki NOR można zrobić bramkę NOT, OR i AND (ćw.12, 13 i 14)
Ćwiczenie to nauczyło mnie, że korzystając z kilki podstawowych praw logiki, można za pomocą jednej, dowolnej bramki wykonać wiele innych bramek. Najbardziej wykazały to ćw. 17 i 18, w których za pomocą jednej bramki tworzyliśmy operacje logiczne wykonywane przez 3 inne bramki.
Bramka NOT
Bramka OR
Bramka AND
Bramka XOR
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Liczniki, stud, II semestr, PEiTC, liczniki
Liczniki2, stud, II semestr, PEiTC, liczniki2
lab07, stud, II semestr, PEiTC, liczniki
lab06, stud, II semestr, PEiTC, przerzutniki
Dioda, stud, II semestr, PEiTC, petitki
Tranzystor sprawozdanie, stud, II semestr, PEiTC, tranzystor
teoria asd, stud, II semestr, ASD
lab04, I , II semestr, PEiTC
teoria asd, stud, II semestr, ASD
Materiały do definicji i podziału logicznego, ADMINISTRACJA, I rok II semestr, Podstawy logiki prakt
Tętnice szyjne sem dla stud II
więcej podobnych podstron