11. Funkcje logarytmiczne

Niech a będzie liczbą dodatnią, różną od jedności oraz b będzie liczbą dodatnią. Logarytmem liczby b przy podstawie a nazywamy liczbę x będącą wykładnikiem potęgi, do której należy podnieść liczbę a, aby otrzymać liczbę b. A więc

Przykłady. Obliczymy logarytmy niektórych liczb.

a)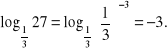

b)

c)
Czyli

d)
dla

e)

Czyli
.

Niech a, b, c będą takimi liczbami, że wszystkie wyrażenia występujące w poniższych wzorach mają sens. Prawdziwe są wówczas następujące równości:

i)

ii)

iii)

iv)

v)

Logarytmy przy postawie 10 nazywają się logarytmami dziesiętnymi i w ich zapisie pomijamy podstawę, tzn. zamiast pisać
piszemy log a.

Przykłady. Zastosujemy podane wzory do przekształcenia wybranych wyrażeń do innych postaci.

a)

Zauważmy, że lewa strona równości jest prawdziwa dla
a prawa strona wymaga mocniejszych założeń:
Cała równość jest prawdziwa oczywiście przy tych ostatnich założeniach.

b)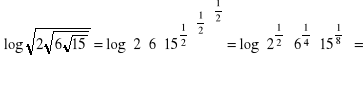

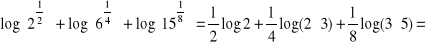
c)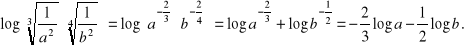

Analogicznie jak w przykładzie a), lewa strona równości jest prawdziwa dla
oraz
a prawa strona dla
oraz
Zatem cała równość zachodzi dla

d)

e)

Funkcją logarytmiczną przy postawie a, gdzie
nazywamy funkcję okreś­lo­ną wzorem

Poniżej przedstawione zostały wykresy funkcji logarytmicznych dla podstaw

oraz 

Najważniejsze własności zdefiniowanej funkcji logarytmicznej są następujące:

i) Dziedziną funkcji logarytmicznej jest zbiór liczb rzeczywistych dodatnich, tj.
W kon­sekwencji w trakcie rozwiązywania równań i nierówności logarytmicznych konieczne jest robienie zastrzeżeń odnośnie argumentów pojawiających się funkcji logarytmicznych.

ii) Zbiorem wartości funkcji logarytmicznej jest cały zbiór liczb rzeczywistych.

iii) Funkcja wykładnicza jest różnowartościowa. Oznacza to, że jeżeli
i
to
Równoważność ta jest wykorzystywana do rozwiązywania równań lo­ga­rytmicznych.

iv) Dla a > 1 funkcja logarytmiczna jest funkcją rosnącą i gdy
jest ona funkcją malejącą. W konsekwencji, jeżeli
i
to

Te z kolei równoważności mają kluczowe znaczenie dla rozwiązywania nierówności logarytmicznych.

Uwaga. Naszkicujmy w tym samym układzie współrzędnych prostą o równaniu
oraz wykresy funkcji

Jeżeli porównany wykres funkcji
z wykresem funkcji
, to zauważymy, że wykresy te są symetryczne względem osi symetrii
Sugeruje to, że funkcje f i g są względem siebie wzajemnie odwrotne. Rzeczywiście tak jest, gdyż

W ogólnym przypadku zachodzi następujący fakt:

Jeżeli
to dla funkcji
i
zachodzą zależności:

Równaniem logarytmicznym nazywamy równanie, w którym niewiadoma x występuje w wyra­żeniach logarytmowanych lub podstawach logarytmów.

Przykłady. Prześledzimy na wybranych przykładach problemy związane z rozwiązywaniem równań logarytmicznych.

a)

Rozwiązanie. Zaczynamy od zastrzeżeń:

Dla
mamy:

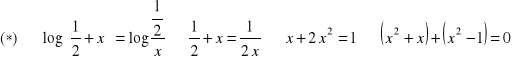
Zauważmy, że możliwość obustronnego opuszczenia znaku logarytmu, z której skorzystaliśmy, jest konsekwencją różnowartościowości funkcji logarytmicznej. Liczba
będąca drugim rozwiązaniem równania kwadratowego nie należy do dziedziny równania.

b)

Rozwiązanie. Zastrzeżenie: x > 0. Dzięki różnowartościowości funkcji logarytmicznej możemy obie strony równania
logarytmować:

Podstawiamy

Wracając do niewiadomej x mamy

Obie wyznaczone liczby należą do dziedziny równania, wiec są jego rozwiązaniami.

c)

Równanie ma sens dla wszystkich x. Mamy

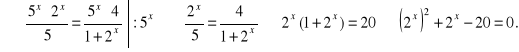
Podstawiając
otrzymujemy

Stąd
Pierwsze z równań jest sprzeczne, drugie daje rozwiązanie

d)

Rozwiązanie. Zastrzeżenia:

Otrzymaliśmy koniunkcję warunków sprzecznych ze sobą i dlatego dziedziną równania jest zbiór pusty. Równanie takie nie może mieć rozwiązań.

e)

.

Rozwiązanie. Zastrzeżenia:

Mamy dla

Rozwiązaniem równania jest liczba 6.

f)

Rozwiązanie. Zastrzeżenie: x > 0. Stosujemy wzór na zamianę podstawy logarytmu:

Znalezione rozwiązanie jest zgodne z zastrzeżeniem.

g)

.

Rozwiązanie. Muszą być spełnione warunki:

Powyższe zastrzeżenia są nieco skomplikowane, więc rozwiążemy najpierw równanie, a później sprawdzimy, czy znalezione rozwiązania je spełniają. Mamy

Łatwo stwierdzamy, że rozwiązania
faktycznie spełnia wszystkie zastrzeżenia.

h)

Rozwiązanie. Zastrzeżenia:
i
Zatem

Podstawiając
otrzymujemy

Powrót do niewiadomej x daje:

Oba znalezione rozwiązania spełniają zastrzeżenia.

Nierównością logarytmiczną nazywamy nierówność, w której niewiadoma x występuje w wy­ra­żeniach logarytmowanych lub w podstawach logarytmów.

Przykłady. Rozwiążemy serię nierówności logarytmicznych.

a)

Rozwiązanie. Zastrzeżenia:

Podstawiamy
przy czym musimy zastrzec, że
i
Wówczas

gdyż czynnik
jest stale dodatni. Stąd

Zbiorem rozwiązań jest wiec przedział

b)

.

Rozwiązanie. Zastrzeżenia:

Korzystając z faktu, że rozpatrywana funkcja logarytmiczna jest malejąca oraz, że w rozpatrywanym przedziale wrażenie
jest dodatnie, otrzymujemy dla

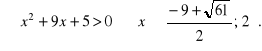
Zbiorem rozwiązań nierówności (*) jest prze­dział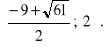

c)

Rozwiązanie. Zastrzeżenia:

Mamy

Podstawiając
otrzymujemy:

Stąd w zbiorze
otrzymujemy:

Z uwagi na zastrzeżenia stwierdzamy, że

d)

Rozwiązanie. Zastrzeżenia:

Rozwiązujemy nierówność w przedziałach składowych jej dziedziny.

1⁰
Wtedy
wobec czego

W rozpatrywanym przedziale ostatnia nierówność nie posiada rozwiązań.

2⁰
Teraz
więc

Wszystkie liczby z rozpatrywanego przedziału spełniają ostatnią nierówność.

Zbiorem rozwiązań nierówności (*) jest przedział

e)

Rozwiązanie. Zastrzeżenia:

Stosujemy wzór na zamianę podstawy logarytmu:

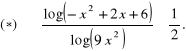
Dalej rozpatrzymy dwa przypadki.

1⁰
Wtedy
skąd

W przedziale
otrzymujemy nierówność

a w przedziale
nierówność

2⁰
Wtedy
skąd

W przedziale
otrzymujemy nierówność

a w przedziale
nierówność

W konsekwencji zbiorem rozwiązań nierówności jest suma przedziałów:

Przykłady. Wyznaczymy dziedziny funkcji.

a)

Rozwiązanie. Muszą być spełnione zastrzeżenia:

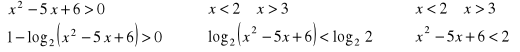
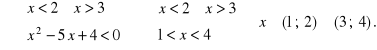
A więc

b)

Rozwiązanie. Mamy

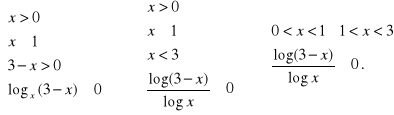
Rozpatrzymy dwa przypadki.

1⁰
Wtedy
skąd

Otrzymana nierówność końcowa nie może być spełniona w rozważanym przypadku.

2⁰
Wtedy
skąd

Zatem

Ostatecznie zachodzi równość

Rozdział 11. Funkcje logarytmiczne 80

76

y

−2

x

1

1

x

y

−4

2

4

−4

−2

2

4

x

y

---