Zaprojektować chwytak do manipulatora przemysłowego spełniającego wymagania:

• w procesie transportu urządzenie chwytające ma za zadanie pobrać (uchwycić) obiekt w położeniu początkowym, trzymać go w trakcie trwania czynności transportowych i uwolnić go w miejscu docelowym.

• obiektem transportu są wałki i tuleje o zakresie średnic d = 20÷100 mm, długości l = 20÷200 mm z mosiądzu lub stali.

• manipulator zasilany jest sprężonym powietrzem o ciśnieniu nominalnym p_n = 0,6 Mpa

Schemat kinematyczny:

1. Obliczenie ruchliwości chwytaka.

w = 3n - 2p₅ - p₄

gdzie:

n=5 -liczba członów chwytaka,

p₅=(0,1),(1,2),(1,2'),(2,3),(2',3'),(0,3),(0,3')=7 -pary kinematyczne V klasy,

p₄=0 -pary kinematyczne IV klasy,

w = 3*5 - 2*7 - 0 = 1

2. Analiza zadania projektowego i ustalenie listy wymagań:

• Wymiary transportowanego obiektu:

d = 180 [mm] - średnica największego wałka

G = 150 [N] - ciężar danego ciała

g = 9,81 [m/s²] - przyspieszenie ziemskie

n = 2 - wsp. przeciążenia chwytaka

μ = 0,3 - wsp. tarcia

2γ = 120^o - kąt nachylenia szczęk chwytaka

• Wyznaczenie maksymalnej koniecznej siły chwytu F_chmax i minimalnego wymiaru szczęki:

Układ sił działających na chwytak

a.) rozkład sił tarcia podczas chwytania obiektu

b.) rozkład sił normalnych podczas chwytania obiektu

• Wyznaczamy siły chwytu:

Dla prawidłowego uchwycenia transportowanego elementu musi być spełniony warunek:

Więc
wynosi:
[N]

• Wyznaczenie minimalnego wymiaru szczęk:

Po wstawieniu wartości liczbowych otrzymuję:

[mm]

[mm]

Szerokość szczęki a wynosi:

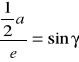
stąd
więc
[mm]

Natomiast wysokość h wynosi:

więc

Ostatecznie przyjmuje, że h = 40 [mm]

3. Wyznaczenie charakterystyki przesunięciowej chwytaka:

W celu rozwiązania zadania metodą analityczną przyjmujemy układ współrzędnych Oxy.

W schemat kinematyczny mechanizmu wpisujemy zamknięty wielobok wektorowy. Oznaczamy kąty jakie tworzą wektory z osią x układu współrzędnych. Dla przyjętego wieloboku możemy napisać równanie wektorowe:

Dane:

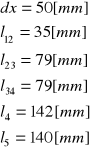
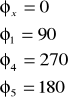
czyli

Rozwiązanie:

1.)

2.)

1.)

2.)

1.)

2.)

Podnosząc powyższy układ do kwadratu i dodając stronami mamy:

Oznaczając:

Mamy:

x² + a*x + b = 0 oraz y = l₄ - l_32*cosΦ ₃

Powyższe równania są parametrycznym równaniem charakterystyki przesunięciowej

y(Φ ₃) = f_p[x(Φ ₃)] zależnymi od kąta Φ_3.

4. Wyznaczenie charakterystyki prędkościowej chwytaka:

Charakterystykę prędkościową chwytaka otrzymujemy obliczając pochodną względem czasu.

Otrzymujemy więc:

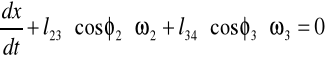
Po obróceniu układu o kąt Φ₂:

Z wyrażenia 2 wyliczamy sinϕ₂ a następnie ϕ₂ w zależności od ϕ₃ i podstawiamy do równania powyżej:

Prędkość końcówki chwytnej chwytaka:

Charakterystyka prędkościowa chwytaka:

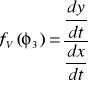
Poniżej wykres zależności prędkościowej f_v(x) (zależnej od ϕ₃ ):

5. Wyznaczenie charakterystyki siłowej chwytaka:

gdzie: F_s - siła na wyjściu zespołu napędowego (siłownika) chwytaka,

F_ch - siła chwytu (
),

f_F(x) - przełożenie siłowe mechanizmu chwytaka.

Model obliczeniowy z zaznaczonymi siłami działającymi na poszczególne człony:

Analiza sił w kolejnych grupach strukturalnych:

1. 2.

3.

Ad.1

Ad.2

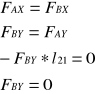
Ad.3

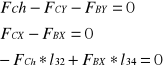
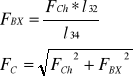
F_BX = 778.3 [N]

F_C = 890.64 [N]

Ostatecznie

F_S = 1556.6 [N]

Oraz dla położenia równowagi

f_F(x)=0.28

Sprawdzenie metodą mocy chwilowych charakterystyki siłowej chwytaka.

Bilans mocy chwilowych przy pominięciu tarcia, sił ciężkości oraz bezwładności:

N_WE + N_WY = 0

Model chwytaka do wyznaczenia bilansu mocy chwilowych

Stąd:

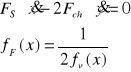
Poniżej wykres charakterystyki siłowej chwytaka f_F(x) (zależnej od ϕ₃)

6. Obliczenia wytrzymałościowe chwytaka:

Sprawdzenie warunku wytrzymałościowego na zginanie ramion chwytaka:

Maksymalny moment gnący wynosi:

M_{g max} = F_ch*l₃₂ = 61,5 [Nm]

Przyjmując przekrój prostokątny ramienia o wymiarach:

b=13[mm]

h=13[mm]

oraz materiał ramienia St6 dla którego:

obliczono

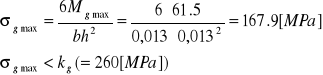
Sprawdzenie warunku wytrzymałościowego na ścinanie dla najbardziej obciążonego sworznia:

Z warunku wytrzymałościowego na ścinanie sworznia w punkcie C sprawdzono jego wytrzymałość.

Założenia:

d_s=8 [mm] - średnica sworznia

R_e=280 [MPa] - dla materiału sworznia (45)

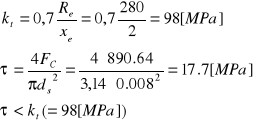
Obydwa warunki wytrzymałościowe zostały zachowane.

7. Obliczenie wymaganych parametrów napędu pneumatycznego chwytaka:

Model siłownika pneumatycznego dwustronnego działania

Siłownik dobieram zgodnie z zasadą:

gdzie:

- teoretyczna siła pchająca lub ciągnąca

- obliczona wymagana siła na tłoczysku

- współczynnik przeciążenia

- maksymalna siła na tłoczysku siłownika potrzebna do uzyskania

maksymalnej siły chwytu

W moim przypadku wymagana siła na tłoczysku wynosi:

Teoretyczną siłę pchającą lub ciągnącą obliczamy z następujących wzorów:

siła pchająca:

siła ciągnąca:

gdzie:

- ciśnienie nominalne zasilania

Zgodnie z zasadą

Wyliczamy minimalną średnicę tłoka, równą:

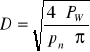
czyli minimalna średnica tłoka powinna wynosić:

Dobór siłownika z katalogu firmy FESTO

Na podstawie powyższych obliczeń wybrano odpowiedni siłownik z katalogu firmy FESTO ADVULQ-50--P-A o następujących parametrach:

Siłownik kompaktowy z bezdotykową sygnalizacją położenia, zabezpieczenie przed obrotem w postaci kwadratowego tłoczyska.

dwustronne działanie;

średnica tłoczyska: 50 [mm];

skok minimalny: 1 [mm];

skok maksymalny: 300 [mm];

ciśnienie operacyjne minimalne: 0.8 [bar];

ciśnienie operacyjne maksymalne: 10 [bar];

siła pchająca: 1178 [N];

siła ciągnąca: 1057 [N];

Do siłownika dobrano także płytkę montażową typu FUA-63.

n

p

d

D

---