Instytut Fizyki UMK Toruń, semestr letni 2011

Fizyka Atomowa i Molekularna; wykład 8, 9 i10
Andrzej J. Wojtowicz

6a. Atom wodoru i jony wodoropodobne, pełny opis

Hamiltonian układu składającego się z Z protonów i jednego elektronu, z uwzględnieniem wszystkich współrzędnych sferycznych ma postać:

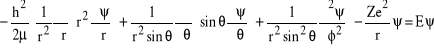
. (1)

Próbujemy rozseparować zmienne kątowe i promień wodzący, podstawiając funkcję postaci:

.

Prowadzi to do równania (1) w następującej postaci:

(2)

która wyraźnie wskazuje możliwość separacji obu stron. Wynika to stąd, że każda z nich zależy od innych zmiennych, zatem każda musi być równa tej samej stałej, zwanej stałą separacji. Oznaczymy tę stałą C. Mamy zatem:

. (3)

Jest to zupełnie ogólne równanie nie zawierające ani energii potencjalnej ani całkowitej, jego rozwiązania mogą zatem być przydatne nie tylko w przypadku atomu wodoru, czy jonów wodoropodobnych.

Postać równania (3) sugeruje możliwość dalszej separacji, o ile założymy, że funkcja:

. (4)

Podstawiając funkcję w tej postaci do równania (3) i dzieląc obie strony przez Y oraz mnożąc przez
otrzymamy:

, (5)

równanie, które znowu składa się z dwóch części zależnych od różnych zmiennych. Każda z nich musi być zatem równa tej samej stałej. Przyjmijmy, że ta stała jest równa
.

Wybierając tę ze stron równania (5), która da równanie łatwiejsze do rozwiązania, mamy następujące, bardzo dobrze znane równanie:

. (6)

Równanie (6) ma następujące rozwiązanie:

.

Rozwiązanie to będzie okresowe o ile tylko m jest dowolną liczbą całkowitą:

.

Jasne jest także dlaczego stała separacji musiała być ujemna; chodziło o to, żeby dostać rozwiązania okresowe (gdyby stała ta była dodatnia, otrzymalibyśmy niefizyczne rozwiązania monotonicznie rosnące lub malejące z kątem azymutalnym
).

Równanie na drugą, biegunową część, równania (5), będzie miało postać:

. (7)

Wprowadzając nową zmienną
i wykorzystując, że
otrzymamy:

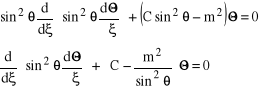
, . (8)

gdzie drugie z dwóch równań (8) otrzymaliśmy po podzieleniu pierwszego przez
.

Ostatecznie:

. (9)

Jeśli przyjmiemy, że stała
oraz, że
otrzymamy tzw. równanie różniczkowe Legendre'a:

(10)

gdzie rozwiązania tego równania, tzw. wielomiany Legendre'a, oznaczyliśmy symbolem
. Jeśli zapiszemy taki wielomian Legendre'a w postaci:

,

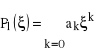
to można pokazać, że z (10) otrzymamy następujące równanie:

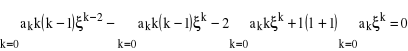
, (11)

które może się okazać przydatne dla określenia wartości współczynników
. Ponieważ pierwszy i drugi wyraz (
pierwszego członu w równaniu (11) są równe zero, możemy je pominąć w sumie i przenumerować k, podstawiając zamiast k, k + 2. Suma jest nieskończona, zatem otrzymamy:

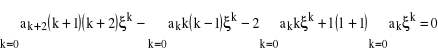
(12)

równanie, które może być spełnione tylko wtedy, gdy wyrażenia przy kolejnych potęgach
będą równe zero, co daje rekurencyjny wzór, wiążący ze sobą kolejne współczynniki
:

(13)

gdzie wszystkie współczynniki
zależą od
. Gdyby
nie było liczbą całkowitą, wielomiany Legendre'a byłyby dane szeregiem nieskończonym przy czym ich wartości dla
byłyby nieskończone, niezależnie od
. Jednak zauważmy, że jeśli przyjmiemy, że
jest naturalne, współczynniki
dla wszystkich
będą równe 0 i szereg będzie skończony. Dodatkowo musimy uwzględnić także, czy
jest parzyste czy nieparzyste; konkretnie to dla
parzystych musimy dodatkowo założyć, że
, a dla nieparzystych, że
. No i musimy także przyjąć jakieś wartości na “pierwsze” niezerowe współczynniki, czyli dla
(dla
parzystych) lub
(dla
nieparzystych). Wartości te mogą być właściwie dowolne (normujemy później pełną funkcję falową, razem z obu częściami kątowymi i częścią radialną), więc możemy je na razie dobierać tak, by wszystkie współczynniki były np. całkowite. Niżej podajemy kilka z tych wielomianów, odpowiadających kolejnym wartościom liczby
=0, 1, 2 i 3:

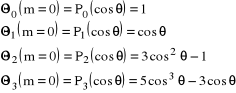
. (14)

Uciążliwe, ale właściwie nietrudne rachunki pokazują, że następujące funkcje, zwane stowarzyszonymi funkcjami Legendre'a, są rozwiązaniami pełnego równania biegunowego (9) dla m różnych od 0:

. (15)

Z postaci tych funkcji wynika, że będą one równe zeru dla
(ze względu na różniczkowanie).

Pełne rozwiązanie kątowej części równania dla atomu wodoru można wyrazić przy pomocy tzw. funkcji kulistych, zbudowanych z części azymutalnej i biegunowej. Kilka pierwszych funkcji kulistych podajemy poniżej:

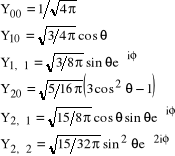
(16)

Ponieważ
, gdzie
jest liczbą naturalną, zatem dla każdej wartości
mamy
różnych funkcji kulistych.

Warto zwrócić uwagę, że część kątowa równania Schrődingera, którą zajmowaliśmy się do tej pory, a także jej rozwiązania, mają silny związek z momentem pędu. Wynika to stąd, że :

(17)

i, np. składowa z momentu pędu wyrazi się, we współrzędnych sferycznych, następującym wzorem:

(18)

a, co najważniejsze, kwadrat momentu pędu da się przedstawić w sposób następujący:

. (19)

Oznacza to, że:

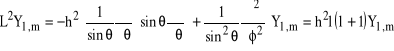
(20)

oraz, że:

(21)

czyli, że m i
są liczbami kwantowymi opisującymi moment pędu, m określa wartość rzutu momentu pędu na oś z a
wiąże się z kwadratem całkowitego momentu pędu.

Wrócimy teraz do lewej strony równania (2). Po uwzględnieniu znalezionej wartości stałej separacji C mamy:

(22)

i po małych przeróbkach, które właściwie prowadzą do wyjściowej postaci hamiltonianu, z częścią kątową zastąpioną przez odpowiednie wyrażenie, porównaj (1):

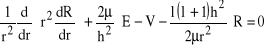
, (23)

a po wykorzystaniu innej postaci radialnej części laplasjanu:

mamy:

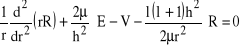
(24)

Rozwiązania równania radialnego o symetrii kulistosymetrycznej

Rozpatrzymy najpierw przypadek gdy funkcja falowa nie zależy od kątów tylko od promienia wodzącego. Oznacza to niezmienniczość układu względem obrotów, skąd wynika, że wszystkie składowe momentu pędu muszą być równe zeru, czyli, że sam moment pędu jest równy zeru, a więc
. Stany takie nazywamy “stanami s”.

Z równania (24), po podstawieniu
mamy:

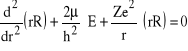
. (25)

Równanie to można znacznie uprościć, wprowadzając następujące podstawienie:
, gdzie
to promień Bohra,
, gdzie
to stała Rydberga (13,6 eV). Otrzymamy:

. (26)

Warto zauważyć, że dzięki zastosowanym podstawieniom, otrzymaliśmy równanie, w którym promień wodzący elektronu i jego energia, wyrażone są w innych, bardziej “naturalnych” jednostkach atomowych, co powoduje, że równanie jest prostsze (bez stałych).

Przyjmiemy, że
oraz przedstawimy funkcję
w postaci
(co nie stanowi żadnego ograniczenia zbioru rozwiązań, oznacza po prostu wyłączenie czynnika eksponencjalnego). Ponieważ pochodne:

oraz

a więc po podstawieniu wyliczonych pochodnych do równania (26) otrzymamy:

. (27)

Możemy wykorzystać swobodę w wyborze
(co precyzuje tylko postać wyłączonego wcześniej czynnika
) i przyjąć, że:

, (28)

wówczas równanie (27) przyjmie prostszą postać:

. (29)

Szukamy rozwiązań równania (29) w postaci szeregu potęgowego:

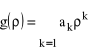
. (30)

Zanim podstawimy to wyrażenie do równania (29) warto wyliczyć pierwszą i drugą pochodną funkcji
:

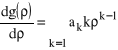
i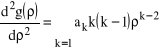
. Wstawiając te trzy wyrażenia, na funkcję
i jej pochodne, do równania (29) otrzymujemy:

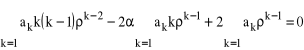
. (31)

Można zauważyć, że pierwszy składnik pierwszej sumy jest równy zeru, można zatem przenumerować całą sumę, podstawiając za k, k + 1. Pierwsza suma będzie wówczas równa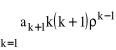
, a całe wyrażenie (31) można zapisać w następujący sposób:

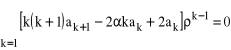
. (32)

Szereg taki będzie równy zeru, dla każdej wartości
, tylko wtedy gdy współczynniki przy wszystkich kolejnych potęgach
będą równe zero:

, (33)

dla wszystkich k, od 1 do
. Oznacza to, że:

, (34)

czyli, jeśli nadamy pierwszemu współczynnikowi,
, dowolną wartość (np. 1) to możemy wygenerować wszystkie pozostałe współczynniki wykorzystując wzór (34). W ten sposób możemy wyznaczyć rozwiązanie równania (29), dla dowolnej wartości
, czyli, poprzez zależność (28), dla dowolnej wartości
, czyli energii. Problem w tym, że takie “dowolne” rozwiązanie nie bardzo nam odpowiada, gdyż dla dużych
, czyli dla dużych k, współczynniki w szeregu potęgowym będą w przybliżeniu równe:
, co oznacza, że
. Zauważmy, że mamy wówczas (wykorzystując rozwinięcie w szereg potęgowy funkcji eksponencjalnej):

,

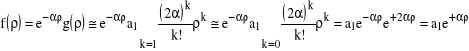
czyli, że znalezione rozwiązanie oznacza rosnące do nieskończoności prawdopodobieństwo znalezienia elektronu dla rosnącej do nieskończoności odległości elektronu od jądra. Rozwiązanie to jest niefizyczne i powinniśmy je “zmodyfikować” tak, by było ono fizyczne (funkcja f MUSI dla dostatecznie dużych
zmierzać do zera).

Jeden sposób (czy potraficie znaleźć inny?) polega na wykorzystaniu postaci wzoru rekurencyjnego (34). Zauważmy bowiem, że gdyby
było równe
, gdzie n jest dowolną liczbą całkowitą większą od 0, to
, a także następne współczynniki rozwinięcia potęgowego funkcji g, będą równe 0. W ten sposób funkcja g wyrazi się skończonym, a nie nieskończonym wielomianem, który będzie rósł z
wolniej niż funkcja eksponencjalna, a funkcja f będzie zmierzała do zera dla
zmierzającego do nieskończoności. Przy takim warunku narzuconym na
mamy
, czyli:

. (35)

Dopuszczone są zatem nie wszystkie, lecz tylko dyskretne wartości energii, dokładnie tak jak w teorii Bohra. Podobnie jak w teorii Bohra, n będzie zatem główną liczbą kwantową. Część radialna funkcji falowej, dla
, wyrazi się w następujący sposób:

(36)

gdzie: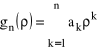
(37)

oraz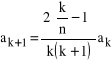
(38)

a wartość pierwszego ze współczynników
można na razie przyjąć jako równą 1 zostawiając sprawę unormowania całkowitej funkcji falowej na później. Jak widać ze wzorów, wypisanie postaci radialnej funkcji falowej dla dowolnego n, dla
(czyli funkcji falowej, czy też stanu ns), to sprawa rzeczywiście bardzo prosta; dla przykładu:

dla n = 1, mamy

dla n = 2, mamy

dla n = 3, mamy
itd.

Rozwiązania równania radialnego z zależnością kątową
.

Wracamy do równania (25), ale tym razem nie pomijamy wyrazu z orbitalnym momentem pędu L:

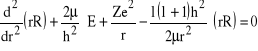
(39)

gdzie, zgodnie z (20),
jest wartością własną operatora kwadratu całkowitego momentu pędu
, lub też, mówiąc prościej,
jest wartością momentu pędu L. Zatem dodatkowy wyraz w równaniu (39) ma postać
, i przedstawia energię kinetyczną związaną z ruchem obrotowym, podobnie jak wyrażenie
przedstawia energię kinetyczną w ruchu postępowym (w ruchu obrotowym moment pędu gra rolę pędu w ruchu postępowym, a moment bezwładności
gra rolę masy). Dodanie tego wyrazu do równania (39), po wykonaniu, analogicznie jak dla przypadku sferycznego, podstawień,
, gdzie
to promień Bohra, oraz
, gdzie
to stała Rydberga (13,6 eV), otrzymamy:

, (40)

(porównajcie to równanie z równaniem (26)). Widać, że możemy postępować analogicznie jak w przypadku kulistosymetrycznym, uwzględniając dodatkowy wyraz w rozwinięciu funkcji g, który będzie miał postać: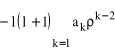
(-2 w wykładniku bierze się z dzielenia przez
). Wydzielając pierwszy wyraz i przenumerowując całą sumę otrzymamy: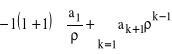
, co odpowiednio zmodyfikuje wyrażenie (31) i (32), dając:

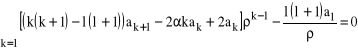
. (41)

Warunek zerowania oznacza, iż
musi być równe zero (nie może być inaczej, gdyż
), a także, z warunku zerowania współczynników przy kolejnych wyrazach mamy:

(42)

skąd otrzymujemy zmodyfikowany związek rekurencyjny na współczynniki rozwinięcia potęgowego funkcji g:

(43)

Podobnie jak poprzednio szereg musi się urywać, co zajdzie dla k = n, gdy
; zeru będzie równy wyraz
. Ponieważ
, także kolejne wyrazy będą równe 0, aż do
, dla którego współczynniki przy obu wyrazach a_k i a_k+1 są równe 0. Oznacza to, że wyraz a_l.+1 (dla
) jest pierwszym wyrazem, który może być różny od zera, no i oczywiście różne do zera będą kolejne wyrazy, aż do wyrazu dla którego
(to będzie ostatni różny od zera wyraz sumy przedstawiającej funkcję g). Ostatecznie dopuszczalne rozwiązania na funkcję g są takie, dla których k zaczyna się od
i kończy na n. Oznacza to oczywiście, że dla danego n (pamiętamy, że n to jest główna liczba kwantowa), dozwolone wartości
biegną od 0 do
. Dla
równych lub większych od n, funkcji g, czyli także całej funkcji radialnej, po prostu nie ma. Liczbę
nazywamy liczbą kwantową orbitalnego momentu pędu, lub poboczną liczbą kwantową.

Warto zauważyć, że dla małych
w funkcji R, równej
, dominować będzie wyraz z
. Oznacza to, że funkcje odpowiadające większej wartości
będą się wyraźnie różnić od zera dalej od jądra (większe
).

Kilka pierwszych funkcji R(r), dla różnych wartości głównej i pobocznej liczby kwantowej, podajemy poniżej:

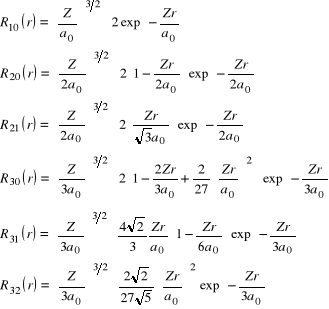
(43)

Podsumowując, następujące liczby kwantowe: n - główna liczba kwantowa,
- poboczna liczba kwantowa lub liczba kwantowa orbitalnego momentu pędu, m - magnetyczna liczba kwantowa, określają stan atomu wodoru (jonu wodoropodobnego) i jego energię (degeneracja ze względu na
i m). Funkcje falowe dla
i różnych wartości n, zawierają tylko część radialną i mają symetrię sferyczną (funkcje, lub stany s), natomiast funkcje falowe dla
, zawierają oprócz części radialnej, także część kątową (funkcje kuliste, wzory (16)). Będą to funkcje p (dla
), d (dla
), f (dla
), g (dla
) itd. Pochodzenie liter s, p, d, f ma źródło historyczne, dalej zaś stosujemy kolejność alfabetyczną.

Schemat poziomów energetycznych atomu wodoru, z uwzględnieniem liczby n i
.

Rysunek: Schemat poziomów energetycznych atomu wodoru (proporcje nie są zachowane), nazywany często diagramem termów Grotriana. Dla jonów wodoropodobnych skala energii musi być odpowiednio zmieniona ze względu na Z. Poziomy dla tego samego n ale różnych
mają taką samą energię (degeneracja orbitalna).

6b. Atomy wieloelektronowe, układ okresowy, sposób wypełniania elektronami stanów elektronowych w atomach wieloelektronowych
(zalecany podręcznik, Feynmana wykłady z fizyki, III tom, rozdz. 19, podrozdz. 19-6)

Zasada Pauliego (więcej na ten temat w następnych wykładach), przybliżenie pola centralnego (jednoelektronowe).

1s
2s, 2p
3s, 3p, 3d
4s, 4p, 4d, 4f
5s, 5p, 5d, 5f, 5g
6s, 6p, itd.

ze względu na usunięcie degeneracji ze względu na liczbę kwantową momentu pędu
kolejność zapełniania powłok jest czasem zmieniona (ekranowanie, stany o niższej liczbie kwantowej
i wyższej liczbie n mogą leżeć niżej energetycznie i być wcześniej zapełnione), patrz przykład niżej dla metali alkalicznych.

Atomy wieloelektronowe

Punktem wyjścia schemat poziomów jednoelektronowych dla atomu wodoru. Są jednak konieczne modyfikacje, większe dla bardziej zewnętrznych elektronów, wywołane ekranowaniem ładunku jądra przez elektrony o niższej głównej liczbie kwantowej n (zależność przestrzennej funkcji falowej od Z; zmiany średniego rozkładu ładunku). Te modyfikacje (metoda Hartree'ego), stanowią częściowe uwzględnienie oddziaływania pomiędzy elektronami (nieuwzględniona część to głównie tzw. oddziaływanie niecentralne). Jakościowy opis metody Hartree'ego, wyjściowe funkcje falowe, rozkład ładunku pozostałych elektronów, potencjał całkowity widziany przez dany elektron, numeryczne rozwiązanie równania Schrődingera i nowa funkcja falowa dla danego elektronu, powtarza się tę procedurę dla wszystkich elektronów, mając nowe funkcje powtarza się cała procedurę aż do osiągnięcia "samouzgodnienia", czyli gdy zmiany energii i funkcji falowych dla wszystkich elektronów są nieznaczne. Wynik końcowy, energie jonizacji różnych atomów, stabilność wypełnionych powłok, elektrony walencyjne, własności chemiczne: jonowość i wiązania jonowe. Zniesienie degeneracji ze względu na azymutalną liczbę kwantową (poboczną, lub liczbę kwantową momentu pędu, zmiana kolejności obsadzanych poziomów jednoelektronowych, przypadek elektronów 3d i 4f (atomy metali przejściowych i ziem rzadkich). Układ okresowy pierwiastków, własności chemiczne i ich okresowość, energie jonizacji dla kolejnych atomów, trendy, osobliwości i ich wytłumaczenie (Feynman).

6c. Widma atomów metali alkalicznych; usunięcie degeneracji orbitalnej
(zalecany podręcznik: H. Haken, H.C. Wolf, Atomy i kwanty)

Metale alkaliczne, jeden zewnętrzny elektron walencyjny

Li
, w stanie podstawowym konfiguracja: 1s²2s [He]2s

Na
, w stanie podstawowym konfiguracja: 1s²2s²2p⁶3s [Ne]3s

K
, w stanie podstawowym konfiguracja: 1s²2s²2p⁶3s²3p⁶4s [Ar]4s

Rb
, w stanie podstawowym konfiguracja: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s [Kr]5s

Cs
, w stanie podstawowym konfiguracja: 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s [Xe]6s

Model atomu metalu alkalicznego, ekranowanie, potencjał efektywny

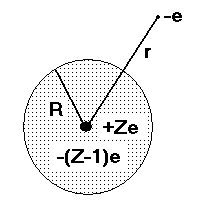
Rys. Model atomu metalu alkalicznego. Jądro o ładunku +Ze jest otoczone elektronami z wewnętrznych zapełnionych powłok o łącznym ładunku -(Z-1)e, skupionymi w obszarze o promieniu R.

W modelu przedstawionym na rysunku pojedynczy zewnętrzny elektron walencyjny przebywa głównie (choć nie wyłącznie) w obszarze gdzie r > R. Efektywny potencjał, “widziany” przez elektron, zależy od położenia elektronu r i może przyjmować wartości pomiędzy -e²/r (dla r > R) i -Ze²/r (dla elektronu bardzo blisko jądra, r <<R).

Ponieważ, jak wynika z naszej wcześniejszej analizy funkcji radialnych, dla rosnącej liczby kwantowej orbitalnego momentu pędu
(dla tego samego n) prawdopodobieństwo przebywania elektronu w pobliżu jądra maleje, elektrony w tych stanach “widzą” silniej ekranowany potencjał i odpowiadające im poziomy energetyczne (termy) leżą bliżej odpowiednich termów dla atomu wodoru i degeneracja orbitalna zostaje zniesiona (patrz rys. niżej)

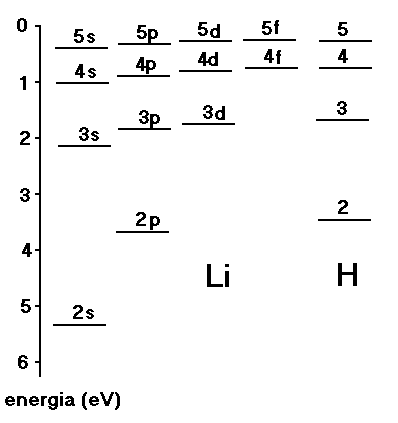
Rys. Diagram Grotriana (układ termów) atomu litu Li i, dla porównania, wodoru H.

Termy energetyczne dla atomu metalu alkalicznego określone przez liczby kwantowe n i
można wyrazić w następujący sposób:

(32)

gdzie
jest efektywną główną liczbą kwantową “poprawioną” o wartość
, zwaną defektem kwantowym zależną od obu liczb kwantowych, głównej liczby n i liczby kwantowej orbitalnego momentu pędu
(bardzo słabo od n i stosunkowo silnie od
). Silna zależność defektu kwantowego od liczby
wynika z różnego stopnia ekranowania potencjału jądra przez elektrony wewnętrznych powłok dla elektronu zewnętrznego znajdującego się w stanach o różnych wartościach
.

Żeby znaleźć liczby falowe (lub energie) odpowiadające różnym dozwolonym seriom przejść w atomach metali alkalicznych, należy wykorzystać wzór (32) biorąc pod uwagę, że dozwolonym przejściom odpowiada
. Będzie to wyglądało następująco:

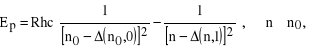
seria główna (principal) (3s - np), w tym linia D (3s - 3p).

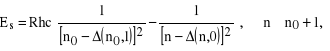
seria ostra (sharp), inaczej II poboczna (3p - ns)

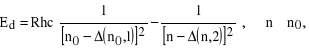
seria rozmyta (diffuse), inaczej I poboczna (3p - nd)

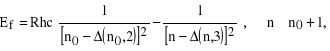
seria podstawowa (fundamental), albo Bergmanna (3d - nf).

We wzorach tych
jest główną liczbą kwantową (całkowitą), najniższego stanu dla elektronu walencyjnego: dla Li
, dla Na
jak w przykładzie wyżej, dla K
, dla Rb
i dla Cs
, natomiast
jest defektem kwantowym.

Tylko w bardzo wysokich temperaturach obserwować można linie absorpcyjne dla serii innych niż główna, zatem tylko linie serii głównej są liniami rezonansowymi w warunkach normalnych.

Dla przykładu wartości defektu kwantowego dla różnych stanów atomu Na podano w tabeli poniżej.

TABELA. Wartości defektu kwantowego wyznaczone doświadczalnie z widma atomu Na (F. Richtmyer, E. Kennard, J. Cooper, Introduction to Modern Physics, wyd. 6, McGraw-Hill, New York 1969).

	stan	n = 3	4	5	6	7	8
1 2 3	s p d f	1.373 0.883 0.010 -	1.357 0.867 0.011 0.000	1.352 0.862 0.013 -0.001	1.349 0.859 0.011 -0.008	1.348 0.858 0.009 -0.012	1.351 0.857 0.013 -0.015

ZADANIA do wykładu 7,8 i 9 (wybór z podręcznika Haken, Wolf, Atomy i kwanty)

1. Zmierzone wartości defektu kwantowego
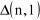
   dla litu i sodu wynoszą:

	s	p	d
Li (Z = 3) Na (Z = 11)	0.40 1.37	0.04 0.88	0.00 0.01

Oblicz energię stanu podstawowego i dwóch pierwszych stanów wzbudzonych elektronu walencyjnego w atomach Li i Na.

2. Energia jonizacji atomu Li wynosi 5,3913 eV, a linia rezonansowa (2s ↔ 2p) obserwowana jest przy 6710 Å. Wzbudzenie litu w fazie gazowej prowadzone jest selektywnie , tak że obsadzony jest tylko poziom 3p. Jakie linie widmowe emitowane są przez ten gaz i jaka jest ich długość? (Wskazówka: Skorzystaj z założenia, że defekt kwantowy nie zależy od głównej liczby kwantowej n).

Wykład 8 9 i 10, strona 1

---