3.Linia jednostronnie i dwustronnie zasilana

Strata napięcia - geometryczna różnica wektorów napięć w dwóch punktach zasilania sieci.

Spadek napięcia - różnica modułów (wartości skutecznych) napięć istniejących w dwóch punktach sieci.

Dla prądu przemiennego stratę napięcia dzielimy na:

1. czynną - wywołaną spadkiem napięcia na rezystancji;

2. bierną - spowodowaną spadkiem napięcia na reaktancji.

W przypadku prądu stałego - występuje tylko strata czynna napięcia (równa spadkowi napięcia).

3.1.Linia jednostronnie zasilana

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)

Maksymalny spadek ΔU_om pomiędzy punktami „O” i „m” wyznaczyć można metodą:

1. odcinkową;

2. momentów względem najdalszego punktu odbioru lub względem punktu zasilania.

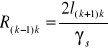
3.1.1.Metoda odcinkowa

Równanie ogólne odcinka

(3.6)

Przy założeniu, że przewody są tego samego materiału (tj. γ i s = const na całej długości) równanie (3.6) przyjmuje postać

(3.7)

3.1.2.Metoda momentów względem punktu zasilania

Równanie ogólne spadku napięcia

(3.8)

z którego wynika, że spadek napięcia można określić sumując „momenty prądowe” odpowiedniemu iloczynowi pradu I_k i rezystancji R_ok przewodu odcinka linii od punktu zasilania do miejsca jego odpływu.

Gdy γ i s = const równanie (3.8) przyjmuje postać

(3.9)

gdzie

I_ok - długość odcinka linii od punktu „o” do punktu „k”.

3.2.Linia jednostronnie zasilana prądu przemiennego I i II rodzaju

W liniach prądu przemiennego należy uwzględnić rezystancje i reaktancje, przesunięcia fazowe prądów względem napięcia, obciążenia czynne i bierne, straty i spadki napięć.

Na rysunku 3.2a jednostronnie zasilaną trójfazową linię symetryczną posiadającą jednakową rezystancję (R_o1), reaktancje (X_o1), prąd odcinkowy (I₀₁) w każdej fazie.

Strata napięcia:

(3.10)

Spadek napięcia:

(3.11)

Na rysunku 3.2b oznaczono: czynną tratę napięcia - ΔU_R, bierną stratę napięcia - ΔU_X, podłużną stratę napięcia - ΔU^'₀₁, poprzeczną stratę napięcia - ΔU^”₀₁.

W linii drugiego rodzaju kąt β ≈ 0, stąd odcinek AD odpowiada spadkowi napięcia (wyrażona poprzez podłużną stratę napięcia)

(3.12)

Ogólne wzory na podłużną i porzeczną stratę napięcia posiadają postać

(3.13)

(3.14)

w których

1. przy obciążeniu indukcyjnym prądy bierne I wstawiamy ze znakiem „-”;

2. przy obciążeniu pojemnościowym ze znakiem „+”.

(3.15)

(3.16)

(3.17)

(3.18)

(3.19)

(3.20)

(3.21)

Rys.3.3. Możliwe wartości napięcia Δ₀₁ przy stałej wartości straty napięcia ( w zależności od rodzaju impedancji) ΔU₀₁:

1. spadek napięcia dodatni 9obwód indukcyjny);

2. spadek napięcia ujemny ( w obwodzie pojemnościowym - występuje wzrost napięcia).

3.3.Obliczenie rozpływu prądów w liniach I i II rodzaju posiadających m obwodów

Równanie prądów odcinkowych

(3.22)

(3.23)

(3.24)

(3.25)

gdzie I^'_k, I^”_k - prąd czynny i bierny k-tego odbioru.

3.4.Obliczenie spadków napięć w liniach I i II rodzaju posiadających m odbiorów

Obliczenia prowadzi się metodą odcinkową lub momentów (tak samo jak prąd stały).

Stosując metodę odcinkową dla linii II rodzaju, ogólny wzór na spadek napięcia ma postać

(3.26)

W liniach I rodzaju (w których X = 0) wzór na spadek napięcia upraszcza się do odpowiedniej postaci:

(3.27)

(3.28)

Gdy γ i s = const oraz trójfazowa linia jest symetryczna, wzory (3.27) i (3.28) przyjmują postać:

(3.29)

(3.30)

3.5.Sprowadzenie linii do wspólnego przekroju

Jako przekrój zastępczy przyjmuje się przekrój dominujący w linii lub inny zastępczy. Wzór na długość zastępczą przewodu I_z(k-1)k wyznaczamy ze wzoru:

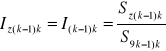
(3.31)

gdzie

I_(k-1)k - długość przewodu o przekroju pierwotnym S_(k-1)k

S_z(k-1)k - przekrój zastępczy przewodu

3.6.Linia jednostronnie zasilana obciążona równomiernie

Założenie: linia trójfazowa symetryczna I rodzaju obciążona na całej długości I_om obciążeniem jednostronnym τ. Elementarny spadek napięcia

(3.32)

Po scałkowaniu na całej długości I_om

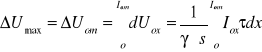
(3.33)

Wyrażając całkowite obciążenie linii wzorem

(3.34)

Całkowity spadek napięcia linii obciążonej równomiernie wynosi

(3.35)

3.7.Linia dwustronnie zasilana prądem przemiennym I i II rodzaju

3.7.1.Rozpływ prądu

(3.36)

Jak ta suma pradu rozłoży się na każdej z punktów zasilających? Podstawą obliczeń jest przyjęte, ze strata napięcia wzdłuż linii (tj. od punktu 0 do punktu m) jest równa sumie strat napięć w poszczególnych jej odcinkach

(3.37)

W wzorze (3.37) zakłada się, że znana jest strata napięcia ΔU_om i impedancje odcinkową Z_(k-1) oraz ΔU₀ ≥ ΔU_m.

W celu obliczonego nieznacznego prądu odcinka wyraża się go znanymi prądami odbiorców oraz nieznanym prądem zasilającym, np. I₀.

Straty napięcia w poszczególnych odcinkach można zapisać równaniem:

(3.38)

zapisanym w postaci ogólnej (takiej samej jak w metodzie momentów prądów względem punktu m).

(3.39)

Z (3.38) wyznaczyć można prąd zasilający I₀ = I₀₁

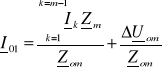
(3.40)

Podstawą analizy wyznaczyć można prąd zasilający I_m, (wyznaczyć dla momentu prądów względem punktu o) opisany równaniem

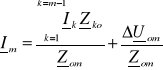
(3.41)

Pierwszy człon wyżej wymienionych równań przedstawia prądy składowe (tj. prądy płynące w linii dwustronnie zasilanej przy jednakowym napięciu w punktach zasilania)

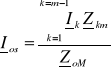
(3.42)

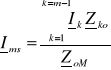
Drugi człon, jednakowy w obydwu przypadkach, prąd wyrównawczy płynąc wzdłuż całej linii wskutek istnienia różnicy geometrycznej napięć zasilających

(3.43)

Jeżeli prądy zasilające są równe, to wówczas w linii nie płynie prąd wyrównawczy, a tylko prądy składowe.

Jeżeli prądy odbiornika są równe zeru, a napięcie zasilania nie są równe zero, wtedy w linii płynie tylko prąd wyrównawczy.

Rozpływ prądów w poszczególnych odcinkach uzyskuje się przez nałożenie prądów składowych i prądu wyrównawczego. O kierunkach prądu odcinkowego decyduje jego część rzeczywista. W wyniku nałożenia prądów może wystąpić w linii punkt o najniższym potencjale, zwany punktem spływu prądów. Gdy nie ma ww. punktu spływu, to wówczas jedno ze źródeł zasila drugie. (Rys.3.6.)

3.7.2.Spadek napięcia

Spadek napięcia do punktu spływu (rys.3.6) można obliczyć albo od punktu 0 albo od punktu 3 (np. metodą odcinkową). Dla linii II rodzaju spadek napięcia można zapisać równaniem

(3.44)

Dla linii I rodzaju wzór (3.44) upraszcza się do postaci

(3.45)

Dla prądu stałego stosujemy wzór (3.45) z tą różnicą, że prąd I^'_(k-1)k zastępujemy prądem stałym.

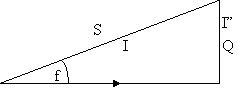
3.7.3.Spadek napięcia w linii przesyłowej III rodzaju

Schemat linii III rodzaju - czwórnik typu π - rys.3.7.

W celu wyznaczenia straty i spadku napięcia prądu zasilającego, współczynnika mocy, napięcie na początku linii przesyłanej założono, że dane są:

1. U₁₂ - napięcie fazowe na końcu linii;

2. I₂ - prąd odbioru ma końcu linii;

3. cosφ₂ - współczynnik mocy na końcu linii obciążenie ma charakter indukcyjny, tzn. φ₂ <.

Wykres wektorowy napięć i prądów linii przesyłowej III rodzaju. Moduły wyznacza się z:

(3.46)

Fazowy spadek napięć (równy odcinkowi AE otrzymany przez zatoczenie z punktu 0 łuku o promieniu OB.) określa wzór

(3.47)

natomiast fazową stratę napięć wyznacza się ze wzoru:

(3.48)

zawiera wzdłużną (odcinek AD) i poprzeczną (odcinek DB).

Zatem w liniach III rodzaju:

1. poprzeczna starta napięcia ma istotny wpływ na ΔU, stąd musi być uwzględniona (w przeciwieństwie do linii I i II rodzaju, gdzie była zaniedbywana i nieuwzględniania),

2. spadek napięcia jest różny od podłużnej straty napięcia ( o odcinku DE).

3.7.4.Sieci wielokrotnie zamknięte

Obliczenia rozpływów prądów i spadek napięć przeprowadza się metodą sieci węzłowych - wyznaczając potencjały węzłowe przy znanych węzłach adamitancyjnych własnych i wzajemnych. Otrzymane zależności zapisuje się równaniami macierzowymi i rozwiązuje metodami iteracyjnymi - tj. kolejnych przybliżeń.

Obliczenie spadku napięcia w prostych układach sieciowych.

(3.49)

(3.50)

(3.51)

(3.52)

- przekładnia transformatora

11 - liczba transformacji

9

---