Statystyka zajmuje się ilościowymi metodami badania zjawisk masowych, tj. takich, w których występuje duża liczba jednostek.
Przedmiotem badania jest:
Populacja (zbiorowość statystyczna), tj. zbiór elementów podobnych (jednostek statystycznych), odznaczających się pewnymi właściwościami (cechami).
Najczęściej jednak badającemu dostępna jest:
Próba (zbiorowość próbna), tj. podzbiór populacji obejmujący wybrane w określony sposób elementy (losowy, celowy). Własności tego podzbioru są badane w uogólniane na całą populację.
Badania statystyczne można podzielić na:
całkowite (pełne), gdy obejmuje wszystkie elementy populacji, np. spis powszechny, sprawozdawczość finansowa
częściowe (niepełne), gdy dostępna badaczowi jest jedynie próba np. badania analityczne, monograficzne, reprezentacyjne
Etapy badania statystycznego:
przygotowanie badania (ustalenie celu i metody badania)
obserwacja statystyczna (ustalenie wartości cech jednostek)
opracowanie materiału statystycznego (grupowanie i zliczanie)
prezentacja materiału (tablice i wykresy)
wnioskowanie statystyczne (uogólnianie wyników badań próby na całą zbiorowość statystyczną) lub opis elementów w próbie za pomocą miar statystycznych
Rodzaje cech (reprezentowanych przez zmienne)
jakościowe (niemierzalne) np. płeć, wykształcenie, zawód
ilościowe (mierzalne) np. płaca, wartość produkcji
skokowe - przyjmują wartości ze skończonego zbioru wartości np. liczba studentów w grupie, liczba dzieci itp.
ciągłe - przyjmują wartości z nieprzeliczalnego zbioru wartości wynika to z dokładania pomiaru np. wzrost, waga, wartość spadku
Szeregi statystyczne
szczegółowe (wyliczające): x1, x2, x3, ..., xn
rozdzielcze:
miary pieniężne (średnie) charakteryzują średnią wartość cechy dla jednostek w próbie
zróżnicowanie (zmniejszenie) charakteryzująca stopień zróżnicowania jednostki w próbie
miara asymetrii (skośność) pokazuje czy więcej jednostek ma wartość cechy większą lub mniejszą od średniej
dla szeregu szczegółowego:
dla szeregu rozdzielczego cechy skokowej (o „k” wartościach)
dla szeregu rozdzielczego cechy ciągłej (dla „k” przedziałów)
szereg szczegółowy - wartość występująca najczęściej
szereg rozdzielczy dla cechy skokowej - wartość o największej liczebności:
kwartyle - podział na 4 częścidecyle - podział na 10 części
centyle - podział na 100 części
szereg szczegółowy - należy uporządkować rosnąco i obliczyć:
szereg rozdzielczy dla cechy skokowej - należy skumulować liczebności (lub częstości względne) i znaleźć wartości dla której częstość ≥ 50%
szereg rozdzielczy dla cechy ciągłej - skumulować liczebności i znaleźć przedział, w którym częstość względna ≥ 50% oraz wykorzystać wzór:
klasyczne
pozycyjne
dla szeregu szczegółowego
dla szeregu szczegółowego:
dla szeregu rozdzielczego
Rozstęp (obszar zmienności)
Odchylenie ćwiartkowe
Wskaźnik asymetrii (mówi o kierunku asymetrii)
klasyczny
pozycyjny
Współczynnik asymetrii (mówi o kierunku i o sile asymetrii)
klasyczny
pozycyjny
Współczynnik korelacji liniowej Pearsona:
„Y” względem „X” (wpływ „X” na „Y”)
gdzie metodą najmniejszych kwadratów (MNK) można wyznaczyć wartości parametrów „a” i „b”
„X” względem „Y” (wpływ „Y” na „X”)
która ocenia rozproszenie wartości empirycznych wokół teoretycznych.
przyjmuje wartości z przedziału [0, 100%]. Ocenia: w jakiej części zmiany cechy „y” nie są wyjaśnione zmianami cechy „x”. Im bliżej „0”, tym lepsza funkcyjna regresja (modelu).przyjmuje wartości z przedziału [0, 100%]. Informuje o tym, jaka część zmian cechy „y” jest wyjaśniona przez funkcję regresji. Im bliżej 100%, tym lepsza model.
2 rozkłady brzegowe (rozkład cechy X oraz rozkład cechy Y)
„s + t” rozkładów warunkowych
cecha „X”
cecha „Y”
cecha „X” (tyle rozkładów, ile wartości cechy „Y”)
cecha „Y” (tyle rozkładów, ile wartości cechy „X”)
„X” jest niezależne stochastycznie od „Y” jeśli:
„Y” jest niezależne stochastycznie od „Y” jeśli:
„X” jest niezależne korelacyjnie od „Y” jeśli:
„Y” jest niezależne korelacyjnie od „Y” jeśli:
jeśli wraz ze wzrostem (spadkiem) wartości jednej cechy rosną (spadają) średnie warunkowej drugiej, to związek jest dodatni
jeśli wraz ze wzrostem (spadkiem) wartości jednej cechy spadają (rosną) średnie warunkowej drugiej, to związek jest ujemny
„X” względem „Y”
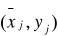
„Y” względem „X”
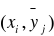
Cechy nominalne
taka sama jak tablica korelacyjna
cecha y - nazwy i cecha x - nazwy, wewnątrz tablicy liczebności
współczynnik Czuprowa
współczynnik Cramera
im bliżej „1” - tym silniejsza zależność cech „X” i „Y”
Cechy porządkowe (np. ocena, wykształcenie)
współczynnik korelacji rang Spearmana
informuje ona o sile i kierunku związku, gdzie:
to szereg szczegółowy, uporządkowany ze względu na czas, który reprezentują kolejne numery: 1,…, n
ogólny wzór:
interpretacja:
o podstawie stałej (jednopodstawowe) okresem bazowym jest y1:
pokazują zmiany w kolejnych okresach (momentach) w porównaniu z okresem (momentem) podstawowym (jest ich „n”, tj. tyle, ile elementów szeregu czasowego)
łańcuchowe
pokazują zmiany w kolejnych okresach (momentach) czasu w porównaniu z okresem (momentem) poprzednim (jest ich „n-1”, tj. brak jest pierwszego)
to średnia geometryczna z indeksów łańcuchowych, którą w skrócie można zapisać jako:
określa poszczególne zmiany wartości cechy z okresu (momentu) na okres (moment):
pozwalają analizować zmiany cen (p), ilość (q) i wartość (qp) pojedynczych produktów (wyrobów)
cen
ilości
wartości
pozwalają analizować zmiany wartości cen oraz ilości zbioru grupy) produktów (wyrobów, artykułów), które nie są jednorodne, np.: „nabiał” oznacza zarówno mleko, sery, jak i jajka, mierzone w zupełnie inny sposób
wartości
ilości Laspeyresa
ilości Paaschego
cen Laspeyresa
ilości Fishera
cen Fishera
gdy efekt działania czynników sezonowych jest proporcjonalny do funkcji trendu (model multiplikatywny)
gdy efekt działania czynników sezonowych jest stały w poszczególnych okresach (model addytywny)
- dla cechy skokowej |
|
- dla cechy ciągłej |
||
Wartość cechy |
Liczebność |
|
Wartość cechy |
Liczebność |
x1 |
n1 |
|
x1- x2 |
n1 |
x2 |
n2 |
|
x2 - x3 |
n2 |
... |
... |
|
... |
... |
xk |
nk |
|
xk - xk + 1 |
nk |
razem |
|
|
razem |
|
Miary służące do opisu cech jednostek statystycznych należących do próby:
Średnia arytmetyczna
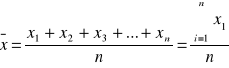
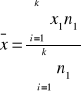
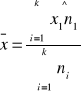
Średnia harmoniczna:
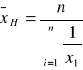
Średnia geometryczna:
![]()
Dominanta (moda) to wartość cechy, która występuje najczęściej, jest typowa:
![]()
gdzie:
xD - dolna granica
nD - liczba przedziału
nD-1 - liczba przedziału poprzedniego
nD+1 - liczba przedziału następnego
iD - szerokość przedziału dominanty
Przykład 1.
Xi |
Ni |
Xi |
Xi * Ni |
Wi |
Wisk |
0-1000 1000-2000 2000-3000 3000-4000 4000-5000 |
8 18 12 8 4 |
500 1500 2500 3500 4500 |
4000 27000 30000 28000 18000 |
16% 36% 24% 16% 8% |
16% 52% 76% 92% 100% |
Ogółem: |
50 |
- |
107000 |
100% |
- |
Typowa wielkość oszczędności to 1625zł.
Kwantyle - dzielą uporządkowany rosnąco (lub malejąco) wg wartości określonej cechy zbiór jednostek na odpowiednią liczbę części:
Q1 (kwartyl pierwszy) - dzieli jednostki na 2 części: 25% z nich ma wartości cechy mniejsze od niego, zaś 75% - większe
Me (mediana) - dzieli jednostki na dwie równe części
Q3 (kwartyl trzeci) - dzieli jednostki na 2 części: 75% z nich ma wartości cechy mniejsze od niego, zaś 25% - większe
Mediana
![]()
, gdy n jest parzyste
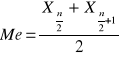
, gdy n jest nieparzyste
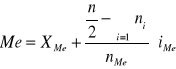
gdzie:
XMe - dolna granica przedziału mediany
nMe - liczebność przedziału mediany
iMe - szerokość przedziału mediany
n - liczebność próby
Ad. Przykład 1.
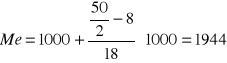
Połowa osób ma na koncie mniej niż 1944zł, a połowa powyżej.
Kwartyl I 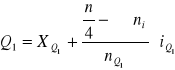
Kwartyl III 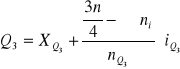
Miary statystyczne
Wymagają one znajomości wszystkich wartości cechy, tj. aby wszystkie przedziały były domknięte. Są obiektywne, ale bardzo wrażliwe na błędy oraz tzw. wartości oddalone
Np. średnia arytmetyczna
Nie wymagają znajomości wszystkich wartości cechy, tj. niektóre przedziały mogą być otwarte. Ich wartość wynika z położenia w szeregu, co oznacza, że są subiektywne. Nie są jednak wrażliwe na błędy, wartości oddalone
Np. mediana
Koncepcja sposobu oceny stopnia zróżnicowania
Miary zróżnicowania
Wariancja
![]()
![]()
gdzie m2 i m1 to tzw. drugi i pierwszy moment zwykły
Moment zwykły rzędu „k” to:
![]()
![]()
Miary Pozycyjne Zróżnicowania
![]()
![]()
Miary Pozycyjne Względne
1) Współczynnik zmienności
![]()
![]()
Miary Asymetrii (Skośności)
![]()
![]()
WS > 0 - asymetria prawostronna
WS = 0 - symetria
WS < 0 - asymetria lewostronna
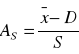
lub
![]()
AS > 0 - asymetria prawostronna
AS = 0 - symetria
AS < 0 - asymetria lewostronna
S - odchylenie standardowe
M3 - trzeci moment centralny (wariancja drugi moment)
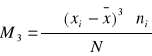
![]()
Wykresy:
Dane są źle zebrane - nie powinno się nic dalej robić
AS <-1,1> silna asymetria albo lewo- albo prawostronna (jeżeli bliżej -1 lub 1)
AS <-0,3;0,3> umiarkowana asymetria
(powyżej 0,3 lub poniżej -03 asymetria dosyć wyraźna
Koncentracja kurtoza (w Excelu)
Korelacja i regresja
gdzie:
cor(x,y) to kowariacja - miara wspózmienności
przyjmująca wartości z: przedziału: [-s(x)s(y), +s(x)s(y)].
Współczynnik korelacji mówi nam o kierunku i sile między zmiennymi.
Przyjmuje wartości: r ∈ [-1, 1]
Wartość współczynnika mówi o sile związku. Im jest bliższa zera - tym słabszy związek, im bliżej 1 lub -1 tym silniejszy. Wartość |1| oznacza idealny związek liniowy.
Znak współczynnika korelacji mówi o kierunku związku:
„+” - oznacza związek dodatni, tj. wzrost (spadek) wartości jednej cechy powoduje wzrost (spadek) wartości drugiej
„-” - oznacza ujemny kierunek, tj. wzrost (spadek) wartości jednej cechy powoduje spadek (wzrost) wartości drugiej.
do 0,3 - słaba
od 0,3 do 0,5 - średnia
powyżej 0,5 - wyraźna
Wykres rozrzutu (diagram korelacyjny) wykres x,y (w Excelu)
Jakich związków „r” nie wykryje?
- nieliniowych
Linia (Model) Regresji (II Rodzaju)
![]()
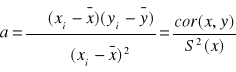
bezpośrednia
![]()
Parametr „a” można także obliczyć korzystając z wzoru:
![]()
pośrednia
Interpretacja parametru „a”:
a > 0 - wzrost „x” o 1 jednostkę powoduje wzrost „y” średnio o „a” jednostek
a < 0 - wzrost „x” o 1 jednostkę powoduje spadek „y” średnio o „a” jednostek
„a” i „r” zawsze mają te same znaki
![]()
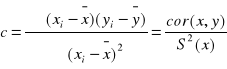
![]()
![]()
Pomiędzy współczynnikami prostych regresji „a” i „c” zachodzi związek:
![]()
Dokładność Funkcji Regresji
Ocena dopasowania modelu do danych empirycznych: jej pomiar opiera się na obliczeniu „reszt”, tj. różnic
![]()
gdzie:
![]()
- wartość empiryczna cechy „y”
![]()
wartość
Renta określa niedokładność szacunku i-tej wartości cechy.
Syntetycznym miernikiem jakości modelu jest tzw. wariacja resztkowa
S(u) to odchylenie standardowe reszt, które mówi o tym, jakie jest przeciętne odchylenie wartości empirycznych od wartości teoretycznych. Im bliższe zeru, tym lepsza funkcja regresji (modelu)
Współczynnik zbieżności
Współczynnik determinacji
Tablica Korelacyjna
|
Cecha Y |
||||
Cecha X |
|
Y1 |
... |
Yt |
|
|
X1 |
N11 |
... |
N1t |
N1k |
|
X2 |
N21 |
... |
N2t |
N2k |
|
... |
... |
... |
... |
... |
|
Xs |
Ns1 |
... |
Nst |
Nsk |
|
|
Nk1 |
... |
Nkt |
N |
W kolumnach znajdują się wartości (lub przedziały wartości) cechy Y, a w wierszach wartości (lub przedziały wartości) cechy X. Wewnątrz tablicy są liczebności. Przy czym:
![]()
Tablica korelacyjna opisuje:
Charakterystyka rozkładów brzegowych:
![]()
![]()
![]()
![]()
Charakterystyka rozkładów warunkowych:
Rozkład warunkowy opisuje zachowanie jednej cechy, pod warunkiem, że druga cecha przyjęła określoną wartość (X/Y = yj lub Y/X = xi)
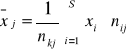
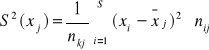
![]()
![]()
Współczynnik korelacji liniowej Pearsona (miara symetryczna)
![]()
gdzie:
![]()
Współczynnik korelacji liniowej Pearsona (miara niesymetryczna)
Charakter siły związku zarówno liniowego, jak i nieliniowego (nie kierunek) przyjmuje wartości z przedziału <0,1>
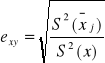
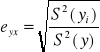
Im wartość bliższa „1”, tym związek korelacyjny jest silniejszy. Wartość „1” oznacza związek, przy czym:
![]()
![]()
,
to tzw. relacje międzygrupowe.
Wskaźniki krzywoliniowości
Oceniają „stopień” nieliniowości związku między X i Y. Przyjmują wartości z przedziału <0,1>.
![]()
![]()
m ≤ 0,2 to związek można uznać za liniowy
m > 0,2 to związek można uznać za liniowy
Niezależność stochastyczna
![]()
![]()
![]()
![]()
Niezależność korelacyjna
![]()
![]()
Ocena kierunku związku
Regresja I rodzaju
Jest to przyporządkowanie wartościom jednej cechy średnich warunkowych drugiej. Jej reprezentacją graficzną jest „empiryczna linia regresji”, która powstaje poprzez połączenie punktów o współrzędnych:
Przybliżeniem funkcji regresji I rodzaju jest funkcja regresji II rodzaju, np. liniowa y = ax + b
Badanie związków cech jakościowych
Tablica kontyngencji
Miarą siły związku jest statystyka di-kwadrat:
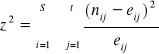
,
gdzie: ![]()
to tzw. liczebności teoretyczne,
ponadto: ![]()
Przyjmuje ona wartość z przedziału:
![]()
przy czym:
„0” oznacza niezależność stochastyczną cech „X” i „Y”
![]()
związek funkcyjny
Miara ta jest trudna do interpretacji, ponieważ jest nieunormowana, tj. jej wartość rośnie wraz ze wzrostem liczby kolumn i wierszy (wariantów wartości cech) oraz liczebności próby. Zwykle zakłada się, że liczebności empiryczne nie są mniejsze niż 5 dla każdej komórki w tabeli.
Miary unormowane
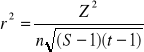
<0,1>
0 - oznacza niezależność stochastyczną
1 - oznacza zależność funkcyjną
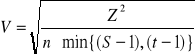
<0,1>
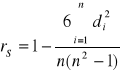
<-1,1>
di - oznacza różnicę między rangami odpowiadającymi wartościom cech „X” oraz „Y”
(di = xi - yi)
Analiza dynamiki (badanie zmian w czasie)
Szereg czasowy
y1, y2, y3,…, y4
yt to wartość badanej cechy w okresie lub momencie „t”
Wskaźniki dynamiki (indeksy)
![]()
gdzie:
yt to wartość cechy w okresie badanym
y0 to wartość cechy w okresie bazowym, podstawowym (branym jako punkt odniesienia)
i > 100% oznacza wzrost wartości cechy w okresie badanym w porównaniu z okresem podstawowym o: i - 100%
i = 100% oznacza brak zmian w okresie badanym w porównaniu z okresem podstawowym
i < 100% oznacza spadek wartości cechy w okresie badanym w porównaniu z okresem podstawowym o: 100% - i
Rodzaje indeksów:
![]()
![]()
Średnie tempo zmian
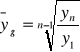
jeżeli: ![]()
to oznacza przeciętny wzrost
![]()
to oznacza przeciętny spadek
WIG - Warszawski Indeks Giełdowy
Od 1993r jego wartość jest liczona według formuły kapitałowej:
![]()
gdzie:
t oznacza badany okres (sesję giełdową)
M(t) wartość rynkowa (kapitalizacja) wszystkich spółek notowanych na giełdzie
K(0) kapitalizacja wszystkich akcji w dniu 16.04.1991r (I sesja giełdy), która wynosiła 57 140 000 starych złotych
K(t) współczynnik korygujący dla okresu badanego (uwzględnia dywidendy i pobory)
Indeksy Indywidualne
![]()
![]()
![]()
![]()
Indeksy Zespołowe (Agregatowe)
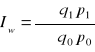
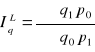
mówi o przeciętnym wzroście (spadku) ilości określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że cena w okresie badanym była na poziomie z okresu podstawowego (cena stała z okresu podstawowego)
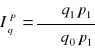
mówi o przeciętnym wzroście (spadku) ilości określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że cena w okresie podstawowym była na poziomie z okresu badanego (cena stała z okresu badanego)
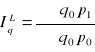
mówi o przeciętnym wzroście (spadku) cen określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym, przy założeniu, że ilość w okresie podstawowym była na poziomie z okresu badanego
![]()
mówi o przeciętnym wzroście (spadku) ilości określonego zbioru wyrobów w okresie badanym w porównaniu z okresem podstawowym
![]()
mówi o przeciętnym wzroście (spadku) cen określonych zbiorów wyrobów w okresie badanym w porównaniu z okresem podstawowym.
Wahania sezonowe
Zmiany zjawisk zależą także od działania czynników o charakterze sezonowym. Źródłem tych zmian jest cykl przyrodniczy (pory roku rolnictwo), technologiczny (budownictwo), instytucjonalny (budżet), zwyczajowy (moda ubrania).
Aby wyodrębnić działanie czynników sezonowych obliczamy tzw. Wskaźniki sezonowości za pomocą jednej z dwóch formuł:
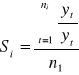
gdzie:
![]()
oznacza wartość trendu dla okresu „t”
![]()
liczba wystąpień i-tego okresu (kwartału, itp.)
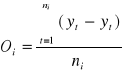
![]()
absolutna wielkość wahań sezonowych (to nie jest wskaźnik)
W praktyce jednak trudno ocenić rodzaj wahań (tylko na podstawie wykresu), stąd najczęściej przyjmuje się model multiplikatywny.
Jeśli spełnia się zależności:
![]()
lub ![]()
to oznacza to, że wskaźniki sezonowości są „czyste”, tj. wolne od wahań przypadkowych. W przeciwnym wypadku, w każdym z nich należy zastosować współczynniki korygujące:
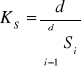
lub 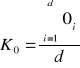
Korekty dokonujemy odpowiednio:
![]()
lub ![]()
gdzie:
![]()
oraz ![]()
„surowe” wskaźniki sezonowości
Wahania przypadkowe (losowe)
Na zmiany zjawisk wpływają czynniki losowe (przypadkowe), które można wyodrębnić porównując rzeczywistą wartość badanej cechy „y”, z jej teoretyczną wartością skorygowaną o wahania sezonowe:
![]()
lub
![]()
Wpływ wahań losowych można ocenić za pomocą wariancji:
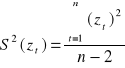
Kiedy przygotowana jest prognoza na podstawie posiadanego modelu zmian w czasie, należy oszacować przewidywaną wielkość wahań losowych za pomocą wzoru:
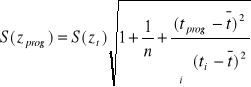
gdzie:
n długość szeregu czasowego
tprog numer okresu, dla którego dokonywana jest prognoza
Praca pochodzi z serwisu www.e-sciagi.pl
1
![]()
Xmin
Xmax
25%
25%
25%
25%
Q1
Me
Q3
![]()
![]()
![]()
Me
Me
D
D
ni
ni
xi
xi
Lewostronna
Prawostronna
Symetria
xi
ni
D
Me
![]()
xi
xi
ni
ni
Skrajna Asymetria Prawostronna
Skrajna Asymetria Lewostronna
![]()
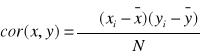
pamiętając o odpowiedniej liczebności próby
r=1
r=+0,76
r=+0,14
r=-0,69
Korelacje prostoliniowe
r=0
r=0
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
statystyka-krótki rys historyczny (9 str), ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
podstawowe pojęcia statystyka, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
statystyka - prawdopodobienstwo, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
Statystyka - Zadanie TV, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
Statystyka matematyczna - wzory, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
statystyka.23, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
STATYSTYKA - analiza korelacji i regresji, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
STATYSTYKA - trend liniowy, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
Statystyka - teoria, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
statystyka-definicje (3 str), ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
statystyka 1, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
STATYSTYKA - szereg czasowy, ŚCIĄGI Z RÓŻNYCH DZIEDZIN, Statystyka
więcej podobnych podstron