Cel æwiczenia :

1.Zapoznaie cwicz¹cych z metod¹ pomiaru wspó³czynnika przewodnoœci cieplnej izolatorów

2.nabycie umiejêtnoœci obs³ugi ultratermostatu

3.dokonanie pomiaru wsp³óczynnika przewodnoœci ciplnej izolatorów.

Wprowadzenie teoretyczne:

Przewodnictwo cieplne polega na przenoszeniu energii w postaci ciep³a w kierunku obszarów o ni¿szej temperaturze, a wiêc polega na d¹¿eniu uk³adu do wyrównania temperatury. Opisuje to prawo Foureira:

iQ - gêstoœæ strumienia enegii (ciep³a)

- przewodnoœæ cieplna w³aœciwa

T - temperatura

Je¿eli w wyniku pewnych warunków przeciw³egle scianki pewnej p³yty o powierzchni przekroju S i gruboœci d1, maja odpowiednio temperatury T1 i T2 (T1>T2), to nastepuje przep³yw ciep³a w kierunku powierzchni o ni¿szej temperaturze.

Iloœæ ciep³a przep³ywaj¹cego w jednostce czasu w stanie stacjonarnym wyra¿a siê wzorem :

gdzie:

- k - wspó³czynnik przewodnoœci cieplnej, oznacza iloœæ ciep³a przechodz¹cego w jednostce czasu przez jednostkê powierzchni przy jednostkowym gradiencie temperatury (ro¿nica temperatury 1K przypada na jednostkê gruboœci).

Ró¿ne cia³¹ maj¹ ró¿ne wartoœci przewodnoœci cieplnej. Cia³a o ma³ej wartoœci wspó³czynnika przewodnoœci cieplnej
nazywaj¹ siê izolatorami termicznymi. Badana p³ytka, której wspó³czynnik przewodnoœci cieplnej k nale¿y wyznaczyæ, jest okr¹g³a, w zwi¹zku z czym zale¿noœæ mo¿na napisac w postaci:

r1 - promieñ badanej p³ytki

Aby wyznaczyæ wspó³czynnik przewodnoœci cieplnej p³ytki, nale¿y zmerzyæ jej gruboœæ d1, promieñ r1, temperatury T1 i T2 przeciwleg³ych powierzchni oraz iloœæ ciep³a Q przechodz¹c¹ w jednostce czasu miêdzy powierzchniami o tych temperaturach.

Ta iloœæ ciep³a jest bezpoœrednio trudna do zmierzenia, dlatego te¿ wyznacza siê j¹ poœrednio metod¹ stygniêcia. Uk³ad do wyznaczania przewodnoœci cieplnej sk³ada siê z puszki mosie¿nej o grubym dnie P1, p³ytki mosiê¿nej P2, p³ytki badanej P oraz ultratermostatu Hopplera.

Puszka, p³ytka badana i mosiê¿na s¹ okr¹g³e. Mosiê¿na p³ytka P2 opiera siê na trzech izoluj¹cych nó¿kach, na niej jest po³o¿ona badana p³ytka a nastêpnie mosiê¿na puszka. Z ultratermostatu po³¹czonego przewodami gumowymi jest ogrzewana puszka P1 , a nastêpnie ciep³o jest przewodzone przez p³ytkê P do p³yty P2. W dnie puszki oraz w mosiê¿nej p³ytycie znajduj¹ siê termometry w metalowych oprawkach. Uk³ad p³yt ogrzewa siê do momentu ustalenia temperatury T1 górnej p³yty (puszki) i temperatury T2 dolnej p³yty. Mo¿na wówczas przyj¹æ, ¿e temperatura górnej powierzchhni badanej p³ytki rowna jest temperaturze T1 puszki, a temperatura dolnej powierzchni badanej p³ytki jest równa temperaturze T2 dolnej p³yty mosiê¿nej. Ustalenie siê temperatur zachodi wówczas, gdy iloœæ ciep³a przewodzona przez badan¹ p³ytkê jest równa iloœci ciep³a wypromieniowanej przez doln¹ p³ytê. Aby okreœilæ tê iloœæ ciep³a, nale¿y wyznaczyæ szybkoœæ stygniêcia dolnej p³ytki w pobli¿u temperatury T2. W tym celu po wyjêciu badanej p³ytki, ogrzewa siê doln¹ p³ytê do temperatury o kilka stopni wy¿szej od T2 a nastêpnie po zdjêciu puszki wyznacza siê szybkoœæ jej stygniêcia.W jednakowych odstêpach czasu (co 30 sek.) mierzy siê temperaturê do chwili, gdy temperatura dolnej p³yty bêdzie o kilka stopni ni¿sza ni¹ T2.

Przebieg ch³odzenia nale¿y przedstawiæ graficznie odk³adaj¹c na osi rzêdnych temperatury T, a na osi odciêtych czas t. Z wykresu mo¿na okreœliæ szybkoœæ stygniêcia
w pobli¿u temperatury T2.

Je¿eli szybkoœæ stygniêcia jest n, to iloœæ wypomieniowanego ciep³a w jednostce czasu jest równa mcn , przy czym m oznacza masê mosiê¿nej p³ytki c - ciep³o w³aœciwe mosi¹dzu.

Zak³adaj¹c, ¿e iloœæ wypromieniowanego ciep³a jest proporcjonalna do powierzchni, mo¿na wyraziæ iloœæ ciep³¹ wypromieniowan¹ przez jednostkê powierzchni w jednostce czasu jako

gdzie

r- promieñ mosie¿nej p³ytki

d- gruboœæ mosiê¿nej p³ytki

Uwzglêdniwszy fakt, ¿e po ustaleniu siê temperatur iloœæ ciep³¹ przewodzona przez badan¹ p³ytkê jest równa iloœci ciep³a wypromieniowanej przez boczn¹ i doln¹ powierzchniê mosiêznej p³yty, mo¿na napisaæ

st¹d wzór obliczeniowy:

Za³o¿enie proporcjonalnoœci wypromieniowanego ciep³a do wielkoœci powierzchni jest pewnym przybli¿eniem.

Czêœæ pomiarowa:

1. P³yn w ultratermostacie ogrzany do temp. 82 `C

2.Temperatury równowagi:

-dla p³yty plaskikowej 38.3 `C

-dla p³yty ebonitowej 16.1`C

3. Okreœlenie szybkoœci stygniêcia poszczególnych p³yt

p³yta plastkiowa p³yta ebonitowa

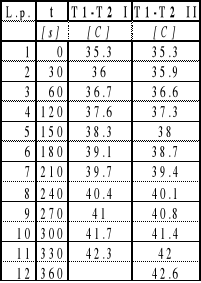
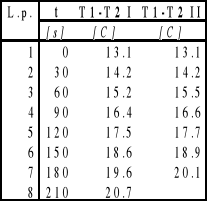
4.Pomiary wspó³czynnika n dla p-któw:

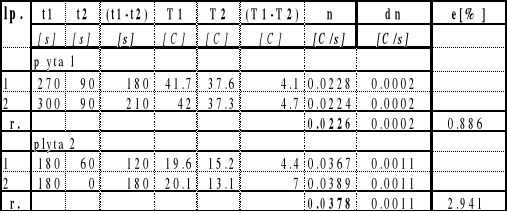
p³yta 1 p³yta 2

n=0.02260.0002 [K/s] n=0.03780.0011 [K/s]

5. Pomiary œrednicy i gruboœci p³yty mosiê¿nej oraz badanych p³yt:

Dok³adnoœæ suwmiarki 0.02 [mm]

Dok³adnoœæ œruby 0.01 [mm]

P³yta mosiê¿na:

Numer	średnica P2		d - grubość P2	
pomiaru	[mm]	[mm]	[mm]	[mm]
1	150.14	0.027	11.89	0.092
2	150.16	0.007	11.85	0.052
3	150.20	0.033	11.69	0.108
4			11.76	0.038
5			11.80	0.002
Wartość średnia	150.167	0.023	11.798	0.059
	0.015		0.500

r=75.0840.012 [mm] d=11.7980.059 [mm]

P³yty plastikowa ebonitowa

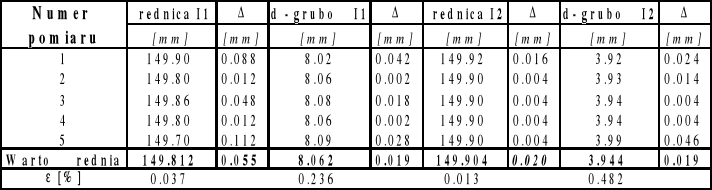
r=74.9060.028 [mm] r=74.9520.01 [mm]

d=8.0620.019 [mm] d=3.9440.019 [mm]

6.Sta³e przyjête do obliczeñ:

c=37540 [J/kg/K] m=1.6990.002 [kg]

7.Wzory obliczeniowe :

kplastik=0.0976

kebonit=0.1897

b³¹d bezwzglêdny:

plastik ebonit

	c/c [%]	10.667	10.667
	m/m[%]	0.118	0.118
	n/n[%]	0.886	2.941
	d1/d1[%]	0.236	0.482
	r1*2/r1[%]	0.073	0.009
D	T/T[%]	2.611	2.611
D	[%]	0.053	0.053
	k/k[%]	14.643	16.881

kplastik=0.09760.0143 [J/(msK)] kebonit=0.18970.0320 [J/(msK)]

=14.643 [%] =16.881 [%]

8.Wnioski:

Dokonywaliœmy pomiaru wspó³czynnika przewodnoœci cieplnej izolatorów.

Jako izolatory s³u¿y³y kr¹¿ki z plastiku (przeŸroczystego) i ebonitu.

Bardzo du¿y b³ad bezwzglêdny wnosi sta³a ciep³a w³aœciwego mosi¹dzu.

W przypadku pomiaru œrednicy p³yty ebonitowej b³¹d wzglêdny mia³ mniejsz¹ wartoœæ od dok³adnoœci suwmiarki. Przyjêto, wiêc jako b³¹d dok³adnoœci suwmiarki.

---