19-21

Pole elektryczne - pole fizyczne, stan przestrzeni w której na ładunek elektryczny działa siła. Pole to opisuje się przez natężenie pola elektrycznego lub potencjał elektryczny.

Koncepcję oddziaływania ładunków elektrycznych poprzez pole elektryczne wprowadził Michael Faraday.

Definicja

Natężenie pola elektrycznego jest parametrem pola wektorowego
, definiowanym jako stosunek siły
działającej na ładunek elektryczny q znajdujący się w tymże polu elektrycznym do wartości tegoż ładunku elektrycznego q:

Ładunek z pomocą którego określa się pole, zwany ładunkiem próbnym, musi spoczywać i być na tyle mały, by nie zmieniać układu ładunków w otaczajacej przestrzeni.

Własności

Pole elektryczne jest polem potencjalnym a opisująca go funkcja to potencjał elektryczny. Związek między natężeniem pola elektrycznego
a jego potencjałem
wyraża się wzorem:

Punktowy ładunek elektryczny Q wytwarza pole, którego natężenie wyraża się wzorami:

lub

Wartość natężenia pola określa wzór:

gdzie:

• 
  - wektor wodzący, o początku w źródle pola, a końcu w rozważanym punkcie przestrzeni,

• 
  - wersor (wektor jednostkowy), o początku w źródle pola, a końcu w rozważanym punkcie przestrzeni.

Pole elektryczne jest nośnikiem energii, ilość energii jest proporcjonalna do kwadratu natężenia pola w jednostce objętości, zmienne pole elektryczne jest składnikiem fotonu. Statyczne pole elektryczne może być opisywane jako rozprzestrzenianie się wirtualnych fotonów.

Własności pola elektrycznego opisują równania Maxwella:

• Źródłem pola elektrycznego są ładunki elektryczne, linie sił zaczynają się i kończą na ładunkach - Pierwsze równanie, zwane prawem Gaussa dla elektryczności-pole elektryczne jest polem źródłowym.

• Zmienne w czasie pole magnetyczne wytwarza wirowe pole elektryczne -Drugie równanie, zwane prawem Faradaya.

• Zmienne pole elektryczne powoduje powstawanie pola magnetycznego, co określa czwarte równanie Maxwella.

• Pole elektrostatyczne jest polem bezwirowym.

Natężenie pola elektrycznego jest wielkości wektorową. Kierunek wektora E wskazuje kierunek siły działającej na ładunek dodatni umieszczony w tym punkcie. Wektory natężenia układają się w ciągłe linie, zwane liniami pola. Ich kształt zależy od rozkładu i wielkości ładunków wytwarzających pole.

Ładunek punktowy Q wytwarza pole o natężeniu E równym

Gdzie
, [ε₀- przenikalność prózni = 8.85*10^-12 F/m], r odległość punktu od ładunku. Jeśli w odległości r umieszczony zostanie inny ładunek q, to dozna on działanie siły
. Wzór ten nosi nazwę prawa Coulomba. Jeśli znaki obu ładunków są jednakowa, siła jest odpychająca, przy znakach przeciwnych przyciągająca. Siła o takiej wartości działa na każdy ładunek jednocześnie.

Analogicznie zachowuje się ładunek rozmieszczony równomiernie na kuli metalowej- jego natężenie na zewnątrz kuli jest takie samo, jakby był skoncentrowany w kuli. Natomiast wewnątrz kuli metalowej pola elektrycznego nie ma; E=0.

Pole elektryczne jest równe zeru wewnątrz metalu dowolnym kształcie. Spowodowane to jest obecnością swobodnych elektronów, które samorzutnie rozmieszczają się w taki sposób, by ich własne pole znosiło się całkowicie z polem zewnętrznym. Po osiągnięciu takiego stanu makroskopowy ruch elektronów zanika, co świadczy o braku pola elektrycznego.

Płytka (o powierzchni S) naładowana równomiernie ładunkiem Q wytwarza w swoim najbliższym otoczeniu pole o stałym natężeniu, równym

Układ dwóch płytek równoległych, naładowanych ładunkami Q oraz -Q. poza obszarem E=0, gdyż pola wytworzone przez obie płytki mają tę samą wielkość, lecz przeciwne znaki. W obszarze między płytkami pola dodają się, a jego natężenie wynosi:

Między płytkami pole jest jednorodne - ma stałą wartość i stały kierunek. Zaburzenia występują jedynie na brzegach układu i w dużej odległości od niego.

Potencjał pola elektrycznego

Praca związana z przeniesieniem ładunku jednostkowego w polu elektrycznym nazywa się potencjałem pola. Jest to wielkość względna, gdyż jej wartość odnosi się do pewnego wybranego punktu (lub obszaru), któremu przypisuje się potencjał zerowy. Potencjał V pola w danym punkcie r definiuje się jako pracę W sił zewnętrznych, potrzebną do przeniesienia ładunku jednostkowego z punktu o potencjale zerowym do tego punktu. Jeśli przeniesieniu ulega ładunek q , to
.

Ładunek punktowy Q. W tym przypadku za „punkt” odniesienia zwykle przyjmuje się nieskończoność. Wówczas potencjał V w punkcie odległym o r od ładunku wynosi
. Potencjał ładunku dodatniego jest dodatni, ujemnego - ujemny. Jeśli w odległości r umieszczony zostanie ładunek q, to jego energia potencjalna W (w polu ładunku Q) wynosi
Jest to zarazem energia ładunku Q w polu ładunku q. Jest to ich energia potencjalna ich wzajemnego oddziaływania. Identyczne wzory prawdziwe są i dla kul naładowanych równomiernie, o ile punkt r znajduje się na zewnątrz kuli.

Układ dwóch płytek równoległych oddalonych od wartość d. Jeśli potencjał płytki naładowanej ujemnie przyjmiemy za zerowy, to w obszarze płytki dodatniej potencjał wynosi
. Różnicę potencjałów między dwoma punktami nazywamy napięciem między tymi punktami i oznacza zwykle symbolem U. Tak więc: U=V₂ - V₁

Napięcie między okładkami kondensatora płaskiego wynosi więc U=V=Ed. Jednostką potencjały, a tym samym napięcia, jest wolt (V). odpowiada on takiej różnicy potencjałów, ze przeniesienie między nimi ładunku 1 kulomba wymaga pracy 1 dżula: 1V=1J/1C.

Linie sił

Kierunek pola E w przestrzeni można przedstawić za pomocą tzw. linii sił. Linie nie tylko pokazują kierunek E ale też jego wartość (liczba linii na jednostkę powierzchni).

Jeżeli liczbę linii przechodzących przez powierzchnię ΔS oznaczymy Δφ to wówczas

Δφ = E ΔS = EΔS cosα

gdzie α jest kątem pomiędzy wektorem powierzchni ΔS i wektorem E.

W ogólności więc

dφ = dE ds (18.3)

i jest to definicja strumienia elektrycznego.

Całkowity strumień przechodzący przez powierzchnię S można obliczyć jako sumę przyczynków od elementów powierzchni

Suma ta przedstawia całkę powierzchniową

(18.4)

Obliczmy teraz strumień dla ładunku punktowego w odległości r od niego.

W tym celu rysujemy kulę o promieniu r wokół ładunku Q i liczymy strumień (liczbę linii przez powierzchnię).

(18.5)

Otrzymany strumień nie zależy od r, a zatem strumień jest jednakowy dla wszystkich r. Całkowita liczba linii wychodzących od ładunku jest równa Q/ε₀ i linie te ciągną się do nieskończoności.

Ponieważ pokazaliśmy, że strumień jest taki sam przez każdą powierzchnię niezależnie od r więc jest to prawdą dla zamkniętej powierzchni o dowolnym kształcie (która otacza ładunek Q).

Taka powierzchnia nazywa się powierzchnią Gaussa.

Prawo Gaussa.

Prawo Gaussa służy do obliczania natężeń pochodzących od poszczególnych ciał. Aby posłużyć się prawem Gaussa należy wybrać dowolną powierzchnię zamkniętą wokół źródła (np. sferę).

Niech zamknięta powierzchnia obejmuje dwa ładunki Q₁ i Q₂. Całkowita liczba linii sił przecinająca powierzchnię zamkniętą wokół ładunków Q₁ i Q₂ jest równa

gdzie E₁ jest wytwarzane przez Q₁, a E₂ przez Q₂. Powołując się na wcześniejszy wynik otrzymujemy

φ_całk = (Q₁/ε₀) + (Q₂/ε₀) = (Q₁ + Q₂)/ε₀

Całkowita liczba linii sił jest równa całkowitemu ładunkowi podzielonemu przez ε₀. Podobnie można pokazać dla dowolnej liczby n ładunków.

Otrzymujemy więc prawo Gaussa

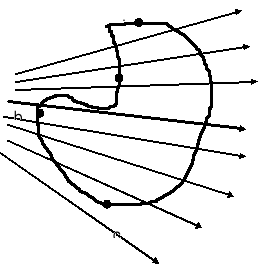
(18.6)

Strumień pola wychodzący z naładowanego ciała jest równa wypadkowemu ładunkowi podzielonemu przez ε₀. Jeżeli Q jest ujemne strumień wpływa do ciała.

Linie mogą zaczynać się i kończyć tylko na ładunkach a wszędzie indziej są ciągłe.

Prawo Coulomba:




Oznaczenia:
F_C - siła Coulomba;
k - stała elektrostatyczna;
Q - pierwszy ładunek;
q - drugi ładunek;
r - odległość pierwszego ładunku od drugiego; 

 - wersor (stosunek wektora do jego długości - pokazuje kierunek siły)

---