Tomasz Kowalski
Wykłady z matematyki dla studentów kierunków ekonomicznych
Wykład 24
CHARAKTERYSTYKI LICZBOWE ZMIENNYCH LOSOWYCH - lista zadań
Niech X będzie zmienną losową o rozkładzie danym za pomocą tabelki:
Dystrybuanta F zmiennej losowej X jest określona następującą tabelką:
Zmienna losowa X ma rozkład:
Zmienna losowa X ma rozkład:
Niech X będzie zmienną losową o rozkładzie danym za pomocą tabelki:
Eksperyment polega na trzykrotnym rzucie monetą. Zmienna losowa X jest różnicą między liczbą otrzymanych orłów a liczbą otrzymanych reszek. Wyznaczyć rozkład prawdopodobieństwa oraz dystrybuantę zmiennej X. Sporządzić wykres dystrybuanty. Obliczyć wartość oczekiwaną, wariancję oraz odchylenie standardowe.
Niech X będzie zmienną losową o gęstości
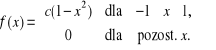
a) Wyznaczyć c, a następnie naszkicować wykres funkcji gęstości. b) Obliczyć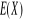
.Niech X będzie zmienną losową o gęstości
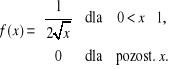
Obliczyć: a)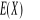
, b)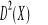
.Zmienna losowa X ma następującą gęstość prawdopodobieństwa:
Obliczyć wartość oczekiwaną i wariancję tej zmiennej.
Zmienna losowa X ma następującą gęstość prawdopodobieństwa:
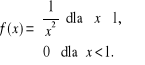
Wykazać, że zmienna ta nie posiada wartości oczekiwanej.
Zmienna losowa X ma następującą gęstość prawdopodobieństwa:
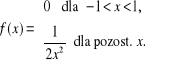
Naszkicować wykres gęstości. Wykazać, że zmienna ta nie posiada wartości oczekiwanej.
Zmienna losowa X ma dystrybuantę określoną wzorem:
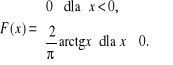
Naszkicować wykres dystrybuanty. Wyznaczyć gęstość i naszkicować jej wykres. Wykazać, że zmienna X nie posiada wartości oczekiwanej.
Zmienna losowa X ma następującą gęstość prawdopodobieństwa:
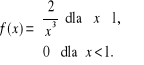
Obliczyć wartość oczekiwaną zmiennej X. Wykazać, że zmienna ta nie posiada wariancji.
Czy istnieje zmienna losowa X, dla której:
a)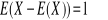
, b)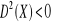
, c)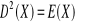
, d)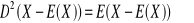
.
Dane są dwie niezależne zmienne losowe X i Y dla których:
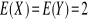
,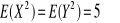
. Obliczyć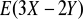
oraz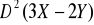
.
|
0 |
1 |
2 |
3 |
|
|
|
|
|
Sprawdzić, że jest to rozkład pewnej zmiennej losowej. Obliczyć wartość oczekiwaną zmiennej losowej X.
x |
(-∞, 1] |
(1, 3] |
(3, 6] |
(6, +∞) |
F(x) |
0 |
0,3 |
0,6 |
1 |
Wyznaczyć rozkład tej zmiennej losowej. Obliczyć wartość oczekiwaną.
|
-1 |
0 |
2 |
3 |
|
0,1 |
0,4 |
0,2 |
0,3 |
Wyznaczyć wartość oczekiwaną zmiennej losowej Y = 3X + 4, korzystając z odpowiednich własności wartości oczekiwanej.
|
-2 |
-1 |
0 |
1 |
2 |
|
0,25 |
0,2 |
0,1 |
0,2 |
0,25 |
Wyznaczyć wartości oczekiwane zmiennych losowych: a) X, b) Y = 3X + 4, c) ![]()
.
|
0 |
1 |
2 |
3 |
|
|
|
|
|
Obliczyć wartość oczekiwaną zmiennej losowej X, wariancję oraz odchylenie standardowe.
Odpowiedzi
1. ![]()
.
3. ![]()
, ![]()
. 4. a) ![]()
, b) ![]()
, c) ![]()
.
5. ![]()
, ![]()
, ![]()
.
![]()
, ![]()
, ![]()
.
7. a) ![]()
, b) ![]()
. 8. a) ![]()
, b) ![]()
. 9. a) ![]()
, b) ![]()
.
10. 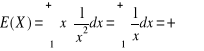
. 11. 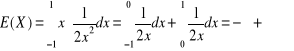
.
12. 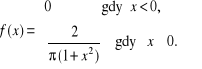
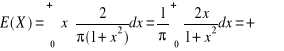
.
13. 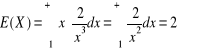
, 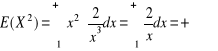
.
14. a) nie istnieje, ponieważ ![]()
dla każdej zmiennej losowej X.
b) nie istnieje, ponieważ ![]()
dla każdej zmiennej losowej X.
c) i d) istnieje np. X przyjmująca wartość 0 z prawdop. 1.
15. ![]()
, ![]()
.
2
Wykład 24: Charakterystyki liczbowe zmiennych losowych.
2.
|
1 |
3 |
6 |
|
0,3 |
0,3 |
0,4 |
![]()
x |
|
|
|
|
|
F(x) |
0 |
|
|
|
1 |
6.
|
|
|
1 |
3 |
|
|
|
|
|
Wyszukiwarka
Podobne podstrony:
726
Dz.U. 1997 nr 111 poz. 726 Tekst aktu
726
zal do decyzji nr 167, Załącznik do decyzji nr 726
726
test-726+odp najnowsze, geo i wycena
726
726
726
(Papermodels@eMule) [Modelik 1997 13 (Model Card 108)] Ssbn 726 Uss Ohio Rar
726 nowe pytania i odpowiedzi TM
Pytania nowe 726 i odpowiedzi dobre najnowsze, Geodezja, Uprawnienia
726
726
flash or repair Apollo 726 with Tracer OVO firmware and Apollo fix firmware
726 t freischneider oleomac
więcej podobnych podstron