1. Układy inercjalne i nieinercjalne, siła Coriolisa

Układy odniesienia znajdujące się w spoczynku lub poruszające się ruchem jednostajnym prostoliniowym względem układu inercjalnego są układami inercjalnymi. Natomiast układy poruszające się ze zmienną prędkością lub obracające się względem układu inercjalnego nazywamy układami nieinercjalnymi.

Układy w których obowiązuje I zasada dynamiki są układami inercialnymi

Zasada Galileusza wszystkie układy inercjalne są sobie równoważne każde zjawisko przebiega identycznie w dowolnym U.I. W układzie nie inercjalnym można stosować zasady dynamiki jeżeli uwzględnimy siłę unoszenia np.: siła bezwładności, odśrodkowa, Coriolisa. Układ związany z Ziemią jest U.NI. efektem tego jest siła coriolisa która działa na ciało poruszające się na powierzchni. Np.: niże na półkuli N kręcą się w lewo.

2. Elementy teorii względności

LORENTZ

Długość (kontrakcja)

Jeżeli w układzie odniesienia względem, którego ciało znajduje się w spoczynku, dł. ciała jest równa l₀ to w układzie odniesienia względem którego ciało porusza się z prędkością V długość ciała będzie równa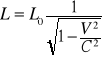

Wymiary poprzeczne nie ulegają skróceniu, skróceniu ulega tylko wymiar równoległy do kierunku ruchu.

Czas (dylatacja)

T(tau)=Δt=t₂-t₁

Jeżeli w układzie spoczynkowym odstęp czasowy między dwoma ciałami jest równy T₀ to odstęp czasowy między tymi zjawiskami w układzie odniesienia poruszającym się z prędkością jest równy

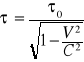
Masa

Jeżeli w układzie względem którego ciało jest w spoczynku masa ciała jest równa m₀ to w układzie odniesienia względem którego ciało porusza się z prędkością V jego masa jest równa

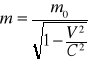
Energia

Całkowita energia ciała jest równa E=mC_­²

II zasada dynamiki w przypadku relatywistycznym

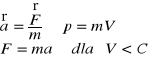
3. Zasady Dynamiki w przypadku klasycznym i relatywistycznym.

I zasada dynamiki

Jeżeli na ciało nie działa żadna siał lub wypadkowa działających sił jest równa zeru, to we wszystkich inercjalnych układach odniesienia ciało to będzie spoczywać lub poruszać się ruchem jednostajnym prostoliniowym.

II zasada dynamiki

Jeżeli na ciało o masie m zadziała siła F (lub wypadkowa kilku sił działających na ciało wynosi F), to ciało to będzie poruszać się z przyśpieszeniem proporcjonalnym do działającej siły a odwrotnie proporcjonalnie do masy ciała.

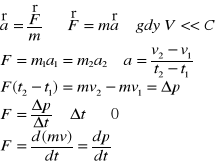
III zasada dynamiki

Jeżeli ciało A działa na ciało B siłą F_AB, to równocześnie na ciało A zadziała pochodząca od ciała B siła F_BA o tej samej wartości lecz o przeciwnym kierunku. F_AB=-F_BA

4. Podstawowe wielkości w ruchu obrotowym bryły sztywnej

Bryła sztywna - takie ciało, w którym odległości pomiędzy poszczególnymi jego elementami nie zmieniają się, niezależnie od działającej siły.

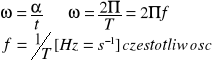
drogi liniowe s₁,s₂ są różne dla różnych pkt, prędkości liniowe też, natomiast równe są drogi kątowe i prędkości kątowe.

Droga kątowa jest to krąg zakreślony przez promień wodzący.

Prędkość kątowa jest wektorem, który jest równoległy do osi obrotu a jego zwrot określa śruba prawoskrętna. Związek między prędkością liniową i kątową.

5. Energia Kinetyczna w ruchu obr i zasada zachowania momentu pędu

Każde obracające się ciało posiada energię kinetyczną. Energia kinetyczna obracającego się ciała jest sumą energii kinetycznych poszczególnych jego elementów.

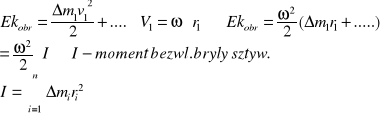
Momenty bezwł.

pkt materialny I=mr²

pierścień I=mr²

walec pełny I=1/2mr²

kula I=2/5mr²

pręt (oś prostopadła środek) I=1/12ml²

pręt (oś prostopadła początek) I=1/3ml²

Twierdzenie Steinera

Jeżeli moment bezwł. bryły sztywnej względem osi l przechodzącej przez środek masy jest równy l₀ to moment bezwł. tej bryły względem osi l' równoległej do l odległej od niej o d jest równy
l'||l

Moment siły

Zmiana prędkości kątowej ciała następuje pod wpływem działania momentów sił. Wartość momentu siły F definiuje się następująco: r-odległość pkt. przyłożenia od osi obrotu

Zasada zachowania momentu pędu.

Jeżeli moment sił zewnętrznych względem danej osi obrotu jest równy zeru, to moment pędu ciała (lub układu ciał) względem tej osi jest stały.

gdy M=0 to L=const. I₁ω₁=I₂ ω₂

6. Pole grawitacyjne

Pr. grawitacji Newtona

2 ciała przyciągają się siłą, która jest wpros proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między nimi.

G-stała grawitacji G=6,67*10^-11 [Nm²/kg²]

Prawo grawitacji zapisane wektorowo:

W każdym pkt pola grawitacyjnego można zdefiniować wielkość wektorową, oznaczającą siłę grawitacji działającą na jednostkę masy- Natężenie pola grawitacyjnego

Natężenie pola grawitacyjnego nie zależy od masy ciała m a zależy tylko od masy M będącego źródłem pola.

Linie sił pola grawitacyjnego wskazują w przestrzeni wokół źródła kierunek siły grawitacji jaka zadziała na ciało m umieszczone w danym polu.

Przyśpieszenie w polu grawitacyjnym

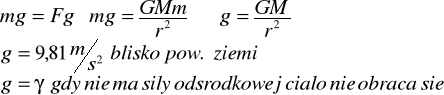
7. Prawo Keplera

1 prawo Keplera - wszystkie planety poruszają się po elipsach, w jednym z 2 ognisk elipsy znajduje się Słońce. P-perychelium (pkt najbliższy słońcu) A-adchelium (pkt najdalej oddalony od słońca)

I uogólnione prawo Keplera- wszystkie ciała niebieskie poruszają się po krzywych stożkowych. W ogniskach tych krzywych znajduje się gwiazda.

II prawo Keplera - prędkość polowa planety jest stała. Prędkośc polowa jest polem zakreślonym w jednostce czasu przez promień wodzący planety. Im dalej planeta od słońca tym wolniej się porusza.

II uogólnione prawo Keplera- moment pędu planety jest stały. Pęd to iloczyn masy i prędkości planety.

p=mV L=Pr L=mVr - const v₁r₁=v₂r₂

III prawo Keplera Drugie potęgi okresów obiegu planet wokół słońca (T₁,T₂) są wprostproporcionalne do trzecich potęg wielkich półosi (a₁,a₂)

III uzgodnione prawo Keplera- wszystkie ciała układu słonecznego poruszają się po elipsach wokół wspólnego środka masy

8. Ruch harmoniczny

Ruch harmoniczny- ruch w którym przyśpieszenie jest wprostproporcionalne do wychylenia i skierowane do położenia równowagi. A-amplituda drgań, x- położenie cząstki C po czasie t ω- częstość drgań, f- częstotliwość drgań /ilość drgań w 1s/ T- okres drgań/czas 1 drgania/

Związek pom. ruchem har. a ruchem po okręgu- Cząstka C₁ porusza się po okręgu o promieniu A o środku w pkt O ze stałą prędkością kątową ω.T-okres obrotu, f-częstot. obrotu

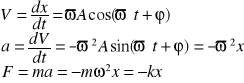
9. Drgania tłumione

W przyrodzie występują siły tarcia, które zmniejszają siłę drgań dlatego w realnych ośrodkach występują drgania tłumione a nie harmoniczne

A'=A₀e ^-Bt i B-stała tłumienia

Aby otrzymać drgania harmoniczne /o stałej amplitudzie A/ trzeba uzupełniać straty energii w każdym okresie

Energia drgań

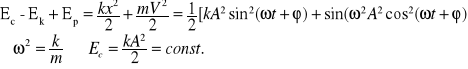
Podczas drgań harmonicznych następuje ciągła przemiana Ek w Ep i odwrotnie ale zawsze suma tych energii pozostaje stała.

10. Wahadło fizyczne i matematyczne

Wahadłem fizycznym nazywamy bryłę sztywną zawieszoną na osi obrotu nie przechodzącą przez środek masy

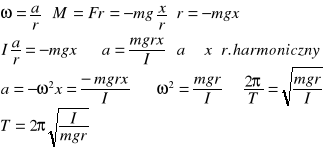
O-środek obrotu, S-środek ciężkości

wahadło matematyczne- pkt materialny zawieszony na nieważkiej i nierozciągliwej nici.

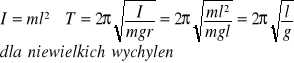
11. Pole elektrostatyczne

P.elek.-przestrzeń, w której na ładunek elektryczny działa siła, miarą tego pola jest jego natężenie oraz indukcja elektryczna.

Natężenie pola elektrycznego- stosunek siły działającej na umieszczony w tym polu ład. próbny do jego wartości

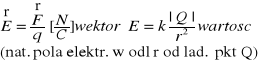
Pr. Coulomba: Dwa ładunki pkt odziaływują na siebie siłą, która jest wprostporpor. do iloczynu ich wartości i odwrotnie proporc. do kw. odległości między nimi.

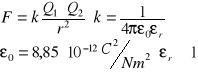
k-wsp. propor. zal. od ośrodka

ład. różnoimienne przyc., ład. równoimienne odpycha. rys.

Pr. Columba w zapisie wektorowym

ten sam rys.

Pr. Gaussa Całkowity strumień indukcji przechodzący przez dowolną pow. jest równy sumie ładunków znajdujących się wew. tej pow.

12. Praca w Polu elktr.

Praca w polu elektr. jest polem zachowawczym ponieważ praca w tym polu nie zależy drogi tylko od różnicy potencjałów.

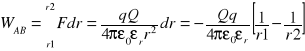
Potencjał pola elektrycznego w danym pkt nazywamy pracę którą wykona pole dla przesunięcia ładunku jednostkowego z tego pkt do nieskończoności albo jest to stosunek energii potencjalnej jaką ma ład. w tym pkt do jego wartości.

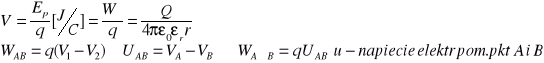
W_AB -praca sił pola przy przesunięciu ładunku z pkt A do pkt B pola elektro.

q- przesuwany ładunek

Rozmieszczenie ładunków na przewodniku

Ładunek gromadzi się na zew. pow. przewodnika

13. Pojemność elektryczna

pojemność- określa zdolność przewodnika do gromadzenia ładunków elektrycznych. Stosunek ładunku do potencjału wytworzonego na przewodniku.

C=Q/V [farad]

Kondensatory są układami, które przy niewielkich rozmiarach mają b. dużą pojemność.

14. Prąd elektryczny

Jest to ruch swobodnych ładunków wywołany różnicą potencjałów

Natężenie prądu elektrycznego stałego

Jest to stosunek ładunku przepływającego przez poprzeczny przekrój przewodnika do czasu jego przepływu: I=Q/t [A]=[C/s] Ładunek ma wartość 1 Culomba, gdy przez przewodnik w czasie 1 sekundy przepłynie prąd o natężeniu 1 Ampera

Prawo Omha

Natężenie prądu zależy wprost proporcjonalnie od napięcia I=U/R Prawo Ohma jest spełnione tylko wtedy, gdy opór nie zależy od napięcia ani od natężenia prądu.

Praca prądu elektrycznego:

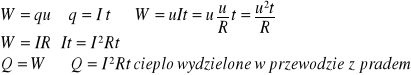
Moc prądu elektrycznego P=W/t [J/s]=[W]

Siła elektromotoryczna Miarą SEM ogniwa jest różnica potencjałów między elektrodami gdy nie czerpiemy prądu elektrycznego: E(epsilon)=W/Q [V]

I pr. Kirchoffa

Suma natężeń wchodzących do węzła sieci elektrycznej jest równa sumie natężeń prądów wychodzących z punktu węzłowego.

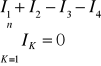
I₁+I₂-I₃-I₄=0

II Pr. Kirchoffa

Jeżeli w obwodzie prądu albo zamkniętej części obwodu, przyjmiemy jako dodatni kierunek zgodny z ruchem wskazówek zegara to suma iloczynów natężeń i oporów gałęzi będzie równa sumie sił elektromotorycznych znajdujących się w tym obwodzie

15. Pole magnetyczne

P.mg przestrzeń, w której na biegunie magnetycznym działa siła, biegunów nie da się rozdzielić.

Pr. Gausa dla magnetyzmu:

Całkowity strumień indukcji magnetycznej przez dowolną pow. zamkniętą jest równy 0. zawsze ilość linii pola magnetycznego wychodzących z pow. zamkniętej będzie równa ilości linii sił wchodzących.

Pole magnetyczne prądu elek. Oersted odkrył: przewodnik z prądem wytwarza pole mag., linie sił tego pola są okręgami współśrodkowymi z tym przewodnikiem. Zwrot ich określa reguła śruby prawoskrętnej.

H=I/2Пr [A/m] pole mag. przewodnika prostoliniowego niesk. długiego.

H=I/2r pole mag przewodnika kołowego.

H=Ni/l n-ilość zwoii, I- natężenie, l-dł.

Siła elektrodynamiczna jest to siła, która działa na przewodnik z prądem umieszczony w polu magnetycznym

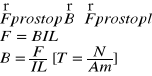
16. Falowa i kwantowa teoria światła

---