POLITECHNIKA LUBELSKA w LUBLINIE
LABORATORIUM PODSTAW ELEKTROTECHNIKI		Ćwicz. nr 4
TEMAT: Analogie polowe i obwodowe.		DATA: 1997.03. 20
WYKONAŁ: Dariusz Bober	GRUPA: ED 4.4	OCENA:

Skład grupy: Kopacz Piotr, Dubiel Marek, Bober Dariusz

Cel ćwiczenia: Poznanie związków i analogii teorii obwodów elektrycznych z teorią pola elektromagnetycznego .

1. Schemat układu pomiarowego.

Spis przyrządów :

V --- cyfrowy nr 6746

mA --- magnetoelektryczny kl.0.5 zak. 3000mA nr 43-3/1470 , nr 1603062.79 i nr43.3/589

V--- elektromagnetyczny kl. 0.5 zak. 30V nr 43-3-793

At --- autotransformator R1, R2, R3 --- oporniki suwakowe R4, R5 ---elementy silitowe

Wyznaczanie natężenia pola elektrycznego E_t , gęstości prądu wewnątrz przewodnika i mocy czynnej obwodu .

Tabela pomiarów 1

I1 [mA]	I2 [mA]	I3 [mA]
100	100	200

Tabela pomiarów 2

	I [mA]	U [V]	P [W]
R1	100	0,227	0,028
R2	100	0,074	0,009
R3	200	0,301	0,074

Przykład obliczeń : P.=1.23*I_śr*U_śr

P.=1.23*0.2A*0,301 V=0,074W

Tabela pomiarów 3

Lp	ΔU	Et	J	p	P	Δl
-	[V]	[V/m.]	[A/mm^2]	[W/m^3]	[W]	[cm]
1-2	0,00167	0,0334	1,99732	66,71	2,62E-06	5
2-3	0,00183	0,0366	2,18868	80,106	3,14E-06	5
3-4	2,04	40,8	0,027336	1115,309	9,85E-03	5
4-5	0,22	4,4	0,002948	12,971	1,15E-04	5
5-6	0,22	4,4	0,002948	12,971	1,15E-04	5
6-7	0,0044	0,088	5,2624	463,091	1,82E-05	5
7-8	0,0021	0,042	2,5116	105,487	4,14E-06	5
8-9	0,00206	0,0412	2,46376	101,507	3,98E-06	5
9-10	0,00206	0,0412	2,46376	101,507	3,98E-06	5
10-11	0,00206	0,0412	2,46376	101,507	3,98E-06	5
1'-2'	0,00109	0,0218	0,22454	4,895	4,32E-7	5
2'-3'	0,00124	0,0248	0,25544	6,335	5,59E-7	5
3'-4'	0,37	7,4	0,004958	36,689	3,24E-04	5
4'-5'	0,22	4,4	0,002948	12,971	1,15E-04	5
5'-6'	0,15	3	0,00201	6,03	5,33E-05	5
6'-7'	0,0238	0,476	4,9028	2333,733	2,06E-04	5
7'-8'	0,0119	0,238	2,4514	583,433	5,15E-05	5
8'-9'	0,0119	0,238	2,4514	583,433	5,15E-05	5
9'-10'	0,0116	0,232	2,3896	554,387	4,9E-05	5
10'-11'	0,0115	0,23	2,369	544,87	4,81E-05	5

_cu = 59.8 S*m. / mm²

_Fe=10,3 S*m/mm²

_{elementów silitowych}=0,67*10^-3 S*m/mm²

Przykład obliczeń: E_t=U/l składowa styczna natężenia pola elektrycznego

E_t= 0,00183V/5cm = 0.0366 V/m

J = *E_t gęstość prądu

J = 59.8 S*m./mm² * 0,0366 V/m = 2,18868 A/mm²

p.= * E_t² gęstość objętościowa mocy

p.= 59.8 S*m./mm² * (0.0366 V/cm ²)² = 80,106 W/mm³

P.= p.*V = p.* * (d/2)²*l moc czynna

P.=66,7mW/mm³ * [3.14*(1/2)² *50]mm³= 0,000 003 14 W

Tabela pomiarów 4:

	1-1'	2-2'	3-3'	4-4'	8-8'	9-9'	10-10'	11-11'	12-12'	13-13'	14-14'	15-15'
U [V]	11,23	11,23	11,11	-	11,23	11,13	11,13	11,13	11,13	11,13	11,13	11,13
En [V/cm]	1,123	1,123	1,123	-	1,123	1,113	1,113	1,113	1,113	1,113	1,113	1,113

l = 10 cm

E_n = U /l składowa normalna natężenia pola elektrycznego

E_n = 11,23V / 10cm = 1,123 V/cm

2 a . Sprawdzenie prawa Ohma w postaci różniczkowej.

Obliczam rezystancję dla odcinka obwodu 2-3.

R=U_2-3/ I₃ = 1,83mV/200mA = 9,15m

Na podstawie teorii polowej sprawdzamy różniczkowe prawo Ohma : J = * E_t

Równoważne równanie możemy zapisać następująco R'= /

R' = [E_t *l] / [J * 3,14 * (d / 2)²

R' = [0,0366*10³ V/cm * 5cm] / [2,18868A/mm² * 3,14 * 0,25mm² ] = 10,6m

Jak widać wartości rezystancji obliczone przy pomocy teorii polowej i obwodowej różnią się nieznacznie co potwierdza prawdziwość różniczkowego prawa Ohma.

2 b . Sprawdzenie równania Laplace'a .

Równanie sprawdzimy na odcinku 1-4 obwodu .

Ponieważ zmiana potencjału występuje tylko wzdłuż osi X równanie Laplace'a uprości się do postaci d²/ dx² = 0

Całkując dwukrotnie otrzymamy = C₁ * x + C₂

By wyznaczyć stałe całkowania zakładamy że punkt 3 jest uziemiony i jego potencjał jest równy 0.

By wyznaczyć stałą całkowania C₂ obliczamy wartość potencjału w punkcie 1 dla X=0

(0) = C₂ = 1,67+1,83 = 3,5mV

Stałą całkowania C₁ obliczamy wiedząc ,że potencjał w punkcie 3 wynosi 0 .

0 = C₁ * 10 cm + 3,5mV

C₁ = -3,5/10 mV/cm

Możemy teraz równanie potencjału zapisać w postaci:

= -3,5/10 mV/cm * x + 3,5 mV

Otrzymaliśmy zależność zmian potencjału od odległości od punktu w którym

=0.

Sprawdzając ją w naszym przypadku dowodzimy prawdziwość równania Laplace'a .

Wyznaczanie rozkładu pola elektrycznego ,wykreślenie linii ekwipotencjalnych i wektorów pola E wzdłuż współrzędnych X i Y .

Rys2 Rozkład pola elektrycznego wokół dwóch przewodów. Linie ekwipotencjalne oE = 0.4 V

Przykład obliczeń wektora E₀ = U / l ^. 1_st

E₀ = (6V - 4V) / [1.5cm - (-1.5cm)] ^. 1_st

E₀ = [(2 / 3) V/cm] ^. 1_st

Wnioski.

- Rozpatrywanie obwodu elektrycznego za pomocą teorii pola daje te same rezultaty , które uzyskuje się rozpatrując za pomocą teorii obwodów elektrycznych , możemy zatem potwierdzić i udowodnić podstawowe prawa dotyczące pól elektrycznych stacjonarnych .

- Pole stacjonarne przepływowe jest polem bezwirowym i bezźródłowym co można wywnioskować z równań które to pole spełnia : div J = 0 rot E = 0 . Wobec tego można napisać zależność natężenia pola elektrycznego i potencjału w postaci E = - grad V.

-W ćwiczeniu nie wykorzystywaliśmy elementów silitowych w związku z czym sprawozdanie nie zawiera charakterystyki U=f(l) dla tych elementów. Charakterystyka dla całego obwodu przedstawia się następująco:

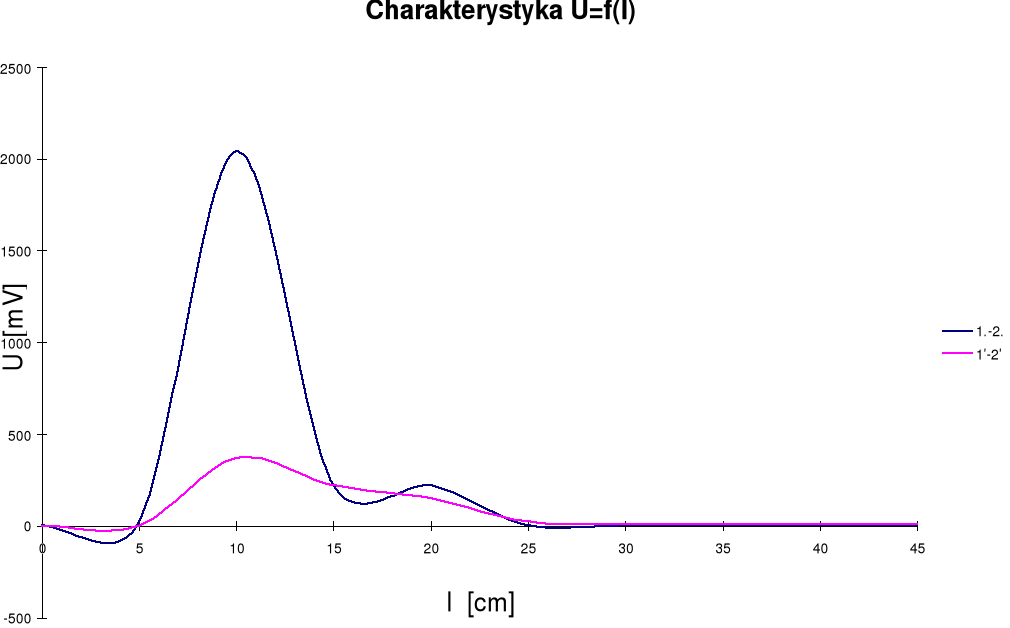
- Widać tutaj że największy spadek napięcia występował na granicy przewodu miedzianego i pręta zbudowanego z żelaza, pomiędzy 5-15 cm. Ten odcinek obwodu grzał się najbardziej.

---