Wykład 2. Opisowa analiza zjawisk masowych

1. Rozkładem empirycznym zmiennej nazywamy przyporządkowanie kolejnym wartościom zmiennej (
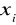
   ) odpowiadających im liczebności (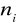
   ).

Rozkład odzwierciedla strukturę zbiorowości.

Przykład: Jeżeli zbiorowością statystyczną są rodziny (n=150), a cechą mierzalną skokową liczba dzieci (X) w rodzinie, to w rezultacie pogrupowania danych indywidualnych (
=0,1,2,3,4,5) otrzymujemy empiryczny (punktowy) rozkład tej cechy(zmiennej).

Liczba dzieci ( )	Liczba rodzin ( )
0	15
1	62
2	43
3	25
4	3
5	2
Ogółem	150

3. Rodzaje rozkładów empirycznych

Przykład: Zaprezentować graficznie różne typy rozkładów empirycznych dla cechy skokowej i ciągłej.

4. Charakterystyki rozkładów

Najczęściej wykorzystywane charakterystyki przy opisie struktury zbiorowości to:

• Miary średnie( inaczej położenia, przeciętne) służą do określenia tej wartości zmiennej opisanej przez rozkład, wokół której skupiają się wszystkie pozostałe wartości zmiennej;

• Miary rozproszenia (zmienności, zróżnicowania, dyspersji) służą do badania stopnia zróżnicowania wartości zmiennej;

• Miary asymetrii (skośności) służą do badania kierunku zróżnicowania wartości zmiennej;

• Miary koncentracji służą do badania stopnia nierównomierności rozkładu lub do analizy stopnia skupienia poszczególnych jednostek wokół średniej.

Miary średnie

Średnia arytmetyczna:

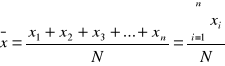
lub

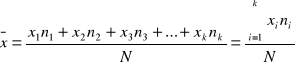
a w przypadku obliczeń procentowych

,

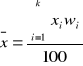
gdzie

Przykład:

Wyznaczyć średnią arytmetyczną ilości punktów uzyskanych z egzaminu testowego z wiedzy teoretycznej ze statystyki w grupie studentów socjologii.

Otrzymano następujące wyniki:

Ilość uzyskanych punktów z testu	Liczba studentów	Obliczenia pomocnicze
20-30 30-40 40-50 50-60 60-70 70-80	2 10 7 9 12 10	25 35 45 55 65 75	50 350 315 495 780 750	4,0 20,0 14,0 18,0 24,0 20,0	100,0 700,0 630,0 990,0 1560,0 1500,0
Razem	50	X	2740	100,0	5480,0

czyli

.

Średnia harmoniczna (stosujemy ją wówczas, gdy wartości zmiennej podane są w jednostkach względnych, np. w km/godz.; kg/osobę itp.):

W przypadku szeregu wyliczającego

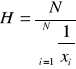
lub w przypadku szeregu rozdzielczego

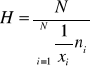
Przykład: Załóżmy, że gęstość zaludnienia w dwu 100 tyś miastach wynosi odpowiednio: 500
i 700
.Jaka jest przeciętna gęstość zaludnienia obu tych miast?

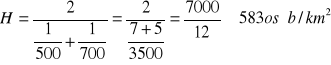
Średnia geometryczna (stosujemy w przypadku badania średniego tempa zmian zjawisk, czyli w analizie dynamiki zjawisk):

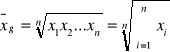
Dominanta (modalna, wartość najczęstsza) - w szeregach wyliczających i rozdzielczych punktowych dominanta to wartość cechy o największej liczebności. W szeregach rozdzielczych przedziałowych można określić przedział, w którym znajduje się dominanta tzn. przedział o największej liczebności. Wartość dominanty należącą do tego przedziału wyznaczamy ze wzoru:

gdzie

- dolna granica klasy, w której znajduje się dominanta,

- liczebność przedziału dominanty,

- liczebność przedziału poprzedzającego przedział dominanty,

- liczebność przedziału następującego po przedziale dominanty,

- rozpiętość przedziału dominanty.

Graficzna metoda wyznaczania dominanty:

Np.

3 5 D 7 9

Kwantyle (kwartyle, kwintyle, decyle, percentyle) - wartości cechy badanej zbiorowości, które dzielą ją na określone części pod względem liczby jednostek.

Uwaga:

W celu wyznaczenia kwantyli szeregi statystyczne muszą być uporządkowane tzn. rosnąco lub malejąco!

Najczęściej wykorzystuje się kwartyle:

• Kwartyl pierwszy(dolny)-dzieli zbiorowość w ten sposób, że 25% jednostek ma wartości niższe, a 75% ma wartości wyższe od kwartyla pierwszego.

• Mediana czyli kwartyl drugi-dzieli zbiorowość w ten sposób, że 50% jednostek ma wartości niższe oraz 50% ma wartości wyższe od mediany.

• Kwartyl trzeci(górny)-dzieli zbiorowość w ten sposób, że 75% jednostek ma wartości niższe, a 25% ma wartości wyższe od kwartyla trzeciego.

Do wyznaczania kwartyli wykorzystujemy wzory:

Mediana dla szeregu wyliczającego:

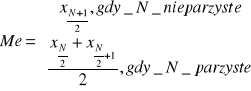
W przypadku szeregów rozdzielczych przedziałowych:

Kwartyl pierwszy:

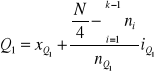
Mediana:

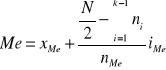
Kwartyl trzeci:

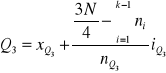
gdzie

- dolne granice przedziałów, w których znajdują się odpowiednio kwartyl pierwszy, mediana, kwartyl trzeci,

N- ogólna liczebność danej zbiorowości,

- suma liczebności od klasy pierwszej do tej, w której znajdują się odpowiednio kwartyl pierwszy, mediana, kwartyl trzeci,

- liczebności przedziałów, w których znajdują się odpowiednio kwartyl pierwszy, mediana, kwartyl trzeci,

- rozpiętości przedziałów, w których znajdują się odpowiednio kwartyl pierwszy, mediana, kwartyl trzeci.

Przykład: Empiryczne badanie liczby punktów uzyskanych w teście na inteligencję przez 56 uczennic i 56 uczniów pewnej klasy gimnazjalnej dostarczyło dane, które zapisano w postaci szeregu rozdzielczego:

Wyniki testu w punktach	Liczba uczniów
		Dziewczęta	Chłopcy
20-40 40-60 60-80 80-100 100-120 120-140	1 4 17 25 8 1	1 4 11 19 13 8
Ogółem	56	56

Wyznaczyć średnie pozycyjne (dominantę, kwartyl pierwszy, medianę, kwartyl trzeci) dla grupy dziewcząt oraz chłopców.

Rozwiązanie dla grupy dziewcząt:

W celu wyznaczenia kwartyli należy w pierwszej kolejności dokonać kumulacji liczebności:

Wyniki testu w punktach	Liczba dziewcząt	Skumulowane częstości
20-40 40-60 60-80 80-100 100-120 120-140	1 4 17 25 8 1	1 5 22 47 55 56
Ogółem	56	X

• Skoro
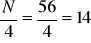
  czyli przedział [60-80] jest przedziałem klasowym, w którym znajduje się kwartyl pierwszy, czyli:

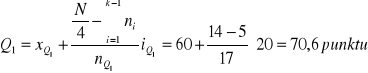
• Skoro
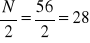
  czyli przedział [80-100] jest przedziałem klasowym, w którym znajduje się mediana, czyli:

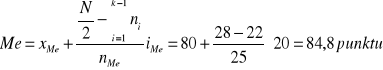
• Skoro
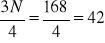
  czyli przedział [80-100] jest przedziałem klasowym, w którym znajduje się kwartyl trzeci, czyli:

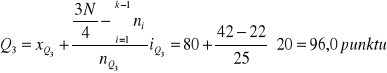
Podobne obliczenia dla grupy chłopców dają wyniki (sprawdzić w domu !):

D=91,4 punktu, Me=92,6 punktu,
=76,4 punku,
=110,8 punku.

Miary rozproszenia (zmienności, zróżnicowania, dyspersji) służą do badania stopnia zróżnicowania wartości zmiennej.

Pozycyjne miary zmienności:

• Empiryczny obszar zmienności:

• Odchylenie ćwiartkowe

Uwaga: Do określenia typowego obszaru zmienności można wykorzystać odchylenie ćwiartkowe oraz medianę tzn.

Klasyczne miary zmienności:

• Odchylenie przeciętne określa, o ile wszystkie jednostki danej zbiorowości różnią się średnio od średniej arytmetycznej rozpatrywanej zmiennej.

Dla szeregu wyliczającego:

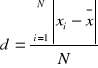
Dla szeregu rozdzielczego:

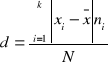
• Wariancja to średnia arytmetyczna z kwadratów odchyleń poszczególnych wartości cechy od średniej arytmetycznej całej zbiorowości.

Dla szeregu wyliczającego:

Dla szeregu rozdzielczego:

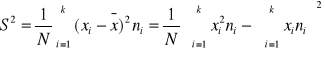
Odchylenie standardowe to pierwiastek kwadratowy z wariancji, czyli

Uwaga: Odchylenie standardowe można wykorzystać do budowy typowego obszaru zmienności cechy, tzn.:

• Współczynnik zmienności, który informuje o sile dyspersji. Duże wartości liczbowe świadczą o niejednorodności zbiorowości. Współczynnik zmienności obliczamy w różny sposób w zależności od rodzaju wykorzystywanych miar przeciętnych, tzn.:

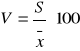
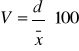
Przykład: Empiryczne badanie liczby punktów uzyskanych w teście na inteligencję przez 56 uczennic i 56 uczniów pewnej klasy gimnazjalnej dostarczyło dane, które zapisano w postaci szeregu rozdzielczego:

Wyniki testu w punktach	Liczba uczniów
		Dziewczęta	Chłopcy
20-40 40-60 60-80 80-100 100-120 120-140	1 4 17 25 8 1	1 4 11 19 13 8
Ogółem	56	56

Dokonać oceny stopnia zróżnicowania wyników testu na inteligencję w populacji dziewcząt i chłopców(odchylenie standardowe, współczynnik zmienności, odchylenie przeciętne oraz odchylenie ćwiartkowe).

Rozwiązanie (dokonać niezbędnych obliczeń):

Wyniki	Dziewczęta	Chłopcy
S	18,43 punktu	23,92 punktu
V	22%	25,9%
d	14,9 punktu	18,9 punktu
Q	12,7 punktu	17,2 punktu

Otrzymane rezultaty oznaczają, że wyniki testu na inteligencję poszczególnych dziewcząt różnią się przeciętnie o 18,43 punktu w porównaniu ze średnim wynikiem (równym 83,6 punktu), analogiczne odchylenie wyników poszczególnych chłopców od ich wyniku średniego wynosi 23,92 punktu.

Współczynnik zmienności dla dziewcząt wynoszący 22% w porównaniu z analogicznym współczynnikiem dla chłopców wynoszącym 25,9% świadczy o tym, że subpopulacja dziewcząt jest mniej zróżnicowana niż subpopulacja chłopców.

W grupie chłopców odchylenie przeciętne wynosi 21 punktów i jest wyższe w porównaniu z grupą dziewcząt, natomiast odchylenie ćwiartkowe w rozkładzie chłopców jest niższe i wynosi 9,8 punktu.

Miary asymetrii (skośności)- oceniają, czy przeważająca liczba jednostek znajduje się powyżej, czy poniżej przeciętnego poziomu badanej cechy. Jeżeli rozkład jest symetryczny, to
(średnia arytmetyczna, mediana, dominanta są równe). Jeżeli
, to rozkład charakteryzuje się asymetrią prawostronną, jeżeli zaś
, to mamy do czynienia z lewostronną asymetrią rozkładu.

Najprostszą miarą asymetrii jest wskaźnik asymetrii:

Jeżeli W<0, to mamy do czynienia z asymetrią lewostronną. Jeżeli W>0, to występuje asymetria prawostronna.

Miarą określającą siłę i kierunek asymetrii jest współczynnik asymetrii(skośności):

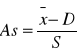
lub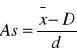

lub
,

gdzie
(
nazywamy momentem centralnym rzędu 3).

Miary te przyjmują wartości w przedziale [-1;1]. Gdy są dodatnie, to występuje asymetria prawostronna, gdy ujemne, to lewostronna.

Miary koncentracji- czyli skupienia:

,

gdzie

Dla rozkładu normalnego przyjmuje się, że
. Jeżeli
, to rozkład jest wysmukły. Jeżeli
, to rozkład jest spłaszczony.

Zadania do Wykładu 2:

Zad.1. Strukturę rodzin według liczby członków rodziny w miejscowości K charakteryzuje rozkład postaci:

Liczba członków rodziny	2	3	4	5	6	7	8
Odsetek rodzin	15	30	20	15	10	5	5

Za pomocą miar przeciętnych scharakteryzuj ten rozkład.

Odp.:

Zad.2. W jednym z domów akademickich przeprowadzono badanie dotyczące miesięcznych wydatków na cele kulturalne. Otrzymano następujące wyniki:

Odsetek studentów	10	30	40	20
Wydatki miesięczne w zł	40-80	80-120	120-160	160-200

Za pomocą klasycznych i pozycyjnych miar zmienności oceń zróżnicowanie badanej zbiorowości pod względem miesięcznych wydatków na cele kulturalne.

Odp.: V=28,12%

Zad.3. Dzienne zużycie energii elektrycznej (w kWh) w pewnym budynku mieszkalnym kształtowało się następująco:

Zużycie	2-4	4-6	6-8	8-10	10-12	12-14
Odsetek rodzin	6	10	30	40	10	4

Obliczyć miary tendencji centralnej oraz współczynnik zmienności. Wyznaczyć typowy obszar zmienności.

Odp.:

Zad. 4. Rozkład szkół podstawowych pod względem liczby uczniów przedstawia się następująco:

Liczba uczniów w szkole	0-40	40-80	80-120	120-160	160-200
Liczba szkół	10	60	70	65	100

Wyznaczyć
.

Zad.5. Dokonaj wszechstronnej analizy porównawczej struktury stażu pracy pracowników w dwóch przedsiębiorstwach na podstawie danych:

Staż pracy (w latach)	Liczba pracowników
		Przedsiębiorstwo A	Przedsiębiorstwo B
0-5 5-10 10-15 15-20 20-25 25-30 30-35 35-40 40-45	81 108 82 54 40 37 28 16 6	47 53 65 79 83 90 28 5 2

Odp.: Przedsiębiorstwo A:

Przedsiębiorstwo B:

33

Rozkłady empiryczne

cechy skokowej

cechy ciągłej

wielomodalne

jednomodalne

jednomodalne

wielomodalne

symetryczne

umiarkowanie asymetryczne

skrajnie asymetryczne

normalne

leptokurtyczne

platokurtyczne

prawoskośne

lewoskośne

Miary średnie

Średnie klasyczne:

• średnia arytmetyczna;

• średnia harmoniczna;

• średnia geometryczna

Średnie pozycyjne:

• dominanta(modalna, wartość najczęstsza;

• kwantyle (kwartyle, kwintyle, decyle, percentyle)

Pozycyjne miary zmienności:

- empiryczny obszar zmienności,

• odchylenie ćwiartkowe,

• współczynnik zmienności (liczony na podstawie miar pozycyjnych)

Klasyczne miary zmienności:

• odchylenie przeciętne,

• wariancja,

• odchylenie standardowe

Dyspersja (rozproszenie)

---