Kucaba Janusz 22.10.2005
I TD
Sprawozdanie z ćw. nr 21
Rozładowanie kondensatora
I. Zagadnienia do samodzielnego opracowania.
1. Pojemność elektryczna - definicja, rodzaje kondensatorów.
Pojemnością kondensatora nazywamy stosunek ładunku zgromadzonego na jednej z okładek do napięcia pomiędzy okładkami:
![]()
Kondensatory dzielą się na:
Płaskie, złożone z dwóch płyt, zwanych okładkami,
Kuliste, złożone z dwóch współśrodkowych metalowych kul,
Cylindryczne, złożone z dwóch współosiowych walców.
2. Ładowanie i rozładowanie kondensatora, równanie krzywej ładowania i rozładowania,
stała czasowa obwodu.
Ładowanie kondensatora następuje w układzie:
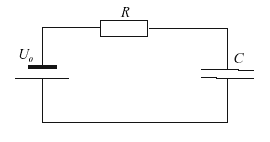
Ładowanie kondensatora polega na doprowadzeniu napięcia do jego okładek, co powoduje osadzanie się na nich ładunku elektrycznego. Na jednej z okładek gromadzi się ładunek dodatni, na drugiej ujemny.
Rozładowanie kondensatora następuje w układzie:

Rozładowanie kondensatora polega na podpięciu do nie go rezystora. Rezystor pozbawia kondensator ładunku, który osadził się na jego okładkach.
Równanie krzywej ładowania i rozładowania:
Prąd ładowania i rozładowania kondensatora wyraża się taką samą zależnością, tzn. że krzywe ładowania i rozładowania są identyczne i wyrażają się wzorem:
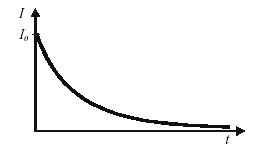
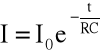
Stałą czasową obwodu nazywa się wielkość: = RC
Jest to taki czas po upływie którego prąd zmaleje e-krotnie.
3. Wyznaczanie pojemności kondensatora na podstawie jego krzywej rozładowania.
Pojemność kondensatora na podstawie krzywej rozładowania można wyznaczyć na kilka sposobów:
Gdy t= to:
Dla czasu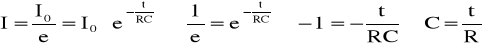
, wartość natężenia prądu jest równa I = I0/e, korzystając z wykresu krzywej rozładowania odczytujemy czas i korzystając ze wzoru C=/R obliczamy pojemność kondensatora.
Obliczamy wartość ładunku Q. i korzystając ze wzoru: C = Q/U obliczamy pojemność kondensatora.
4. Wyznaczanie wartości ładunku zgromadzonego na okładkach kondensatora na podstawie krzywej
rozładowania.
Wartość ładunku można obliczyć z wyznaczenia wartości pola powierzchni zawartego między osiami układu współrzędnych a wykresem krzywej rozładowania.
II. Wykonanie Ćwiczenia
Połączyć układ wg. schematu. Odczytać wartość oporu z opornicy dekadowej.
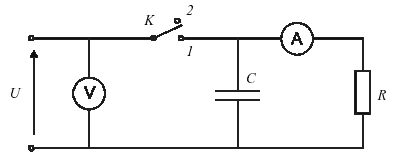
Naładować kondensator, gdy wartość prądu ustali się przyjąć ją jako I0 dla chwili t = 0 (s).
Przełączyć przełącznik P i jednocześnie włączyć sekundomierz. Przeprowadzić pomiary natężenia prądu rozładowania
kondensatora I = f(t).Sporządzić wykres prądu rozładowania : I = f(t) oraz wykres
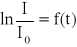
.Wyznaczyć pojemność kondensatora :
![]()
gdzie : Q - wartość ładunku zgromadzonego na okładkach kondensatora,
U - napięcie między okładkami, które w tym przypadku jest równe napięciu zasilającemu obwód pomiarowy.
Obliczyć stałą czasową obwodu korzystając z wykresu
![]()
III. Wynik Pomiarów
U [V] |
R [kΩ] |
I0 [μA] |
t [s] |
I [μA] |
Q [μC] |
C [μF] |
[s] |
5 |
33 |
150 |
1,57 |
140 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
2,5 |
130 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
3,82 |
120 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
5,42 |
110 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
7,09 |
100 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
8,82 |
90 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
10,75 |
80 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
12,95 |
70 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
15,76 |
60 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
19,06 |
50 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
22,8 |
40 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
27,45 |
30 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
34,8 |
20 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
46,38 |
10 |
2602,4 |
520,5 |
17,18 |
5 |
33 |
150 |
127,67 |
0 |
2602,4 |
520,5 |
17,18 |
IV. Obliczenia:
Wyznaczyć pojemność kondensatora:
Ładunek zgromadzony na okładkach kondensatora wyznaczamy licząc pole powierzchni pod krzywą I = f(t) jako sumę pól trapezów wyznaczonych przez punkty pomiarowe.
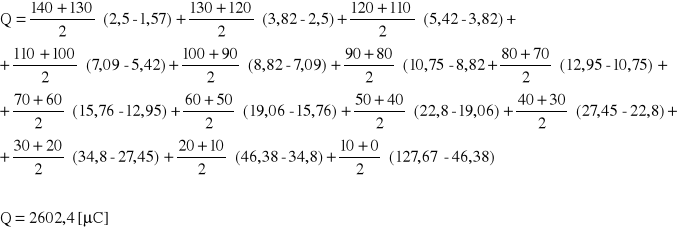
Pojemność Kondensatora:
![]()
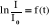
Współczynnik nachylenia prostej :
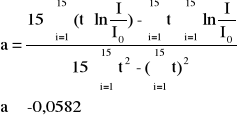
Stała czasowa obwodu:
![]()
Stała czasowa obwodu = R C jest równa wartości bezwzględnej z odwrotności współczynnika nachylenia prostej
możemy ją także obliczyć znając rezystancję R i pojemność C:
![]()
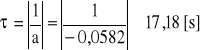
V. Rachunek błędów:
Błąd pomiaru napięcia:
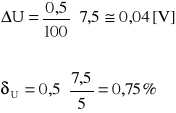
![]()
Błąd pomiaru prądu:

Błąd pomiaru czasu:
Błąd bezwzględny pomiaru czasu określamy jako czas reakcji wykonującego pomiar:
![]()
Błąd względny :

Błąd w obliczeniach ładunku:
Ładunek zgromadzony na okładkach kondensatora obliczamy jako sumę pól trapezów :
![]()
gdzie i = 1,2,..15 ( punkty pomiarowe ), więc całkowity ładunek obliczamy jako
![]()
Błąd bezwzględny :
ostatecznie:
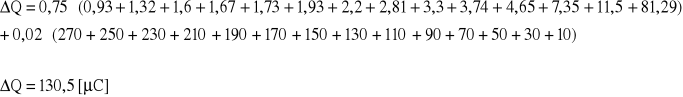
Błąd względny:
![]()
Błąd w obliczeniach pojemności:
bezwzględny : ![]()
ostatecznie
![]()
względny : ![]()
![]()
VI. Wnioski:
Pojemność badanego kondensatora C = 520,5 30,3 F,
stała czasowa = 17,18 s.
Stała czasowa obliczona ze wzoru ![]()
niewiele się różni od wyznaczonego metodą najmniejszych kwadratów co świadczy o dobrych obliczeniach pojemności.
Wyznaczanie pojemności w sposób przedstawiony w ćwiczeniu jest dość kłopotliwe, gdyż czasochłonne jest obliczanie ładunku zgromadzonego w kondensatorze jako pola pod krzywą rozładowania I = f(t).
![]()
![]()
![]()
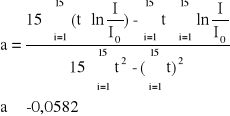
![]()
![]()
![]()
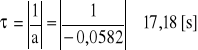
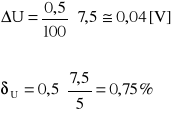

![]()

Wyszukiwarka
Podobne podstrony:
Wyznaczanie stałej siatki dyfrakcyjnej, Prz inf 2013, I Semestr Informatyka, Fizyka, SPRAWOZDANIA DU
SiS strona tytulowa spr, Prz inf 2013, I Semestr Informatyka, Fizyka, Wykłady-Fizyka, Sygnały i Syst
Tabela pomiarowa, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare
tabele 1B+, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, 1b
ćw 23, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, Fizyka Dam
Ćwiczenie nr 44 prawie dobre ale juz teraz lux, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA
ćw 1 obliczenia, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
spr5, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, bartochowsk
obliczenia ćw23, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
Ćwiczenie nr 44, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
Wstęp teoretyczny ćw 44, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium
pierwsza strona sprawozdania własne, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki,
pierwsza strona sprawozdania, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laborat
Ćwiczenie 47, Prz inf 2013, I Semestr Informatyka, Fizyka, SPRAWOZDANIA DUZO, laboratorium
sprawko1bwstę pteoretyczny, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laborator
więcej podobnych podstron