Wydział Budownictwa Studia dzienne

Lądowego i Wodnego

Politechnika Wrocławska

ĆWICZENIE PROJEKTOWE

Z PODSTAW KONSTRUKCJI BETONOWYCH

Projektowanie elementów betonowych

BELKA

Dane początkowe:

- Beton: B25

- Stal: AI

- stopeiń zbrojenia:

1. Zestawienie obciążeń (na podstawie PN-82/B-02000).

Obciążenia	Wartość charakterystyczna	Współczynnik obciążenia γf		Wartość obliczeniowa
				max	min	max	min
		[kN/m]	[-]	[-]	[kN/m]	[kN/m]
Płyty granitowe 0,02m	0,56	1,1	0,9	0,62	0,50
Gładź wyrównawcza 0,03m						0,63	1,3	0,8	0,82	0,50
Płyta z wełny mineralnej trwałej 0,05m						0,1	1,2	0,9	0,12	0,09
Płyta żelbetowa 0,15m						3,75	1,1	0,9	4,13	3,75
Tynk cementowy 0,03m						0,63	1,3	0,8	0,82	0,50
		RAZEM:		6,51	5,34

Obciążenia stałe:

[kN/m]

[kN/m]

[kN]

Obciążenia zmienne:

[kN/m]

[kN]

2. Obciążenie belki.

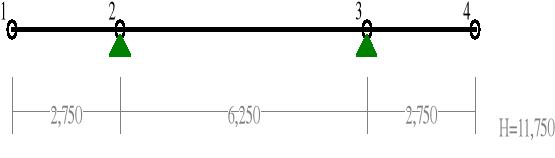
I schemat obciążenia

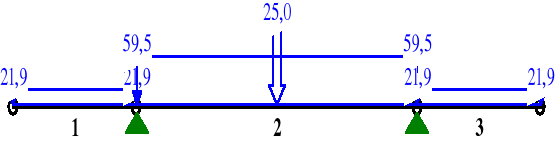
MOMENTY:

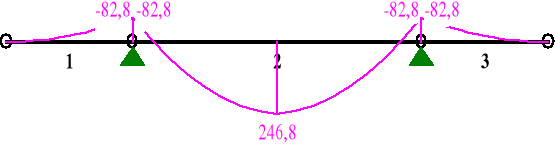
TNĄCE:

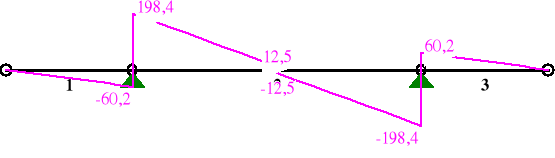
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,0 0,0 0,0

1,00 2,750 -82,8 -60,2 0,0

2 0,00 0,000 -82,8 198,4 0,0

0,50 3,125 246,8* 12,5 0,0

1,00 6,250 -82,8 -198,4 0,0

3 0,00 0,000 -82,8 60,2 0,0

1,00 2,750 0,0 0,0 0,0

------------------------------------------------------------------

* = Wartości ekstremalne

II schemat obciążenia

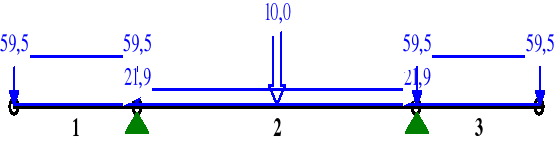
MOMENTY:

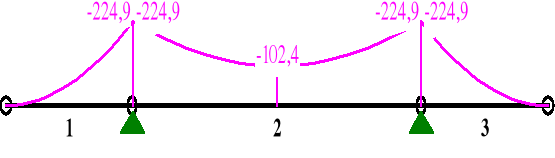
TNĄCE:

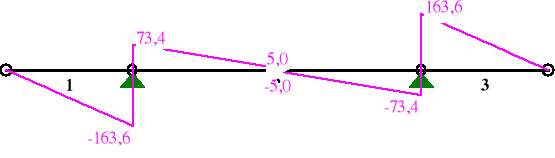
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 -0,0 0,0 0,0

1,00 2,750 -224,9 -163,6 0,0

2 0,00 0,000 -224,9 73,4 0,0

0,50 3,125 -102,4* 5,0 0,0

1,00 6,250 -224,9 -73,4 0,0

3 0,00 0,000 -224,9 163,6 0,0

1,00 2,750 0,0 0,0 0,0

------------------------------------------------------------------

* = Wartości ekstremalne

3. Wymiarowanie przekroju.

b_eff

h_f

h d

A_s1

b_w

3.1. Użyteczna wysokość przekroju.

gdzie:

l_eff - rozpiętość obliczeniowa (11,75 m);

a_lim - graniczna wartość ugięcia (z tab.8 PN-B-03264:2002) = 0,03m;

d - użyteczna wysokość przekroju.

→

m

przyjmuje d = 0,7 m = 700 mm

3.2. Szerokość środnika.

gdzie:

V_sd - maksymalna siła tnąca [kN];

- wytrzymałość obliczeniowa betonu na ściskanie [MPa];

d - użyteczna wysokość przekroju [m];

kN

→
m

przyjmuje b_w = 0,2 m

3.2. Szerokość półki.

gdzie:

b_eff - szerokość półki [m];

M_max - maksymalny moment [kNm];

A = 0,774 [MPa] (tab.10 dla
).

kNm

m

→
→

warunek jest spełniony

Przyjęte wymiary przekroju:

h = 0,74 m

d = 0,70 m

b_eff = 0,71 m

b_w = 0,20 m

h_f = 0,10 m

4. Wyznaczanie obwiedni momentów.

4.1. Ciężar belki

gdzie:

A - pole przekroju teowego [m²];

- ciężar objętościowy betonu zbrojonego sprężonego (z tab. 25 kN/m³).

m²

kN/m

kN/m

4.2. Wykresy sił przekrojowych.

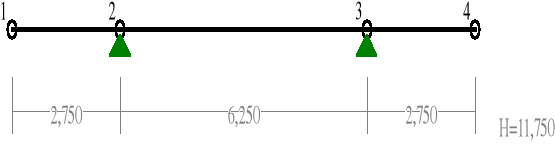
I schemat obciążenia

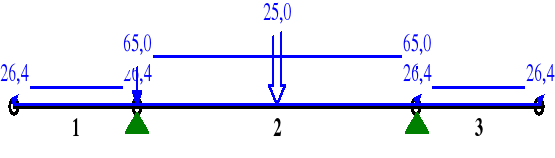
MOMENTY:

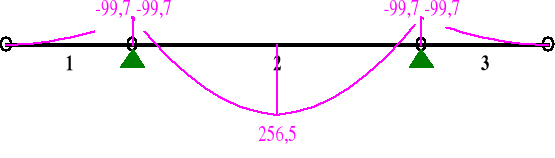
TNĄCE:

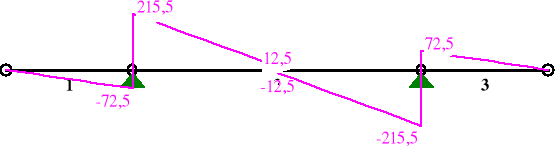
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,0 0,0 0,0

1,00 2,750 -99,7 -72,5 0,0

2 0,00 0,000 -99,7 215,5 0,0

0,50 3,125 256,5* 12,5 0,0

1,00 6,250 -99,7 -215,5 0,0

3 0,00 0,000 -99,7 72,5 0,0

1,00 2,750 0,0 0,0 0,0

------------------------------------------------------------------

* = Wartości ekstremalne

II schemat obciążenia

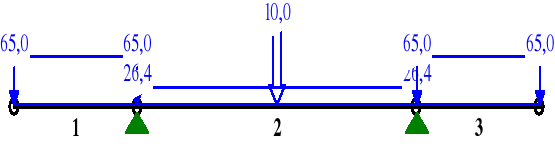
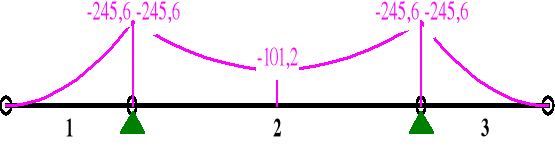
MOMENTY:

TNĄCE:

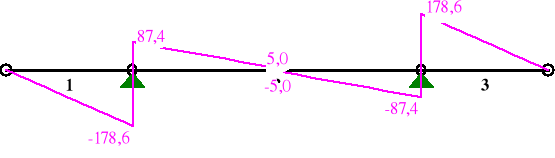
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,0 -0,0 0,0

1,00 2,750 -245,6 -178,6 0,0

2 0,00 0,000 -245,6 87,4 0,0

0,50 3,125 -101,2* 5,0 0,0

1,00 6,250 -245,6 -87,4 0,0

3 0,00 0,000 -245,6 178,6 0,0

1,00 2,750 0,0 0,0 0,0

------------------------------------------------------------------

* = Wartości ekstremalne

4.3. Obwiednia momentów.

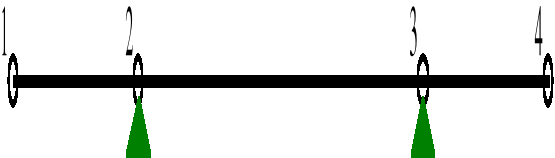
5. Wymiarowanie przekroju ze względu na zginanie.

5.1. Sprawdzanie teowości przekroju.

gdzie:

= 13,3 MPa = 13300 kPa

d = 0,70 m

b_eff = 0,71 m

h_f = 0,10 m

kNm

Przekrój jest pozornie teowy

5.1. Wymiarowanie w przęśle.

kNm

MPa x

MPa

m

m M A_S1

A

→ x_1eff = 1.3600 m

x_2eff = 0.0399 m

m

(dla stali AI
) warunek jest spełniony

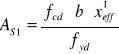
Przyjmuje 5 prętów
22 (A_s = 19,01)

5.2. Wymiarowanie na podporze.

kNm

MPa A_S2

MPa

m M x

m

→ x_1eff = 1.2526 m

x_2eff = 0.1474 m

m

(dla stali AI
) warunek jest spełniony

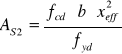
Przyjmuje 5 prętów
22 (A_s = 19,01)

6. Długość zakotwienia prętów.

MPa

MPa

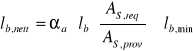
gdzie:

- współczynnik efektywności zakotwienia (dla prętów prostych
);

- podstawowa długość zakotwienia [mm];

- minimalna długość zakotwienia [mm];

- pole przekroju zbrojenia wymaganego zgodnie z obliczeniami;

- pole przekroju zbrojenia zastosowanego.

→
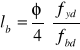
mm

≥
lub
(dla prętów rozciąganych)

<
mm → przyjmuje:

przyjmuję:

7. Ścinanie.

7.1. Podpora A z lewej strony (wspornik).

II I

7.1.1. Rozstaw strzemion.

kN - odczytano z wykresu l_t2 l_t1

l_t 0,250

przyjmuje:
ponieważ

kN

Ponieważ
jest to odcinek II rodzaju, a co za tym idzie, konieczne jest policzenie zbrojenia na ścinanie.

Długość odcinka II rodzaju:

Stal przeznaczona na strzemiona ST3SX (AI):

MPa

MPa

MPa

Ponieważ siła tnąca nie jest zbyt duża (
) mogę zastosować strzemiona pionowe.

Dziele odcinek na mniejsze:

W związku z tym ze cały odcinek l_t ma 1,413 m i po podzieleniu go na 2 odcinki ten drugi będzie bardzo mały, dlatego przyjmę w nim rozstaw strzemion taki jak w odcinku pierwszym.

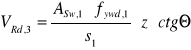
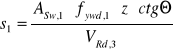
przyjmując:

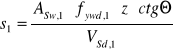
gdzie:

- pole przekroju poprzecznego prętów tworzących jedno strzemię prostopadłe do osi elementu. Dla pręta
→
;

- obliczeniowa granica plastyczności strzemion prostopadłych do osi elementu dla stali AI = 210 MPa;

z =
;

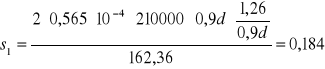
m

Przyjmuje:

Rozstaw strzemion na lewym wsporniku na odcinku II rodzaju wynosi 18 cm. W pozostałej części wspornik będzie zbrojony konstrukcyjnie (rozstaw strzemion:
→
)

7.1.2. Sprawdzanie nośności.

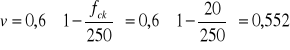
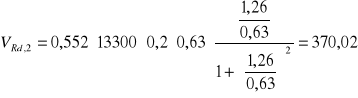
kN

7.2. Podpora A z prawej strony (przęsło).

7.2.1. Rozstaw strzemion.

kN - odczytano z wykresu

I II

l_t1 l_t2

0,250 l_t

przyjmuje:
ponieważ

kN

Ponieważ
jest to odcinek II rodzaju, a co za tym idzie, konieczne jest policzenie zbrojenia na ścinanie.

Długość odcinka II rodzaju:

Stal przeznaczona na strzemiona ST3SX (AI):

MPa

MPa

MPa

Ponieważ siła tnąca nie jest zbyt duża (
) mogę zastosować strzemiona pionowe.

Dziele odcinek na mniejsze:

a co za tym idzie:

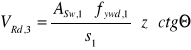
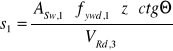
przyjmując:

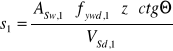
gdzie:

- pole przekroju poprzecznego prętów tworzących jedno strzemię prostopadłe do osi elementu. Dla pręta
→
;

- obliczeniowa granica plastyczności strzemion prostopadłych do osi elementu dla stali AI = 210 MPa;

z =
;

Dla I odcinka:

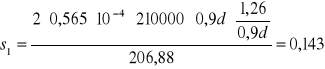
m

Przyjmuje:

Dla II odcinka:

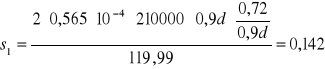
m

Przyjmuje:

Rozstaw strzemion na przęśle jest identyczny po prawej i po lewej stronie. Na odcinku drugiego rodzaju (1,98m) strzemiona rozstawione są co 14 cm, natomiast w środku przęsła na długości 2,04m strzemiona rozmieszczone są konstrukcyjnie, czyli co 0,4 m.

7.1.2. Sprawdzanie nośności.

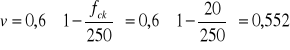
Dla I odcinka:

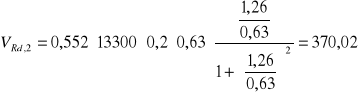
kN

Dla II odcinka:

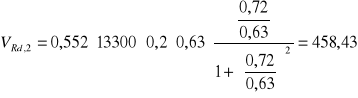
kN

---