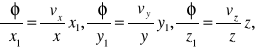Ruch elementu płynu

W kinematyce ciała sztywnego dowodzi się, że w ogólnym przypadku ruch ciała sztywnego składa się w każdej chwili z ruchu postępowego i obrotowego dokoła pewnej osi, zwanej chwilową osią obrotu. Ruch płynu jest znacznie bardziej skomplikowany, ponieważ każdy element płynu porusza się nie tylko ruchem postępowym i obrotowym, lecz podlega również odkształceniu (deformacji). Ostat­nie zjawisko wymaga zatem zbadania tak zwanego ruchu deformacyjnego.

Rozpatrzmy w dowolnej chwili ruch nieskończenie małego elementu płynu. Niech w pewnym punkcie M (x, y, z) wewnątrz elementu (rys. 1) składowymi prędkości będą v_x(x, y, z), v_y(x, y, z), v_z(x, y, z).

Rys. 1

Składowe prędkości w pewnym punkcie M₁(x+x₁, y+y₁, z+z₁) na powierzchni elementu mogą być wówczas na­pisane w postaci

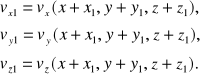
Wykorzystując rozwinięcie na szereg Taylora i zachowując jedynie wielkości małe pierwszego rzędu, czyli człony zawierające x₁, y₁, z₁ w potędze nie wyższej niż pierwsza, otrzymamy następujący wzór na prędkości v_x1, v_y1, v_z1:

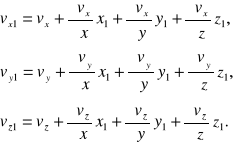
(1)

w których dla uproszczenia podstawiono v_x=v_x(x, y, z), v_y=v_y(x, y, z), v_z=v_z(x, y, z). Przekształćmy teraz te wzory. W tym celu dodamy do prawej strony pierwszego równania (1) wielkości

oraz

dokonamy przegrupowania wyrazów.

Ostatecznie otrzymamy

skąd

Za pomocą analogicznych przekształceń można z drugiego i trzeciego równania (1) otrzymać

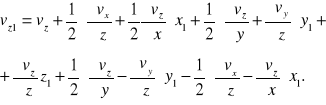
Dla uproszczenia wprowadźmy oznaczenia:

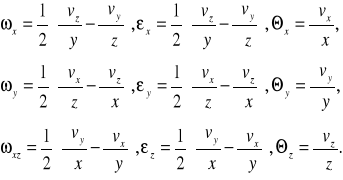
(2)

Otrzymane powyżej wyrażenia na v_x1, v_y1 i v_z1 można wówczas napisać w postaci:

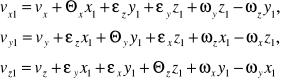
(3)

Wprowadźmy następującą pomocniczą funkcję:

(4)

Której pochodne względem współrzędnych x₁, y₁, z₁ mają postać

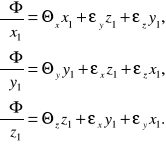
(5)

Za pomocą funkcji Φ możemy napisać wzory na rzuty prędkości w następującej skróconej postaci:

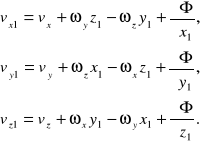
(6)

Wyjaśnijmy fizyczny sens równań (6).

Wyrazy v_x, v_y i v_z są oczywiście rzutami prędkości przesuwania się w prze­strzeni rozpatrywanej cząstki jako ciała sztywnego.

Wykorzystajmy rozwiązanie zadania z mechaniki teoretycznej o obrocie ciała sztywnego do koła nieruchomej osi i zauważmy, że różnice

ω_yz₁-ω_zy₁, ω_zx₁-ω_xz₁, ω_xy₁-ω_yx₁ wyrażają rzuty prędkości kątowej elementu płynu (oraz ciała sztywnego) dookoła chwilowej osi, przechodzącej przez punkt M. Taki ruch obrotowy elementu płynu nazywany jest ruchem wirowym, a składowe prędkości kątowej ω_x, ω_y, ω_z - składowymi wiru.

Jak wynika z równań (2)

(2')

Wyjaśnimy z kolei sens składników

Z rozważań fizycznych widać wyraźnie przede wszystkim to że element płynu, na skutek różnicy prędkości w różnych jego punktach, będzie ulegać deformacji. Wynika stąd bezpośrednio, że wyrażenia

stanowią składowe prędkości deformacji elementu. Udowodnimy to na prostym przykładzie.

Niech nieskończenie mały element pły­nu ma w chwili t kształt prostokątnego równoległościanu. Dla uproszczenia roz­patrzymy rzuty tego elementu na płaszczyznę x, y, to znaczy nieskończenie mały prostokąt MBDC (rys.2)

Rys2

Jeżeli składowe prędkości punktu M(x,y) prostokąta oznaczymy przez v_x i v_y, wówczas może­my napisać składowe prędkości w punktach C(x+x₁,y) oraz B(x, y+y₁) z dokładnością do małych pierwszego rzędu w postaci:

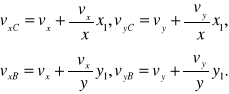
(7)

Ponieważ interesuje nas względne przesunięcie punktów C i B (względem punktu M), przepiszemy równania (7) w następujący sposób:

Jak widzimy, prędkości

oraz

są prędkościami liniowej deformacji boków prostokąta MDBC. Natomiast prędkości

oraz

wskazują na obrót boków MC i MB (rys. 2), są zatem prędkościami

deformacji postaciowej prostokąta MBDC przekształcającymi go w pewien równoległobok (linia kreskowana na rys. 2). Widzimy, że bok MC obraca się z prędkością kątową

bok zaś MB - z prędkością kątową

Ponieważ prędkość zmiany kąta prostego MBC składa się z prędkości kątowych obrotu boków MC i MB, stanowi ona zatem sumę

Rozważając w sposób analogiczny inne boki równoległościanu (albo ich rzuty na płaszczyzny współrzędnych), można równie prosto dowieść, że wielkość

stanowi prędkość deformacji liniowej wzdłuż osi z oraz że wielkości prędkości kątowych odkształcenia postaciowego pozostałych kątów prostych równoległościanu są wyrażone przez zależności

i

Z powyższego wynika, że wielkości

są istotnie składowymi prędkości deformacji elementu płynu, przy czym wielkości εx,εy i εz określają odkształcenia postaciowe, zaś wielkości Θx Θy , i Θz - deformację liniową (rozciąganie lub ściskanie).

Powracając do równań (6), których sens fizyczny został całkowicie wyjaśniony, dochodzimy do następującego ważnego wniosku :

Elementarny ruch elementu płynu składa się z ruchu postępowego jego środka z prędkością

obrotu z prędkością kątową

dookoła pewnej osi przechodzącej przez ten środek oraz ruchu reformacyjnego określonego funkcją

Niech nieskończenie mały element płynu ma w pewnej chwili t kształt kuli, której środek leży w punkcie O(x, y, z,) i której promień równa się a (rys 3).

Rys. 3

Obierzemy ruchome osie współrzędnych x₁, y₁, z₁ (równoległe do nieruchomych osi x, y, z) w ten sposób, aby początek układu znajdował się w środku kuli, oraz aby układ przesuwał się ruchem postępowym wraz ze środkiem kulistego elementu płynu. Niech składowe prędkości środka O elementu będą v_x0, v_y0, v_z0.

Na podstawie powyższego możemy wówczas podać składowe prędkości dowolnego punktu N(x₁, y₁, z₁) na powierzchni elementu w następującej postaci:

Łatwo przekonać się, że funkcja , będąc jednorodnym wielomianem drugiego stopnia względem współrzędnych x₁, y₁, z₁, stanowi powierzchnię drugiego stopnia mającą środek symetrii leżący w początku układu współrzędnych - jest to elipsoida, zwana elipsoidą deformacji.

Jeżeli osie współrzędnych x₁, y₁, z₁, skierujemy wzdłuż osi elipsoidy deformacji wówczas - jak wiadomo - znikną wyrazy zawierające iloczyny współrzędnych różnorodnych. Osie elipsoidy deformacji nazywamy głównymi osiami deformacji.

Przy takim wyborze osi będziemy mieli :

a zatem

co oznacza, że wzdłuż głównych osi deformacji zachodzą jedynie deformacje liniowe.

Rozpatrywany przez nas element płynu ma w chwili początkowej (przed deformacją) kształt kulki. Napiszemy równanie tej kulki w postaci

Oznaczmy przez x₂,y₂,z₂ współrzędne (względem środka O), jakie będzie miał punkt N elementu po upływie nieskończenie małego odcinka czasu dt. Ograniczając się do rozpatrzenia jedynie ruchu reformacyjnego, możemy wówczas na podstawie wzoru (9) napisać :

gdyż

są prędkościami deformacji.

Stąd:

Podstawiając wartości x₁,y₁,z₁, do równania kuli, otrzymamy

Równanie (10) jest równaniem elipsoidy z półosiami:

Zatem nieskończenie mała kula deformując się zmienia się w nieskończenie małą elipsoidę, której osie skierowane są wzdłuż głównych osi deformacji (rys3).

Znajdźmy teraz zmianę objętości rozpatrywanego, nieskończenie małego elementu.

W tym celu musimy od objętości elipsoidy odjąć objętość kulki:

gdzie

• współczynnik rozszerzalności objętościowej.

Jeżeli płyn jest nieściśliwy, wtedy współczynnik rozszerzalności objętościowej Θ=0, otrzymamy więc znane równanie ciągłości dla płynu nieściśliwego

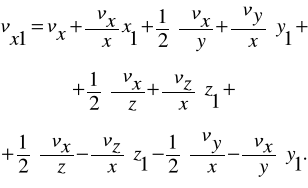
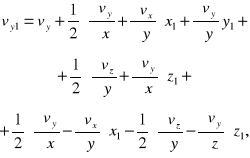
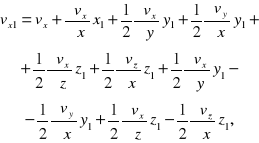
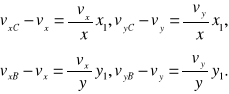
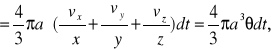
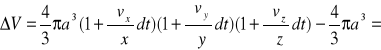
(10)

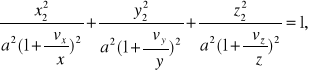
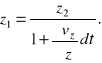
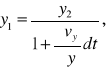
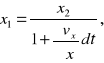
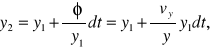
(9)

---