9. Funkcje potęgowe i pierwiastkowe

Funkcją pierwiastkową nazywamy funkcję postaci
gdzie
N i
Dziedzina tej funkcji zależy od wartości n. Jeżeli n jest liczbą parzystą, to dziedziną jest zbiór
dla n nieparzystych funkcja określona jest dla wszystkich liczb rzeczywistych.

Funkcją potęgową nazywamy funkcję postaci
gdzie
R. Dziedzina tej funkcji zależy od wartości
Jeżeli
jest liczbą naturalną dodatnią, to
R; w przypadku gdy
jest liczbą całkowitą niedodatnią, to otrzymujemy funkcję wymierną określoną dla
Gdy
jest liczbą niecałkowitą (ułamkową lub niewymierną), to dziedziną funkcji jest przedział
W szcze­gólnych przypadkach funkcja potęgowa jest obcięciem funkcji pierwiastkowej do przedziału

Przykłady. Rozwiążemy równania pierwiastkowe.

a)

.

Rozwiązanie. Możemy zastosować dwie metody.

Metoda analizy starożytnych

Przypuśćmy, że x jest rozwiązaniem nierówności
Wówczas

Ponieważ w pierwszym kroku rozwiązania wystąpiła implikacja, więc istnieje możliwość pojawienia się tzw. pierwiastków obcych. Dlatego konieczne jest wykonanie sprawdzenia, czy rzeczywiście znalezione liczby są faktycznie rozwiązaniami równania
Niech symbol
oznacza wartość lewej strony
w punkcie x oraz P - jej prawą stronę. Mamy

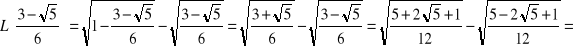
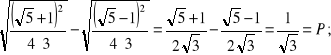
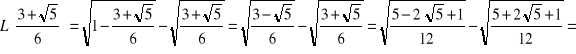
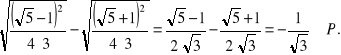
Zatem tylko liczba
jest rozwiązaniem równania
Zauważmy, że pierwiastek obcy
należy do dziedziny równania.

Metoda równań równoważnych

Zaczynamy od zastrzeżeń:

Istota metody polega na utworzeniu ciągu równań równoważnych. Będziemy zmuszeni podnosić obie strony danego równania do kwadratu i tu trzeba zadbać o to, aby obie jego strony były wyrażeniami tego samego znaku (wtedy funkcja
obcięta do przedziału
lub
jest różno­wartościowa). Mamy

Ponieważ lewa strona ostatniego równania jest wyrażeniem nieujemnym, więc przed podniesieniem obu jego stron do kwadratu, musimy zastrzec, że

Pod takim warunkiem możemy kontynuować kroki równoważne:

gdyż
Rozwiązaniem równania
jest więc liczba

Zaletą przedstawionego rozwiązania jest brak konieczności wykonania kłopotliwego sprawdzenia, z drugiej strony trzeba było zrobić na początku zastrzeżenia.

b)

.

Rozwiązanie. Jest oczywiste, że musi być
i wtedy

Podstawiamy
:

Dalsze postępowanie „rozbijemy” na przypadki.

1⁰
Wtedy

Znaleziona wartość nie należy do rozpatrywanego przedziału.

2⁰
Wtedy

Rozwiązaniami są więc wszystkie liczby należące do przedziału

3⁰

Znaleziona wartość należy do rozpatrywanego przedziału.

Reasumując, zbiorem rozwiązań rozważanego równania z niewiadomą t jest przedział
Wracając do niewiadomej x otrzymujemy ciąg równoważnych nierówności

.

Zbiorem rozwiązań nierówności (*) jest przedział

c)

Rozwiązanie. Zastrzeżenie:
.

Przez podstawienie
sprowadzimy równanie do równania kwadratowego:

Równanie
jest sprzeczne. Dla drugiej znalezionej wartości t mamy:

Liczba
spełnia zastrzeżenie i dlatego jest ona rozwiązaniem naszego równania.

Przykłady. Rozwiążemy wybrane nierówności.

a)

Rozwiązanie. Zauważmy na wstępie, że w przypadku nierówności pierwiastkowych raczej się nie stosuje metody analizy starożytnych ze względu na trudność z eliminacją rozwiązań obcych (znaleziony zbiór „kandydatów” na rozwiązania byłby na ogół nieskończony).

Dziedziną rozważanej nierówności jest zbiór
Rozpatrzmy trzy przypadki.

1⁰
Wtedy lewa strona nierówności jest ujemna, a prawa nieujemna. Nierówność jest więc prawdziwa dla każdego

2⁰
Teraz obie strony nierówności są ujemne. Korzystają z faktu, że funkcja
obcięta do przedziału
jest malejąca, otrzymujemy równoważności:

3⁰
W tym przypadku nierówność jest sprzeczna, gdyż jej lewa strona jest nieujemna, a prawa ujemna.

Ostatecznie zbiorem rozwiązań badanej nierówności jest przedział

b)

Rozwiązanie. Musi być spełnione zastrzeżenie:
lub
Ponadto, ponieważ lewa strona nierówności jest zawsze nieujemna, więc rozwiązań musimy poszukać wśród liczb spełniających nierówność
W konsekwencji musimy założyć, że
Wtedy

Uwzględniając założenie, widzimy, że nierówność jest prawdziwa dla

c)

Rozwiązanie. Podobnie, jak w poprzednim rozwiązaniu, muszą być spełnione zastrzeżenie:

Dla
prawa strona nierówności jest ujemna, a lewa nieujemna, więc nierówność jest prawdziwa.

Dla
obie strony nierówności są nieujemne, więc możemy ją podnieść stronami do kwadratu, otrzymując:

W konsekwencji w przedziale
nie ma rozwiązań. Analizowana nierówności zachodzi tylko dla

Rozdział 9. Funkcje potęgowe i pierwiastkowe 71

69

x

y

x

y

---