Rys.4.36b
…………………………………………………………………………………………………..
Rys.4.55
………………………………………………………………………………………………….
Od współczynnika mocy zależy również przebieg zmienności chwilowej wartości mocy czynnej ![]()
. Niżej zostaną rozpatrzone cztery przypadki obwodów:
- obwody zawierające tylko rezystancję,
- obwody zawierające tylko indukcyjność,
- obwody zawierające tylko pojemność,
- obwody zawierające rezystancję i indukcyjność.
Obwody z innymi kombinacjami elementów można rozpatrywać analogicznie.
Przypadek I
Obwód zawiera tylko rezystancję, czyli prąd jest w fazie z napięciem (![]()
). Przebiegi czasowe napięcia, prądu i mocy czynnej przedstawiono na rys.4.41.
Uwaga: Tekst pisany czerwoną czcionką służy tylko do umiejscowienia tekstu do podmiany (czarna czcionka).
.....................................................................................................................................................................................
![]()
![]()
Po scałkowaniu otrzymuje się - w wzorze powyżej brakuje „dt”
(4.128)
……………………………………………………………………………………………..........
![]()
(4.143)
W wzorze powyżej jest mała litera „i”.
…………………………………………………………………………………………………..
Dodać rozdział
4.12. Liczby zespolone i ich zastosowanie w elektrotechnice
4.12.1. Liczby zespolone
Liczbą zespoloną z nazywa się w matematyce parę uporządkowanych liczb (a,b), zapisywaną jako
![]()
(4.213)
przy czym a jest częścią rzeczywistą tej liczby![]()
, a b częścią urojoną ![]()
. Symbol ![]()
nazywa się jednostką urojoną (![]()
![]()
,![]()
).
W elektrotechnice jednostkę urojoną oznacza się symbolem j, bowiem symbolem i przyjęto oznaczać wartości chwilowe prądu zmiennego.
Wyrażenie (4.213) nazywa się postacią algebraiczną liczby zespolonej. Oprócz takiej postaci istnieją również inne, a mianowicie wykładnicza
![]()
(4.214)
i trygonometryczna
![]()
) (4.215)
przy czym
![]()
(2.216)
nazywa się modułem liczby zespolonej, a
![]()
(4.217)
argumentem liczby zespolonej.
Przejście od postaci wykładniczej do postaci trygonometrycznej lub odwrotnie umożliwia wzór E u l e r a
![]()
(4.218)
Liczbą ![]()
, sprzężoną z liczbą zespoloną ![]()
, nazywa się się liczbę zespoloną
![]()
(4.219)
Ponieważ argumenty liczb zespolonych nie są jednoznacznie określone (mogą się różnić się o dowolną krotność ![]()
), to w elektrotechnice rozpatruje się tylko wartości argumentów z przedziału (![]()
).
Podstawowe działania na liczbach zespolonych w postaci algebraicznej:
dodawanie
![]()
odejmowanie
![]()
mnożenie
![]()
dzielenie
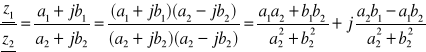
podnoszenie do potęgi
![]()
porównywanie dwóch liczb zespolonych
![]()
4.12.2. Przedstawianie wielkości sinusoidalnie zmiennych za pomocą liczb zespolonych
W elektrotechnice wielkości zespolone oznacza się przez podkreślenie dużej litery, oznaczającej daną wielkość, np. ![]()
, ![]()
, ![]()
itp.
Rozpatrzmy dowolną liczbę zespoloną
![]()
(4.220)
w której ![]()
jest modułem liczby ![]()
, a dolny indeks t oznacza, że wielkość oznaczona tym symbolem jest funkcją czasu.
Jeżeli zapisać tę liczbę w postaci trygonometrycznej, tj.
![]()
(4.221)
to z takiego zapisu wynika, że zarówno część rzeczywista, jak i urojona, zmieniają się w czasie w sposób sinusoidalny, przy czym ![]()
można traktować jako amplitudę oznaczonej tym symbolem wielkości, a ![]()
jako jej fazę. Dalsze rozważania zostaną przedstawione na przykładzie napięcia i prądu, ale będą dotyczyły wszystkich wielkości sinusoidalnie zmiennych, stosowanych w elektrotechnice.
Wartości chwilowe napięcia i prądu są opisane poznanymi już wcześniej zależnościami, a mianowicie
![]()
![]()
W postaci zespolonej można je przedstawić w sposób następujący:
![]()
(4.222a)
![]()
(4.222b)
Wartości chwilowe u napięcia i prądu i można otrzymać z wyrażeń (4.222a,b) poprzez wyodrębnienie z nich części urojonej, czyli
![]()
(4.223a)
![]()
(4.223b)
Na podstawie powyższych rozważań można zdefiniować wartości zespolone napięcia i prądu jako:
|
(4.224a) |
|
(4.224a) |
przy czym m o d u ł y wartości zespolonych równają się w a r t o ś c i o m s k u t e c z n y m wielkości sinusoidalnych, a a r g u m e n t y - f a z o m tych wielkości.
Związki między wartościami zespolonymi i wielkościami ![]()
i ![]()
określają zależności
|
(4.225a) |
|
(4.225b) |
Wyznaczanie wartości chwilowych napięcia u oraz prądu i na podstawie znajomości ich wartości zespolonych ![]()
oraz ![]()
polega na wyodrębnieniu części urojonych wyrażeń ![]()
oraz ![]()
, czyli
|
(4.226a) |
|
(4.226b) |
Metoda obliczania obwodów prądu sinusoidalnie zmiennego, sprowadzająca się do działań na liczbach zespolonych, nazywa się metodą liczb zespolonych lub metodą symboliczną.
Przykład 4.25
Wyznaczyć wartości zespolone prądu ![]()
oraz napięcia ![]()
.
Rozwiązanie
Z (4.226) wynika, że wartość zespolona prądu wyniesie
![]()
a wartość zespolona napięcia ![]()
Przykład 4.26
Obliczyć wartości chwilowe napięcia i prądu danych w postaci zespolonej
![]()
![]()
Rozwiązanie
W tym celu należy przedstawić dane wielkości zespolone w postaci wykładniczej i wyodrębnić z otrzymanych wyrażeń części urojone.
Moduły napięcia i prądu są równe
![]()
![]()
a ich kąty fazowe
![]()
![]()
Postać wykładniczą wartości zespolonych napięcia i prądu można zapisać jako
![]()
![]()
a ich wartości chwilowe, zgodnie z (4.226), w postaci wyrażeń
![]()
V
![]()
A
4.12.3. Związek liczb zespolonych z wskazami (wektorami) wirującymi
Niech będzie dana liczba zespolona ![]()
. Obrazem geometrycznym tej liczby na płaszczyźnie zmiennej zespolonej jest wektor ![]()
, łączący początek układu współrzędnych z punktem A, o współrzędnych (a, b), przy czym odcięta a jest równa składowej rzeczywistej liczby zespolonej ![]()
, a rzędna składowej urojonej b tej liczby (patrz rys.4.66). Długość wektora ![]()
jest równa modułowi liczby ![]()
, a kąt, jaki tworzy ten wektor z dodatnią półosią liczb rzeczywistych, jest równy jej argumentowi ![]()
Moduł liczby
![]()
(4.227)
jest równy ![]()
, a argument ![]()
, czyli jest liniową funkcją czasu.
Rys.4.66. Odwzorowanie geometryczne liczby zespolonej
Obrazem geometycznym rozpatrywanej liczby ![]()
(4.227) na płaszczyźnie zmiennej zespolonej jest więc wektor ![]()
, wirujący ze stałą prędkością kątową ![]()
w kierunku dodatnich kątów. Początek tego wektora jest nieruchomy i znajduje się w początku układu współrzędnych O. Jak wiadomo z wcześniejszych rozważań, takie wektory nazywają się wektorami lub wskazami wirującymi. W elektrotechnice wielkości zespolone typu ![]()
będą najczęściej nazywane wskazami wirującymi.
Rzut wskazu wirującego ![]()
na oś urojoną jest równy części urojonej wyrażenia (4.227), czyli ![]()
.
Oś, na którą rzutuje się wskaz, nazywa się osią czasu. W tym przypadku jest nią nieruchoma oś urojona „Im” układu współrzędnych. Ponieważ rzut wskazu ![]()
zmienia się sinusoidalnie w czasie, więc wskaz wirujący ![]()
wraz z nieruchomą osią czasu odwzorowuje wielkość sinusoidalną.
4.12.4. Zastosowanie liczb zespolonych do obliczania obwodów elektrycznych prądu sinusoidalnego
Można wykazać, że poznane dotyczczas prawa, dotyczące obwodów elektrycznych prądu sinusoidalnego (prawo Ohma i prawa Kirchhoffa), obowiązują również dla obwodów opisanych za pomocą liczb zespolonych. Równania, opisujące obwody elektryczne prądu sinusoidalnego w formie zespolonej, można otrzymać bezpośrednio z równań zapisanych dla wartości chwilowych. W tym celu należy:
wartości chwilowe napięć, prądów i sił elektromotorycznych zastąpić ich wartościami zespolonymi, np. ![]()
, ![]()
, ![]()
itp.,
operator różniczkowania ![]()
zastąpić przez ![]()
, tj. ![]()
,
operator całkowania ![]()
zastąpić przez ![]()
, tj. ![]()
.
Jeżeli, na przykład, obwód złożony z szeregowo połączonych elementów R i L zasilany ze źródła sinusoidalnej siły elektromotorycznej e, jest opisany równaniem dla wartości chwilowych w postaci
![]()
(4.228)
to odpowiadające temu obwodowi równanie, zapisane za pomocą liczb zespolonych, ma postać
![]()
(4.229)
Analogicznie, dla obwodu złożonego z szeregowo połączonych elementów R i C, zasilanego ze źródła sinusoidalnej siły elektromotorycznej e, równaniu dla wartości chwilowych
![]()
(4.230)
będzie odpowiadało równanie w postaci zespolonej
![]()
(4.231)
Do obliczania obwodów elektrycznych prądu sinusoidalnego z wykorzystaniem liczb zespolonych, konieczne jest jeszcze wprowadzenie pojęcia impedancji zespolonej ![]()
. Otóż impedancją zespoloną (opornością zespoloną lub opornością symboliczną) dwójnika, nazywa się iloraz wartości zespolonych napięcia i prądu, tj.
![]()
(4.232)
Jeżeli napięcie ![]()
, a prąd ![]()
to
![]()
(4.233)
czyli iloraz wartości skutecznych napięcia i prądu
![]()
(4.234)
jest modułem![]()
impedancji ![]()
, a jej argumentem jest kąt przesunięcia fazowego ![]()
(arg![]()
).
Impedancję zespoloną można przedstawić w postaci wykładniczej
![]()
(4.235)
lub algebraicznej
![]()
(4,236)
przy czym rezystancja jest częścią rzeczywistą impedancji zespolonej, a reaktancja częścią urojoną. Moduł impedancji wyraża się więc zależnością
![]()
(4.237)
a argument zależnością
![]()
(4.238)
Korzystając z wzoru Eulera
![]()
otrzymuje się jeszcze inne związki między częściami składowymi impedancji, a mianowicie
![]()
oraz ![]()
(4.239)
Przykład 4.27
Dwójnik, zawierający szeregowo połączone elementy R i L, jest zasilany napięciem sinusoidalnym o wartości ![]()
V i częstotliwości![]()
. Prąd płynący przez dwójnik wynosi ![]()
. Obliczyć rezystancję R, reaktancję indukcyjną ![]()
oraz indukcyjność L.
Rozwiązanie
Aby obliczyć rezystancję i reaktancję trzeba najpierw obliczyć z definicji impedancję zespoloną dwójnika
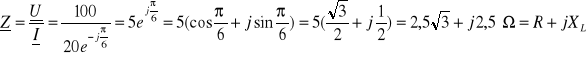
Ponieważ dwie liczby zespolone są równe wtedy, gdy ich części rzeczywiste i urojone są odpowiednio sobie równe, to rezystancja ![]()
, a reaktancja indukcyjna ![]()
. Uwzględniając, że ![]()
otrzymuje się, że
![]()
Przykład 4.28
W obwodzie jak na rys.4.67 napięcie ![]()
, rezystancja ![]()
, reaktancja indukcyjna ![]()
a reaktancja pojemnościowa ![]()
. Obliczyć wartość skuteczną prądu pobieranego ze źródła.
Rys.4.67. Schemat obwodu do przykładu 4.28
Rozwiązanie
Aby obliczyć wartość skuteczną prądu pobieranego ze źródła, trzeba najpierw obliczyć jego wartość zespoloną. W tym celu należy obliczyć impedancję zespoloną całego obwodu. Impedancja ta składa się z rezystancji R i reaktancji pojemnościowej ![]()
połączonych równolegle, oraz szeregowo do nich dołączonej reaktancji indukcyjnej ![]()
.
Impedancja zespolona całego obwodu wyniesie, więc
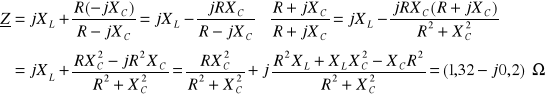
prąd pobierany ze źródła w postaci zespolonej
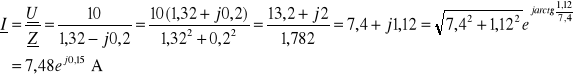
a jego wartość skuteczna ![]()
.