2. REGULATOR SAMONASTRAJAJĄCY STR

Zaprojektowanie regulatora samonastrajającego STR (Self Tuning Regulator) można sprowadzić do następujących kroków:

1. Znajdowanie parametrów dla systemu ze sprzężeniem zwrotnym,

2. Wyznaczanie modelu kontrolowanego procesu,

3. Decyzje dotyczące metody projektu,

4. Obliczanie parametrów algorytmu.

Parametry systemu ze sprzężeniem zwrotnym zależą między innymi od jakości wymuszeń kontrolowanej zmiennej, dostępna wielkości (siły) kontrolowanego sygnału oraz nieliniowości systemu poddanego kontroli. To stanowi o tym, że parametry są determinowane przez proces inżynierski na starcie procedury projektu regulatora. Regulatory STR opierają się na metodzie wyliczania nieznanych parametrów procesu. Wyliczane parametry zazwyczaj prowadzą w sposób naturalny do wyboru metody projektowej. Na przykład główny parametr ma za zadanie utrzymać stały proces wyjściowy i jeżeli zakłócenia są z rzadka wielkimi zakłóceniami, procedura projektowa może być metodą która tak szybko jak to możliwe eliminuje wpływ zakłóceń. Wybór parametrów i metod projektowych jest zazwyczaj dokonywany przez projektanta pętli kontroli. W regulatorach samonastrajających, wyznaczanie modelu kontrolowanego procesu oraz obliczanie parametrów w kontrolerze są wykonywane automatycznie.

Na schemacie blokowym - rys. 2.1 przedstawiona jest struktura kontrolera samonastrajającego.

Rys.2.1.Schemat blokowy regulatora samonastrajającego (STR)

STR składa się z dwóch zamkniętych pętli. Pierwsza pętla jest konwencjonalną pętlą zwrotną kontrolera składającą się z procesu i kontrolera. W układzie tym wyjście procesu jest mierzone i porównywane z sygnałem odniesienia. Różnica pomiędzy sygnałem odniesienia i sygnałami wyjściowymi jest używana do obliczania sygnału kontroli wysyłanego do procesu.

Kontroler posiada parametry, które determinują jego właściwości. Te parametry są określane przez drugą pętlę regulatora samonastrajającego - pętlę uaktualniającą (ang. updating loop) [17].

Na rysunku 2.1. pętla uaktualniania składa się z dwóch głównych bloków. Pierwszy blok jest blokiem obliczeń, który funkcjonuje w oparciu o dane wejścia i wyjścia procesu określając jego model matematyczny. Drugim blokiem jest blok „projektu kontrolera”. Ten blok używa matematycznego modelu procesu i obliczeń zewnętrznych do określenia parametrów kontrolera, które następnie są wysyłane do kontrolera. W takiej konfiguracji STR jest zazwyczaj nazywany pośrednim regulatorem samonastrajającym. Koniecznym jest, ażeby pętla zwrotna kontrolera była zamknięta cały czas w celu zajęcia się wpływem zakłóceń i zmian w sygnale celu regulacji. Pętla uaktualniająca parametrów kontrolera może być odłączona tak szybko, kiedy obliczone parametry osiągną swoje końcowe wartości, to znaczy kiedy kontroler nastroi albo przystosuje się do wyliczeń zewnętrznych i procesu. W przypadku, jeżeli proces zmienia się cały czas jest konieczne ciągłe aktualizowanie modelu procesu oraz parametrów kontrolera. W wyniku ciągłej aktualizacji powstaje tzw. regulator adaptacyjny.

Powyższe rozważania implikują, iż regulator samonastrajający jest kontrolerem adaptacyjnym, jeżeli aktualizacja parametrów jest ciągła. Regulatory adaptacyjne są zatem specjalną klasą regulatorów samonastrajających. Jedną z pierwszych osób opisujących idee wykorzystania regulatorów STR w drógiej połowie lat pięćdziesiątych dwudziestego wieku jest Kalman [18], który opisuje aktualizację używającą parametru obliczanego i projektu. Termin regulatora samonastrajającego STR powstał za sprawą naukowców Astroma i Wittenmarka [1], którzy wykonali pierwsze analizy właściwości stacjonarnych regulatorów samonastrajających, bazujących na kontroli minimalnowariancyjnej. Stabilność systemu z zamkniętą pętlą i zbieżność właściwości szerzej zostały przeanalizowane przez Goodwina, Ramadgea i Cainesa [19] na początku lat osiemdziesiątych. Więcej szczegółów właściwości STR i kontrolerów adaptacyjnych możemy znaleźć w Astromie i Wittenmarku [1].

Możliwe jest wykonanie reparametryzacji procesu i kontrolera takich, że parametry kontrolera mogą być wyliczane bezpośrednio. To prowadzi do bezpośredniej regulacji samonastrajającej.

1. Zastosowanie regulatorów samonastrajających

Obliczenia w regulatorze samonastrajającym są w miarę proste, ale zawierają operacje nieliniowe i logiczne. To implikuje, że regulatory samonastrajające są projektowane oraz realizowane przy użyciu komputera. Algorytm może być blokiem w pakiecie programowym, który jest używany dla większego procesu kontroli aplikacji. STR może być również wdrożony do określonych urządzeń na kilku pętlach kontroli.

Kontrola samonastrajająca od połowy lat siedemdziesiątych była używana w wielu „aplikacjach”, głównie sterujących procesami przemysłowymi. Kontrola samonastrajająca znalazła zastosowanie w procesie wytwarzania papieru, reakcjach chemicznych, autopilotach i maszynach wykonujących dializę.

Regulatory samonastrajające i kontrolery adaptacyjne w ogólności znajdują zastosowanie w trzech kategoriach zastosowań:

1. kiedy proces posiada długie czasy opóźnień,

2. kiedy możliwe jest użycie jednokierunkowości,

3. kiedy zakłócenia wpływające na proces mają różne charakterystyki czasowe.

Głównym powodem dlaczego STR (regulacja adaptacyjna) doskonale sprawdzają się tych sytuacjach, jest lepsza możliwość dobrej regulacji tego typu procesów, aniżeli za pomocą innych rozwiązań. W wyniku tego jest możliwe otrzymanie dokładnych modelów kontrolowanych procesów oraz zakłóceń.

1. Identyfikacja procesu w systemie regulacji adaptacyjnej

Identyfikacją nazywamy takie wyznaczenie modelu opisującego dynamikę obiektu sterowania, aby błąd pomiędzy obiektem a jego modelem był minimalny.

Układy sterowania adaptacyjnego powinny pracować przy zmieniających się parametrach obiektu i w obecności zakłóceń, których wpływ kompensowany jest przez sterowanie [11].

Istnieje wiele algorytmów estymacji, które mogą być wykorzystane do strojenia. Układy powinny być zaprojektowane w taki sposób, aby mogły pracować w odpowiednich warunkach zdefiniowanych przez przebieg zakłóceń, zamianę parametrów wartość zadaną regulatora. Chociaż istnieje wiele pozycji literatury poświęconych tym zagadnieniom to jednak wyniki teoretyczne dotyczące stabilności, optymalności, rzędu modelu, zmianie parametrów i zgodności ocen są ważne tylko dla pewnych wyidealizowanych warunków. Przeważnie czyni się założenia o stałości parametrów w standardowych metodach estymacji rekurencyjnej bez zapominania danych, oraz zerowej wartości zadanej regulatora. W praktyce parametry zmieniają się, w estymacji używa się współczynnika zapominania λ[11].

W powszechnie rozważanym podejściu do oceny parametrów stosuje się bieżące pomiary wejścia i wyjścia obiektu w odpowiednim algorytmie estymacji. Jednym z najczęściej stosowanych metod estymacji parametrów obiektu jest algorytm Rekurencyjny Rozszerzonej Metody Najmniejszych Kwadratów (RELS-Recursive Extended Least Squares) w wersji ważonej, w której wykorzystuje się współczynnik zapominania λ [11]. Współczynnik ten umożliwia uwzględnianie aktualnych pomiarów i zapominanie starych.

W sterowaniu adaptacyjnym ważne jest, by oceniać parametry procesu na bieżąco. Dla adaptacyjnego systemu sterowania przystosowujący się mechanizm jest oparty głównie na identyfikowaniu systemu. Strojenie się regulatora (rys.2.1) wyraźnie zawiera powtarzający się estymator parametru. Mówiąc wprost, estymacja parametrów procesu jest częścią identyfikacji systemu. W ogólniejszym sensie, identyfikacja systemu jest operacją wyboru struktury modelu, projektowania eksperymentu, estymacji parametru i kontroli danych.

Poniżej opisano bardziej szczegółowo, jak są skonstruowane regulatory samonastrajające. Zostaną ukazane główne właściwości STR. Na potrzeby opisu zostaną wyszczególnione modele procesu, parametry, algorytm, moduł obliczający i wybrane metody projektu. Dla opisu procesu użyto modeli dyskretnych. Większość implementacji STR wykonuje komputer.

1. Modele procesu

Ogólnie proces modelowania polega na ustalaniu powiązań (relacji) między zmiennymi opisującymi proces. Zmiennymi tymi są:

• zmienne sterujące u (sterowanie),

• zmienne wewnętrzne x (stan),

• zmienne wyjściowe y (wyjście),

• zmienne parametryczne α,β (parametry modelu),

• zmienne zakłócające e (zakłócenia).

Proces jest opisany za pomocą próbkowania danych systemu liniowego. Proces przyjmuje także postać: jedno wejście i jedno wyjście. Model jest dany jako równanie różnicowe - w najprostszej postaci bez zakłóceń jako:

(2.1)

gdzie:

y(k) - wyjściowy sygnał przy chwilowym próbkowaniu k

u(k) - sygnał sterujący

d - czas opóźnienia systemu

Założono, że czas jest skalowany tak, że okres próbkowania zawiera się w jednej jednostce czasu. Równanie 2.1 jest ogólnym opisem liniowego systemu z próbkowaniem danych. Dla uzyskania niewielkiego rozmiaru opisu systemu można wprowadzić operator przesunięcia w tył q^-1. Operator ten jest definiowany w następujący sposób:

(2.2)

Operowanie na sekwencji czasu zmienia argument czasu o jeden krok w tył.

Używając operatora opóźnienia i wielomianów:

(2.3)

system może być zapisany jako:

(2.4)

gdzie
jest nazywane funkcją impulsywnego przeniesienia (ang. Pulse-transfer function) lub transmitancją impulsową toru sterowania [1], [7].

Opisane wyżej równania są uproszczone. Poniżej przedstawiono ogólny schemat blokowy modelu procesu oraz opisano krótko rodzaje modeli.

Rys 2.2. Schemat blokowy modelu procesu

Na powyższym rysunku:

u(k) - sygnał sterujący

y(k) - sygnał wyjściowy

e(k) - ciąg niezależnych i jednakowo rozłożonych zmiennych losowych o zerowej wartości średniej i wariancji σ²(e) (biały szum)

- pewne transmitancje

q^-1 - operator przesunięcia wstecz o pojedynczą próbkę

Ogólna struktura modelu dana jest równaniem:

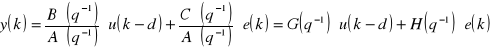
(2.5)

gdzie
- transmitancja toru sterowania

- transmitancja toru zakłócenia

Inną postać struktury modelu przedstawiono zależnością 2.6.

(2.6)

gdzie d - to czas opóźnienia

Wielomiany natomiast są przyjęte w postaci:

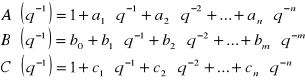
(2.7)

Wielomiany
oraz
nazywane są monicznymi, ponieważ A(0)=1 oraz C(0)=1

Opis procesu w postaci równania 2.6. można przedstawiać w postaciach szczególnych, co prowadzi do wyróżnienia następujących modeli [6]:

1. autoregresji (AR)

(2.8)

2. ruchomej średniej (MA)

(2.9)

3. autoregresji z ruchomą średnią (ARMA)

(2.10)

4. skończonej odpowiedzi impulsowej (FIR)

(2.11)

5. autoregresji z wejściem zewnętrznym (ARX)

(2.12)

6. autoregresji z ruchomą średnią z sygnałem zewnętrznym (ARMAX)

(2.13)

1. Algorytmy estymacji parametrów

Obliczanie modelu procesu może być wykonane na wiele sposobów. Jako podstawową omówiono rekursywną metodę najmniejszych kwadratów (RLS). Zdefiniujmy wektory:

(2.14)

Wektor parametrów
zawiera nieznane parametry procesu, dopóki wektor
zawiera stare wejścia i wyjścia procesu i jest zwany wektorem znanych zmiennych regresyjnych, będących opóźnionymi próbkami wielkości sterującej i wyjściowej obiektu. Argument (k-1) wektora φ wyjaśnia, iż najmłodsza zmienna regresyjna w nim zawarta pochodzi z chwili (k-1) . Model procesu może być zapisany jako:

(2.15)

Metoda najmniejszych kwadratów ustanowiona przez Gaussa [20], mówi, że obliczenie
powinno być wybrane jako
, ze minimalizowaną funkcją strat

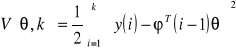
(2.16)

Podanie początkowych wartości parametrów
i niewiadomych parametru estymacji P(0) umożliwia otrzymanie rekursywnego rozwiązania problemu najmniejszych kwadratów. Obliczony parametr może być uaktualniony rekursywnie używając:

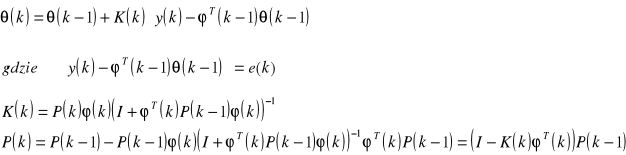
e(k) - błąd identyfikacji,

K(k )- wektor korekcyjny,

P(k) - macierz kowariancji,

θ(k) - estymator wektora θ.

Ponieważ algorytm najmniejszych kwadratów jest rekursywny obliczanie z czasem k jest uzyskiwane jako aktualizacja obliczenia z czasem k-1. Korekcja warunku zależy od ostatniego procesu wyjściowego, który jest porównywany z predykcyjnym (przewidującym) wyjściem bazującym na parametrze obliczonym z czasem k-1. Macierz P(k) może być interpretowana jako obliczenie niewiadomej parametru obliczonego z czasem k. Statystyczna interpretacja może być zrobiona rygorystyczną przez zrobienie założenia zakłócenia, które wpływa na system.

Rekursywna metoda najmniejszych kwadratów jest dobrze dopasowana do parametru procesu obliczeń kiedy nie ma zakłóceń albo kiedy proces białego szumu jest dodany do właściwej strony równania (2.4). Dla innego szumu albo zakłócenia możliwe jest użycie innego wariantu rekursywnej metody najmniejszych kwadratów.

Odkąd formuły aktualizujące (2.17) są rekursywne mogą być użyte także do ciągłego aktualizowania parametrów. W takich przypadkach tak jest jednakże konieczne wprowadzenie ważenia starych wejść i wyjść. Funkcja strat (2.16) umieszcza równą wagę na wszystkie dane. Pomiar zebrany dawno temu jest tak ważny jak ostatni pomiar. Nowszy pomiar może dawać większą wagę przez zamianę funkcji strat (2.16) do:

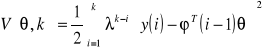
(2.18)

gdzie 0≤λ≤1 jest współczynnikiem zapominania. Typowa jego wartość wynosi 0,98. Dopóki wagi mają rozkład wykładniczy algorytm otrzymany jest nazywany rekursywną metodą najmniejszych kwadratów z wykładniczym zapominaniem. Formuły aktualizujące są tylko odrobinę zmodyfikowane:

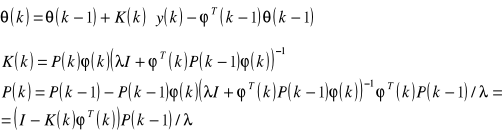
(2.19)

Algorytm RLS z punktu widzenia wykonawczego wygląda następująco:

1. Wybór wartości początkowych P(k),
   ,
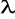
   ( macierz kowariancji, wektor przybliżonych parametrów oraz współczynnik zapominania)

2. Odczytanie nowych wartości y(k) i u(k) (sygnał wyjściowy obiektu oraz sygnał sterujący)

3. Wyliczenie z góry resztkowego błędu identyfikacji
   

4. Wyliczenie K(k) jak w wyrażeniu (3.23)

5. Obliczenie nowych parametrów estymacji
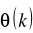
   3.23.

6. Obliczenie nowego współczynnika zapominania
   

jeżeli
<
_min wtedy
=
_min

jeżeli
>1 wtedy
=1

Dodatkowo parametr S₀ musi być z góry znany, jest on powiązany z kwadratem błędu identyfikacji.

7. Aktualizacja macierzy kowariancji 3.23

Jeżeli

8. Wykonania k=k+1 i powrót do kroku nr 2

Wartości
oraz początkowy współczynnik zapominania zależą od systemu oraz projektowanej szybkości konwergencji i stabilności. Wartość współczynnika zapominania przyrównujemy do jedności, macierz kowariancji maleje monotonicznie, pozwalając identyfikatorowi wzmocnienia wynosić zero. Ponadto, jeżeli punkt operacyjny jest naprawiony, czynnik
może być zero, i wtedy
, gdzie dla
<1 uczyni P(k) szybko wzrastającą, czyniąc identyfikator bardzo czułym na jakąkolwiek zamianę. To są powody, uzasadniający pojawienie się współczynnika zapominania w algorytmie identyfikacji. Jeżeli macierz kowariancji przekracza określoną wartość, współczynnik zapominania jest naprawiany
=1.

Poniżej przedstawiono kilka wyjaśnień rekursywnej metody najmniejszych kwadratów na podstawie [11]:

• Wektor
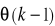
  i macierz P(k-1) obrazują wyniki estymacji przeprowadzonej od chwili (k-1), niezależnie od tego, jak duże jest k oraz ile danych pomiarowych już przetworzono.

• Nowa estymacja wektora
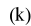
  jest otrzymana przez sumowanie iloczynu wektora korekcyjnego i skalara starej oceny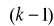
  .

• W przypadku e(k)=0 i dokładnej predykcji dla kroku (k-1) jest
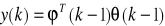
  i wtedy
  .

• Współrzędne wektora wagi k(k) są wagami, które określają wpływ błędu predykcji jednego kroku
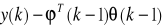
  na poszczególne składowe nowej oceny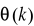
  .

• Zmniejszanie się wagi przywiązywanej do pomiarów odległych w czasie ma charakter wykładniczy.

• Zbieżność P(k) do macierzy zerowej sprawia, że dla λ=1 ocena
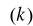
  nie nadąża za zmianami parametrów regulatora docelowego, które nastąpiły po rekurencji.

• Dla λ<1 nie istnieje granica dla P(k) przy k rosnącym w sposób nieograniczony; każda nowa macierz
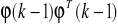
  , nawet przy bardzo dużych k, powoduje zmianę P(k).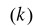
  nie będzie zbieżne, lecz będzie się cały czas zmieniać pod wpływem zakłócenia e(k). Z powyższego wynika możliwość nadążania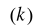
  za wolnymi zmianami prawdziwego wektora parametrów
  .

• Rekurencję rozpoczyna się przyjmując za wartości początkowe
  , P(0) = a I, a>>0.

Poniżej została opisana - również wykorzystywana w trakcie symulacji - metoda RLS z faktoryzacją UDU (RLS with UDU factorization):

Opiera się ona na zwykłej metodzie RLS 2.19. Rozwiązuje problem równania
które zazwyczaj w wyniku działania algorytmu RLS daje wyniki znacznie odbiegające od rzeczywistości (ujemna macierz P). P musi być określona dodatnio. Do tego służy algorytm UDU.

Określamy P jako

gdzie D jest macierzą diagonalną,

U - trójkątna (górna) macierz dla której elementy diagonalne wynoszą 1.

Niżej zdefiniowano macierze U(k-1), D(k-1) jako
i wprowadzono je do wzoru na P(k) 2.19:

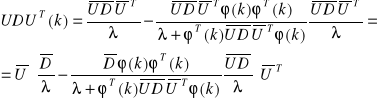
(2.20)

dla uproszczenia dokonano następujących podstawień:

na podstawie tego mamy:

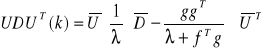
(2.21)

Wyrażenie między nawiasami sprowadzono do U_n,D_n,U^T_n i otrzymano:

(2.22)

Ostatnią z opisanych metod jest metodą EFRA (Exponencial Forgetting and Resetting Algorithm)

Metoda ta w teorii charakteryzuje się najszybszą zbieżnością. Wszystko jednak zależy od odpowiedniego doboru wartości początkowych. Jeżeli współczynnik zapominania obrany jest jako zbyt mały, wartości macierzy kowariancji P będą rosnąć w sposób niekontrolowany. Metoda EFRA jest skonstruowana w ten sposób, że utrzymuje wartości macierzy na bezpiecznym poziomie nie pozwalając algorytmowi „wybuchnąć”, a w konsekwencji utracić stabilność. Zabezpieczenie to włącza się, gdy jest to konieczne. Kiedy wystąpi problem z algorytmem, funkcja może sprawdzić wartość współczynników kowariancji i zakończyć aktualizację przed zakończeniem symulacji.

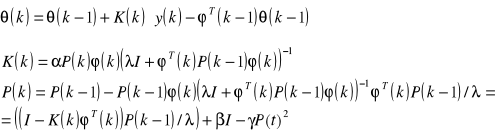
(2.23)

gdzie I - macierz identyfikacji,

,
- stałe.

Według tego algorytmu macierz kowariancji jest ograniczana jako:

gdzie
oraz
natomiast

Dla przykładu dla
= 0.5,
= 0.005 oraz
= 0.95,
=0.01 i
=10

2. Metody projektowe

Ostatnim krokiem w konstrukcji regulatora samonastrajającego jest procedura projektowa. Podstawowe regulatory samonastrajające są oparte na zasadzie równoważności. To implikuje wykorzystanie parametrów procesu z estymatora. Zasady „projektu” mogą jednakże być rozszerzone w kierunku niepewności obliczeń danych przez macierz P. Można to nazwać ostrożnym lub podwójnym kontrolerem.

Poniżej zostaną omówione dwie przykładowe zasady projektowe oparte na:

1. lokacji biegunowej (pole-placement) - PP;

2. minimalnej wariancji (minimum variance control) - MVC.

Na rysunku 2.3 przedstawiony jest regulator postaci:

(2.24)

Rys 2.3: Schemat blokowy regulatora z dwoma stopniami swobody.

Regulator składa się z części operacyjnej „rozkazu przesyłania”
oraz z ujemnego sprzężenia zwrotnego z częścią
. Z tego wynika, iż są dwa stopnie swobody.

1. Projekt lokacji biegunowej (lokowania biegunów PP)

Z równania (2.5) dla systemu pętli zamkniętej można uzyskać:

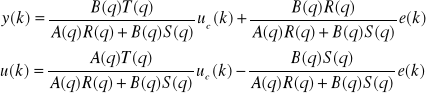
(2.25)

W poniższych rozważaniach elementy (q) zastąpiono * w celu lepszej czytelności i pokazano jak parametry w kontrolerze (2.24) mogą być wyznaczone metodą lokacji biegunowej dla zaprojektowania regulatora. Wielomian charakterystyczny pętli zamkniętej:

(2.26)

gdzie
jest dane jako parametr przez projektanta. Kluczową rzeczą jest teraz znalezienie wielomianów R^* i S^* które spełniają to równanie. Równanie (2.26) jest nazywane równaniem Diofantycznym z angielskiego „Diophantic”. Pożądany system pętli zamkniętej od sygnału odniesienia do wyjścia zdefiniowany w (2.5) określa, że muszą być spełnione następujące warunki:

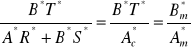
(2.27)

Ta procedura projektowa jest nazywana postępowym projektem modelu (model-following design), a także projektem biegunowym (pole-placement design) jeżeli tylko bieguny są określone. Model postępowy może być otrzymany zależnie od modelu, procesu oraz złożoności kontrolera.

Wielomian charakterystyczny (2.26) będzie w ogólności posiadać większy stopień jak model wielomianu
. To implikuje iż w (2.27) musi być biegun zerowy. Konsekwencje tego wyjaśniono poniżej. Wielomian B* procesu jest wstępnie sformułowany jako:

(2.28)

gdzie
odnosi się do procesu zer, które mogą być anulowane w projekcie. Te zera muszą być ulokowane wewnątrz koła. Zera odnoszące się do
, które nie mogą być anulowane muszą być czynnikiem
według formuły:

(2.29)

Dopóki zero
jest anulowane, musi być czynnikiem
. Wielomian charakterystyczny pętli zamkniętej ma zatem formę:

(2.30)

Wielomian
jest nazywany wielomianem obserwacji (observer polynomial) jest interpretowany jako dynamika stanu obserwacji. Wielomian obserwacji obrazuje, jak szybko system się odnowił po zakłóceniu.
jest określone przez projektanta i powinno być wielomianem stabilnym.

Dopóki
jest czynnikiem B* i
co wynika z (2.30) to jest także czynnikiem R*, co implikuje:

(2.31)

i równanie redukuje się do:

(2.32)

Ostatecznie wielomian T* jest dany jako:

(2.33)

Procedura projektowa może być sprowadzona do:

Dane: Podane wielomiany procesu: A*,
oraz wielomian obserwacji

Krok 1: Rozwiązanie równania diofantycznego (2.34) uwzględniając
i

Krok 2: Regulator jest dany jako (2.24) z
i

Równania Diofantyczne mogą być zawsze rozwiązane, jeżeli nie ma wspólnych współczynników pomiędzy wielomianami A* i B* i jeżeli sterownik (kontroler) wielomianowy posiada wystarczającą ilość parametrów.

2. Algorytm minimalnej wariancji (minimalnowariancyjny)

Większość metod projektowych może być interpretowanych jako lokacja biegunowa albo model predykcyjny. Kontroler minimalnej wariancji może być łatwo przedstawiony w takiej formie. Kontroler ten minimalizuje niezgodność na wyjściu procesu. W tym przypadku należy uwzględnić zakłócenie jako
(dodając z prawej strony (2.4)); gdzie C* jest stałym wielomianem i e(k) jest białym szumem. Kontroler minimalnej niezgodności otrzymujemy rozwiązując równanie diofantyczne:

(2.34)

używając prawa regulacji postaci:

(2.35)

Także algorytm LQG (Linear Quadratic Gaussian) może być interpretowany jako rozwiązanie specjalnej formy równania diofantycznego.

2. Projekt regulatorów samonastrajających STR

Projekt STR można sprowadzić do sekwencji następujących procedur:

WYMAGANIA: Określenie klasy kontrolera poprzez określenie wymagań systemu z pętlą zamkniętą

OSZACOWANIE: Oszacowanie parametrów procesu używając na przykład rekursywnego algorytmu najmniejszych kwadratów (2.21)

PROCEDURA PROJEKTU: Określenie parametrów kontrolera używając parametrów przybliżonego procesu jako prawidłowych. Projekt kontrolera jest zazwyczaj sprowadzony do równania diofantycznego,

STEROWANIE: Aktualizacja parametrów kontrolera na przykład w (2.24)

Oszacowanie, projekt i kroki regulacji są skończone w każdym interwale próbkowania. Zachowanie prostego, pośredniego algorytmu samonastrajającego opisano w przykładzie 2.1.

Przykład 2.1: Pośredni deterministyczny regulator samonastrajający

Przyjęto, że proces otwartej pętli jest opisany transmitancją ciągłą jako:

(2.36)

Nie ma zakłóceń wpływających na system i warunki są takie aby sterowany system mógł podążać za stałymi sygnałami odniesienia bez dużych uchybów. Próbkowanie systemu z przedziałem próbkowania h=0.5[s] daje opis próbkowanych danych w postaci:

(2.37)

W
proces jest „zerowy”. Zero jest w środku granicznej stabilności. Niech żądany system pracujący w pętli zamkniętej będzie określony jako: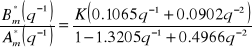
Prowadzi to do stałego w czasie systemu z częstotliwością naturalną
i tłumieniem
próbkowanego z okresem h=0.5. Wzmocnienie K jest wybrane tak, że stacjonarne wzmocnienie sygnału odniesienia do wyjścia jest równy 1,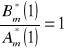
Regulator rozwiązujący projektowany problem będzie miał strukturę w postaci:

(2.38)

Rysunek 2.4 pokazuje wyjście i sygnał sterujący w procesie sterowanym przez kontroler samonastrajający. Sygnał odniesienia jest falą prostokątną. Jest widocznym, że wyjście zachowuje się dobrze już przy drugiej zmianie sygnału odniesienia. W czasie 100, warunki się zmieniają i tłumienie zmienia się z
na
. Pętla zamknięta odpowiada natychmiastową zmianą.

Rys 2.4. Proces wyjścia i wejścia, kiedy pośredni regulator samonastrajający jest używany do regulacji procesu. Sygnał odniesienia jest pokazany jako krzywa przerywana [1]

Model procesu posiada cztery nieznane parametry b₀, b₁, a₁ i a₂. Te parametry przybliżamy używając algorytmu RLS. Przybliżone parametry procesu są pokazane na rysunku 2.5. Przykład pokazuje, iż STR bardzo szybko znajduje dobre parametry kontroli i mogą być one zmieniane. Krótkotrwałość ustalania na początku zależy od wyboru wartości przedziału próbkowania w estymatorze.

Rys 2.5. Przybliżanie parametrów z rysunku 2.4 [1]

Pierwszy diagram:
- krzywa ciągła,
- krzywa przerywana

Drugi diagram:
- krzywa ciągła,
- krzywa przerywana

3. Bezpośrednie regulatory samonastrajające

Algorytm samonastrajający opisany poniżej polega na separacji pomiędzy estymacją a projektem. Krok projektu jest powtarzany dla każdego natychmiastowego próbkowania. W niektórych przypadkach może być wskazane unikanie wykonywania obliczeń w kroku projektu, na przykład z powodu obliczania ograniczeń czasowych. Aby to wykonać trzeba przekształcić pośredni regulator samonastrajający w bezpośredni STR. To powoduje, że parametry kontrolera są przybliżane w miejsce parametrów procesu. Jak dokonać tej reparametryzacji zostanie pokazane na regulatorze minimalnowariancyjnym.

Niech regulowany system będzie opisany jako:

(2.39)

Wymagania projektu są takie, aby minimalizować niezgodność sygnału wyjściowego d kroków w przód. Regulacja minimalnowariancyjna jest równoważna przewidywaniu wyjściowego sygnału i wybieraniu sygnału regulacji w taki sposób, że przewidziana wartość równa się zero albo innej żądanej wartości punktu.

Z [1] wiadomo, że wyjście może być zapisane jako:

(2.40)

gdzie F* i G* są uzyskane z równania diofantycznego (2.34) Przewidywanie d kroków wyjściowych naprzód jest dane jako drugie i trzecie wyrażenie po prawej stronie równania (2.41). Błąd przewidywania jest dany poprzez pierwszy wyraz po prawej stronie równania (2.41). Błąd przewidywania jest przemieszczeniem średniego stochastycznego procesu, który jest niezależny od przewidywanego wyjścia. Przewidziane wyjście wynosi zero jeżeli prawo kontroli jest wybrane zgodnie z (2.39). Używanie podstawowego prawa projektu było możliwe do zreparametryzowania modelu (2.40) w taki sposób, iż zreparametryzowany model wyraźnie zawiera parametry kontrolera. Parametry kontrolera mogą być więc przybliżone bezpośrednio. Używając regulatora minimalnowariancyjnego pętla zamknięta systemu staje się:

Ideą wychodzącą poza podstawowy bezpośredni regulator STR, jest przybliżanie parametrów w modelu predykcyjnym (z wyprzedzeniem czasowym)

(2.41)

i użycie kontrolera:

Więc parametry przybliżone są takie same jak parametry kontrolera i krok projektowy został wyeliminowany.

Przykład 2.2. Bezpośredni samonastrajający algorytm minimalnowariancjny

Założono proces bez pętli zwrotnej, opisany na próbkowanych danych modelu:

(2.42)

gdzie e(k) to biały szum o zakłóceniu 1.

Opóźnienie czasowe w systemie to d=1 Obliczyć należy parametry r₀ i s₀ w modelu

(2.43)

oraz użyć następującego regulatora:

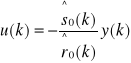
(2.44)

Optymalny regulator minimalnowariancyjny jest dany jako: u(k)=-0.2y(k) więc jest kontrolerem proporcjonalnym. Używając tego regulatora otrzymujemy wyjście y(k)=e(k), to znaczy wyjście powinno być białym szumem o zakłóceniu 1. Jedną drogą do porównania optymalnych i samonastrajających regulatorów jest porównanie skumulowanych funkcji strat.

(2.45)

Nachylenie (gradient) skumulowanej funkcji strat jest obliczeniem rozbieżności wyjścia. Rysunek 2.6 pokazuje funkcję strat kiedy algorytm samonastrajający oraz gdy optymalny regulator mminimalnowariancyjny są użyte.

Rys.2.6. Zakumulowana funkcja strat V(k) kiedy bezpośredni algorytm samonastrajający (linia ciągła) i optymalny regulator minimalnowawiancyjny (linia przerywana) są używane w procesie [1]

Po krótkim załączeniu chwilowe spadki funkcji strat są takie same, co wskazuje, że STR upodabnia się do optymalnego regulatora minimalnowariancyjnego. Można to również zobaczyć patrząc na wzmocnienie regulatora na rysunku 2.6.

Rys. 2.7. Wzmocnienie kontrolera
, kiedy jest używany algorytm samo-nastrajający (linia ciągła) Optymalne minimalne wzmocnienie kontrolera jest pokazane linią przerywaną [1]

1. Pozbywanie się zakłóceń

Zostanie pokazane jak może być zredukowany wpływ zakłóceń wprowadzając integratory oraz używając „metody śledzenia”.

Niech dany będzie proces:

(2.46.)

co jest drobnym przekształceniem równania (2.4). Sygnał
jest wejściowym zakłóceniem. Jeżeli na przykład jest to jednostkowy skok sygnału, wtedy w kontrolerze potrzebny jest integrator do eliminacji wpływu na to zakłócenie. W bezpośrednich regulatorach samonastrajających można poradzić sobie z tym na kilka sposobów. Jednym z nich jest obliczenie wielkości zakłócenia i kompensacja tego w kontrolerze. Ażeby to wykonać potrzebne jest aktywne nastrajanie cały czas, dopóki zakłócenie może się zmienić. Polecaną metodą [1] jest wprowadzenie integratora bezpośrednio do kontrolera. Może być to zrobione poprzez założenie, że wielomian R^* zawiera wyrażenie 1-q^-1. Można to wykonać w sposób bezpośredni tak dobrze, jak w algorytmach pośrednich.

W algorytmie pośrednim jest konieczna modyfikacja estymatora zanim zakłócenie zmieni relację pomiędzy wejściem a wyjściem. Zakłócenia wejściowe takie jak skok jednostkowy mają szczególnie zły wpływ na obliczany model z małą częstotliwością.

Zamodelujmy zakłócenie jako:

(2.47)

gdzie e(k) jest impulsem, spektrum impulsów lub białym szumem. Na przykład skok zakłócenia jest generowany przez:

(2.48)

Model (2.50) może być teraz opisany jako:

(2.49)

Wprowadzamy filtrowane sygnały y_f(k)=
y(k) i u_f(k)=
u(k) Otrzymujemy:

(2.50)

Nowy model ma błąd obliczeniowy e(k) zamiast
. Proces modelu może być teraz policzony z (2.51). Bazując na obliczeniach modelu, projekt regulatora jest wykonany przez rozwiązanie następującego równania diofantycznego:

(2.51)

i używając regulatora:

(2.52)

Regulator zawiera czynnik
, który będzie eliminował wpływ zakłócenia
.

W bezpośrednim algorytmie samonastrajającym minimalnowariancyjnym integrator może być wprowadzony przez zmianę modelu (2.46), a parametry regulatora obliczone z:

(2.53)

gdzie
=u(k)-u(k-1) i używając kontrolera

(2.54)

zawierającego integrator.

W wielu przypadkach jest możliwe zmierzenie zakłócenia wpływającego na system. Typowym przykładem jest kontrola temperatury wewnątrz pomieszczeń. Poprzez mierzenie także zewnętrznej temperatury, możliwe jest używać tego sygnału do kompensacji na zmiany zewnętrznej temperatury przed wpływem tego zakłócenia na system wewnętrzny. Jedną drogą do wprowadzenia postępowości w STR jest operowanie bezpośrednim algorytmem. Obliczany model jest zmieniany z (2.46) do:

(2.55)

gdzie
jest wymiernym zakłóceniem.

Kontroler jest reprezentowany jako:

(2.56)

Pierwsza część kontrolera jest pętlą zwrotną z mierzonego y(k), natomiast druga jest postępowa od mierzonego zakłócenia. Postępowość jest w ogólności bardzo przydatna w STR. Do zrobienia efektywnej postępowości jest konieczne posiadanie dobrego modelu procesu. Przez kombinację pomiaru zakłócenia i właściwości samonastrajających kontrolera jest możliwa eliminacja większości zakłóceń zanim osiągną wyjście procesu.

4. Uwagi

Opisano podstawowe idee regulatorów samonastrajających pokazując, że układy STR są właściwie nieliniowe. Nieliniowość tyczy się części estymującej i zmieniającej parametry w regulatorze. To powoduje, iż analiza układów STR jest bardzo skomplikowana. Regulatory samonastrajające posiadają dwie pętle i są konieczne badania stabilności oraz zbieżności właściwości systemu pętli zamkniętej. Jest to trudne zadanie ze względu na wzajemne oddziaływanie dwóch pętli kontroli. Aby ominąć ten problem należy rozdzielić czasowo obie pętle.

REGULATOR SAMONASTRAJAJĄCY STR 23

(2.17)

---