OBLICZENIA ZWARCIOWE W SIECIACH
Rodzaje zwarć
.
Przyczyny zwarć:
elektryczne
nieelektryczne
Skutki zwarć
cieplne i
dynamiczne.
Według statystyk częstość występowania różnych rodzajów zwarć przedstawia się następująco:
jednofazowe 65 %,
podwójne zwarcie doziemne około 20 % (dwa 1-fazowe),
dwufazowe około 10 %,
trójfazowe 5 %.
Elementy obwodów zwarciowych
Przy obliczaniu schematów zastępczych obwodów zwarciowych należy wziąć pod uwagę następujące elementy:
Sieć zasilająca
Transformator
Generator synchroniczny
Linie napowietrzne i kablowe
Dławik
Silniki indukcyjne - uwzględnia się jeśli suma prądów znamionowych silników jest większa od 1%
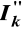
obliczonego bez udziału silnikówSymetryczny początkowy prąd zwarciowy
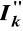
Prąd zwarciowy szczytowy ip
Symetryczny prąd zwarciowy wyłączeniowy Ib:
dla zwarć odległych Ib = Ik'',
dla zwarć w pobliżu generatora Ib = μIk'', gdzie μ należy określić z normy.
Zastępczy cieplny prąd zwarciowy Ith
Macierz admitancji gałęziowych [Yg] posiada tylko przekątną główną;
wektor prądów źródłowych gałęzi [Jg];
Macierz strukturalna układu -
Macierz (wektor) prądów gałęziowych:
macierz potencjałów węzłowych:
macierz admitancji węzłowych:
macierz prądów węzłowych:
Mamy 7 węzłów liniowo niezależnych,
Potencjały węzłów zasilających są znane, są sobie równe
Przy zwarciu 3-fazowym U4=0,
Należy obliczyć potencjały węzłów U1, U2, U3 i prądy płynące w obwodzie.
sieć |
cmax |
cmin |
230/400 V |
1,00 |
0,95 |
inne |
1,05 |
1,00 |
SN,WN,NN |
1,1 |
1,0 |
a) przyłączony bezpośrednio do sieci, bez transformatorów pośredniczących
b) generator synchroniczny w bloku energetycznym
Przebieg prądu zwarciowego
Rozpatrzymy obwód obciążony impedancją Zo, do którego doprowadzone jest napięcie sinusoidalne o wartości chwilowej wynoszącej ![]()
Rys.12.3. Przykładowy obwód zwarciowy
Dla celów doboru aparatury elektroenergetycznej do warunków zwarciowych należy wyznaczyć charakterystyczne parametry prądu zwarciowego. Na podstawie normy PN -IEC 60909-0: (2002)
Rys.12.4. Przebieg prądu zwarciowego przy zwarciu w pobliżu generatora: Ik”- prąd zwarciowy początkowy, ip - prąd udarowy, Ik - ustalony prąd zwarciowy, iDC - składowa nieokresowa prądu zwarciowego, A - wartość początkowa składowej
Parametry prądów zwarciowych
Zgodnie z normą rozróżniamy dwa rodzaje zwarć:
Zwarcia odległe od generatorów
Zwarcie w pobliżu generatora
Parametry zwarciowe przy zwarciu trójfazowym:
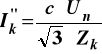
(12.1
![]()
Współczynnik udaru χ odczytuje się z wykresu w zależności od Xk/Rk lub Rk/Xk.
![]()
gdzie: m - uwzględnia wpływ cieplny składowej nieokresowej prądu zwarcia,
n - uwzględnia wpływ cieplny składowej okresowej prądu zwarcia.
Urządzenie elektryczne ma dostateczną wytrzymałość cieplną zwarciową gdy znamionowy prąd zwarciowy Ithn jest większy od zastępczego cieplnego prądu zwarciowego Ith:
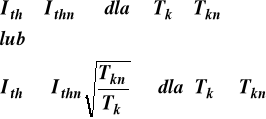
(12.1
gdzie: Tkn [s] - znamionowy czas trwania zwarcia
Wytrzymałość cieplna przewodów podczas zwarcia jest dostateczna gdy:

(12.1
gdzie: jth - gęstość zastępcza cieplna,
jthn - gęstość zastępcza prądu zwarciowego 1-sekundowego.
Obliczanie prądów zwarciowych
Jeżeli zwarcie zasilane jest z jednego źródła to do obliczeń prądu zwarciowego wystarcza znajomość zastępczej impedancji zwarciowej i obliczenia są stosunkowo proste. W przypadku zasilania zwarcia z wielu źródeł konieczna jest znajomość rozpływu prądów w obwodzie zwarciowym.
Obliczanie zwarć zasilanych z jednego źródła
Przykład 12.1:
Obliczyć charakterystyczne wartości prądu zwarciowego przy zwarciu w pkt. 3 (w-otwarty), układ jest przedstawiony na rysunku 12.6.
Dane: transformator o mocy St = 31,5 MVA, przekładni ϑ = 110/6,3 kV, Δuz%= 10,5 %, linia napowietrzna AFL 3x240, o długości 4 km i reaktancji jednostkowej X'L=0,1 Ω/km. Moc zwarciowa na szynach 110 kV wynosi Sz = 1500 MVA.
Zgodnie z rys.12.6b obliczamy parametry schematu zastępczego:
Wyznaczanie rozpływu prądów zwarciowych metodą potencjałów węzłowych
W przypadku układów zasilanych z wielu źródeł do rozpływu prądów zwarciowych stosujemy metodę potencjałów węzłowych przy której przyjmujemy pewne uproszczenia
Przykładowy układ elektroenergetyczny:
Rys.12. 7. Układ do wyznaczania prądu zwarciowego: a) układ zasilania, b) schemat zastępczy
Wprowadzamy pojęcia:
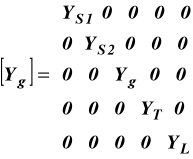
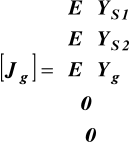
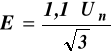
(12.1

(12.1
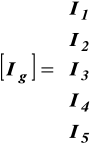
(12.1
Obliczenia: Ponieważ pomijamy obciążenia więc suma prądów w węzłach Ik = O, stąd:
[Ig ] =[Jg] - [Yg][Ug]
Rys.12.8. Prądy źródłowe i gałęziowe
[Ug] = [B]T[Uw] → [B][Yg][B]T[Uw] = [B][Jg] (12.1
[Yw] = [B][Yg][B]T [Yw][Uw] = [B][Jg] (12.1
[Iw] = [B][Ig] (12.1
Stąd równanie metody potencjałów węzłowych:
[Yw][Uw] = [Iw] (12.1
Jego rozwiązanie
[Uw] = [Yw]-1[Iw] (12.1
Jeśli obliczymy potencjały w węzłach, obliczymy napięcie gałęziowe [Ug] i prądy w interesujących nas gałęziach [Ig].
Przykład 12.2:
Dany jest układ przedstawiony na rys.12.9. Znając impedancje zastępcze poszczególnych gałęzi obliczyć prąd przy zwarciu 3-fazowym na szynach 4.
Rozwiązanie:
i wynoszą ![]()
Jeśli znamy potencjały we wszystkich węzłach to zgodnie z metodą
potencjałów węzłowych prąd w k-tym węźle można obliczyć z zależności:
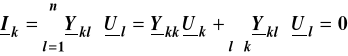
(12.1
21
Rys.12.5.Współczynnik χ
Wyszukiwarka
Podobne podstrony:
9wardahalla-elen-tekst, Przwatne, Studia, Semestr 4, Elektroenergetyka, Wykłady
badanie rezystancji izolacji stanowiska - protokol, Przwatne, Studia, Semestr 4, Elektroenergetyka
3-L88, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
3-L44, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
3-L33, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
3-L22, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
3-L11, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
3poleteoria, Przwatne, Studia, Semestr 4, Elektroenergetyka, materiały
sprawko 2 elektrotechnika, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab
sprawko3, Przwatne, Studia, Semestr 4, Elektronika, Sprawka z elektroniki, Sprawka z elektroniki, sp
c1 teoria, Przwatne, Studia, Semestr 4, Elektroenergetyka, materiały
c2 teoria, Przwatne, Studia, Semestr 4, Elektroenergetyka, materiały
tranzystor bipolarny, Przwatne, Studia, Semestr 4, Elektronika, Sprawka z elektroniki, Sprawka z ele
3-L55, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
badanie rezystancji izolacji stanowiska - protokol, Przwatne, Studia, Semestr 4, Elektroenergetyka
3-L88, Przwatne, Studia, Semestr 4, Elektroenergetyka, Lab, wachta, 3 4, lab3
więcej podobnych podstron