1 def wielk podst.

Naprężeniem p w danym punkcie B przekroju danego ciała stałego nazywamy granicę, do której dąży iloraz siły wewnętrznej ΔPw przez wyodrębnione pole ΔA tego przekroju, gdy pole to dąży do zera.

,

Wektor naprężenia można rozłożyć na dwie składowe:

Wyznaczenie rozkładu sił wewnętrznych na powierzchni przekroju określonych wymienionymi naprężeniami jest zadaniem statycznie niewyznaczalnym, a jego rozwiązanie wymaga uwzględnienia odkształceń danego ciała. Wartość naprężenia w danym punkcie ciała zależy nie tylko od obciążenia, ale również od orientacji rozpatrywanego przekroju. Przez każdy punkt można poprowadzić dowolną liczbę przekrojów. Konieczne jest zatem wprowadzenie pojęcia odnoszącego się do ogółu naprężeń

Stanem naprężenia nazywamy ogół naprężeń występujących w różnych punktach i przekrojach rozpatrywanego ciała.

Pod wpływem obciążeń ciało stałe odkształca się, a poszczególne jego punkty przemieszczają się względem określonego układu odniesienia.

Przemieszczeniem
punktu M ciała nazywamy wektor, którego początkiem jest ten punkt przed odkształceniem ciała, a końcem punkt M' znajdujący się w nowym położeniu po odkształceniu.

u,v,w - wartości algebraiczne składowych przemieszczenia

- wersowy osi układu

,

- średnie odkształcenie względne na kierunku wyznaczonym przez odcinek AB

- liniowe odkształcenie względne w punkcie A

Odkształcenie
uważamy za dodatnie, gry
, tzn. odległość pomiędzy punktami wzrasta.

- kąt odkształcenia postaciowego (wg rysunku) - kąt o jaki zmienia się wzajemne położenie początkowo wzajemnie prostopadłych osi.

Kąt
uważa się za dodatni, gdy kąt pomiędzy osiami maleje po odkształceniu

2. ROZCIĄGANIE I ŚCISKANIE PRĘTÓW PROSTYCH

Przekroje płaskie i prostop do osie pręta przed deformacją pozostają plaskie i prostop. do osi pręta po deformacji - hip. plaskich przekrojow.

1. warunki równowagi - na nieważki pręt prosty o stałym przekroju A działa jedna siła P, która powoduje powstawanie w przekrojach poprzecznych wyłącznie naprężeń normalnych σ.

, jeśli σ = const

2. warunki geometryczne - pod wpływem siły pręt odkształca się. Zgodnie z przyjętymi założeniami, mechanizm odksztalcenia można opisać jako przemieszczenia przekrojów poprzecznych wzdłuż osi pręta przy zachowaniu ich płaskości i prostopadłości do osi.

Wydłużenie względne ε zwane również wydłużeniem jednostkowym lub odkształceniem wzdłużnym określone jest wzorem:
. Jak wynika z definicji, jest to wielkość niemianowana. W przypadku ściskania, analogiczną wartość nazywamy skróceniem względnym

Z założenia o płaskości przekroju wynika, że dla danego przekroju poprzecznego ε = const.

Całkowite wydłużenie pręta oblicza się ze wzoru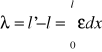
. Przy założeniu, że ε = const(x) otrzymujemy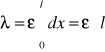
,

Podczas odkształcenia zmieniają się nie tylko wymiary podłużne pręta, ale również jego średnica. Zakładając, że zmiany wymiarów poprzecznych są równomierne, można określić następującą wielkość, zwaną wydłużeniem poprzecznym pręta:
.

W przypadku rozciągania d jest większe od d', czyli ε'<0.

3. związki fizyczne - (zalezn miedzy naprez i odksztalc.)w celu wyznaczenia wydłużeń, w zależności od wartości obciążenia konieczne jest ustalenie prawa fizycznego dotyczącego związku pomiędzy naprężeniami i odkształceniami.

3.Prawo Hookea dla preta rozc

wydłużenie jest wprost proporcjonalne do naprężenia, które je spowodowało.

E - moduł sprężystości podłużnej (moduł Younga), E=[
]=[Pa]

Wielkość ta jest cechą danego materiału i charakteryzuje jego odkształcalność. Wydłużenie poprzeczne jest również proporcjonalne do naprężenia, a stosunek
jest liczbą stałą, zależną od właściwości materiału.

,
[ni] - współczynnik Poissona,

Przy obowiązującym założeniu o płaskości przekrojów, ze związku
wynika, że naprężenie σ musi mieć wartość stałą w danym przekroju, a zatem z równania
wynika związek
.

Wydłużenie całkowite wyznaczone ze wzoru
, po uwzględnieniu powyższych związków wynosi
,EA - sztywność pręta na rozciąganie

4.Wykres rozc opis def poszcz napr odksz wyznaczyc i zdef granice

Statyczna proba rozc uważana jest za podst doświadcz w W M, mające doprowadzić do określenia właściwości mech materiału. Próba realizowana jest przy użyciu maszyny wytrzym, zwanej zrywarką. Specjalna próbka poddawana jest rozciąganiu siłą, której wartość wzrasta powoli z prędkością określoną odpowiednią normą. Zakłada się, że odpowiadające określonym naprężeniom odkształcenia pojawiają się natychmiast po zadziałaniu obciążenia, czyli w każdym momencie istnieje równowaga w stanie naprężenia i odkształcenia. Próbę poprzedza dokładny pomiar charakterystycznych wymiarów próbki.

S₀, S_u - wielkości przekroju poprzecznego przed i po odkształceniu

W wyniku próby otrzymujemy wykres zależności P-Δl, P - siła rozciągająca ;

W celu umożliwienia porównania otrzymanych wyników, dla różnych materiałów i różnych rozmiarów próbek, przedstawia się otrzymaną zależność w układzie σ-ε.

.

w początkowym stadium próby aż do przekroczenia przez siłę rozciągającą pewnej granicznej wartości, zależność jest liniowa (odcinek 0A). Obowiązuje tu prawo Hooke'a.

- granica proporcjonalności: największa wartość naprężenia, przy której zachodzi jeszcze wprost proporcjonalna zależność pomiędzy napr i odksztalceniem - granica stosowalności prawa Hooke'a.

Dalszemu wzrostowi obciążenia towarzyszy coraz szybszy przyrost odkształcenia, a wykres przybiera postać łuku. Po przekroczeniu wartości siły odpowiadającej punktowi B, próbka doznaje odkształceń trwałych.

- granica sprężystości: największa wartość naprężenia, przy której nie zachodzą jeszcze odkształc trwałe.

Ze względu na trudności w oddzielnym pomiarze powyższych wielkości przyjmuje się tzw. umowną granicę sprężystości.

- wartość siły odpowiadająca odkształceniu trwałemu o 0,05%

W przypadku stosowania umownej granicy sprężystości, jest ona kresem stosowalności prawa Hooke'a.

=

Po przekroczeniu wartości siły odpowiadającej punktowi C wykresu, materiał osiąga stan płynięcia, doznając przyrostów wydłużenia przy braku przyrostów siły.

- granica plastyczności - wartość naprężenia, przy której próbka zaczyna doznawać przyrostu odkształcenia przy braku przyrostu obciążenia.

Charakterystyka σ-ε na odcinku CD jest pofalowana wskutek pojawiających się poślizgów pomiędzy cząstkami materiału. W związku z tym Polska Norma określa pojęcie górnej i dolnej granicy plastyczności.

Dla celów praktycznych definiuje się wielkość nazywaną umowną granicą plastyczności

-wart siły odpowiadająca odkształceniu trwałemu o 0,2%

Do dalszej deformacji próbki konieczny jest przyrost obciążenia.

Pm-najw wart sily obciazajacej probke

- wytrzymałość na rozciąganie: wartość naprężenia odpowiadająca maksymalnej wartości siły rozciągającej próbkę.

W ostatniej fazie eksperymentu na próbce pojawia się przewężenie. Jej rzeczywisty minimalny przekrój poprzeczny jest zatem znacznie mniejszy niż wartość S₀. Linia DE' wykresu odpowiada naprężeniu rzeczywistemu, tj. odniesionemu do rzeczywistego, aktualnego pola powierzchni przekroju poprzecznego.

Naprężenia dopuszczalne - współczynnik bezpieczeństwa

Wzrost naprężeń i odkształceń powoduje zmiany w stanie fizycznym ciała, które prowadzą do odkształceń trwałych lub zniszczenia spójności materiału. Zmiany te określa się jako wytężenie materiału.. W przypadku rozciągania lub ściskania prętów prostych miarą wytężenia jest naprężenie normalne σ w przekr poprzecz pręta.

W poprawnie zaprojektowanej konstrukcji wytężenia nie może osiągnąć stanu niebezpiecznego, a zatem w przypadku pręta rozciąganego naprężenie σ nie może osiągnąć wyznaczonej eksperymentalnie wartości niebezpiecznej, za którą w zależności od warunków można uznać granicę plastyczności R_e, wytrzymałość na rozciąganie R_M

Maksymalną wartość, jaką może osiągnąć naprężenie σ nazywamy naprężeniem dopuszczalnym.

(kc) n - współcz bezpieczeństwa; n > 1

kr - wytrz dopusz na rozc

kc - wytrz dop na ścisk

Właściwy dobór współczynnika bezpieczeństwa jest jednym z podst zagadnień w procesach projektowania elementów konstrukcji. Jego wartość musi być na tyle duża, by uwzględnić prawdopodobieństwo zupełnie przypadkowych odstępstw od warunków przyjętych za podstawę obliczeń. Przyjęcie zbyt dużej jego wartości prowadzi z kolei do przewymiarowania konstrukcji i związanego z tym zbędnego przyrostu jej masy oraz nadmiernej materiałochłonności.

Podstawą obliczeń prętów poddanych działaniu siły osiowej jest równanie

Warunek wytrzymałościowy
Warunek sztywnościowy:

Całkowite wydłużenie (skrócenie) pręta nie może przekroczyć wart dop, umożliwiającej poprawną pracę elem konstr:

5 Ozn skladowych 3 kierunk stanu napr,tensor napr

1. Oznaczenia składowych naprężeń. Tensor naprężeń.

W celu określenia stanu naprężenia w ciele konieczna jest znajomość naprężenia w dowolnym przekroju ciała w dowolnym jego punkcie. W celu oznaczenia składowych stanu naprężenia w punkcie wyodrębnia się wokół niego nieskończenie mały prostopadłościan, nazywany prostopadłościanem elementarnym.

Jeżeli wymiary badanego prostopadłościanu są nieskończenie małe, to jednoimienne i równoległe naprężenia dla każdej pary ścian równoległych różnią się o nieskończenie małą wartość, a zatem można przyjąć, że są jednakowe.

- naprężenia styczne

W prostopadłościanie elementarnym występuje 9 składowych naprężeń: 3 normalne i 6 stycznych.

Składowe naprężeń stycznych prostopadłe do krawędzi przecięcia się dwóch przekrojów elementarnych, wzajemnie prostopadłych są zawsze równe. Oznacza to, że:

Składowe naprężenia określające stan naprężenia w rozpatrywanym punkcie można przedstawić w postaci macierzy, zwanej tensorem naprężeń:

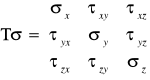
Można zatem stwierdzić, że stan naprężenia w punkcie jest w pełni określony, jeżeli znany jest tensor naprężeń dla tego punktu.

Dla każdego określonego stanu naprężenia można wyznaczyć trzy wzajemnie prostopadłe osie określające trzy kierunki główne. W odpowiadających im przekrojach występują wyłącznie naprężenia normalne zwane głównymi. Orientacja kierunków głównych oraz wartości naprężeń głównych nie są zależne od przyjętego, wyjściowego układu współrzędnych i są niezmiennikami stanu naprężenia.

Znajomość kierunków naprężeń głównych umożliwia określenie stanu naprężenia tylko 3 składowymi. Wartości naprężeń głównych spełniają nierówności:

- naprężenie max

- naprężenie min

5.Koło mohra dla plaskiego stanu napr rys wzory trans

Z liniowych na glowne

a) D:
Sz:

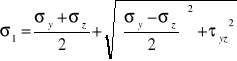
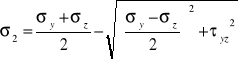
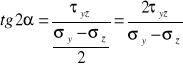
z gl na liniowe

b) D:
Sz:

7 Uogolnione prawo Hookea dla plask st napr wypr wzory

Rozpatrujemy kostkę sześcienną o wymiarach jednostkowych, poddaną działaniu płaskiego stanu naprężenia. Stosując zasadę superpozycji, powyższy stan naprężenia można wyrazić jako dwa stany składowe:

Odkształcenia kostki poddanej jednorodnemu działaniu naprężeń σ₁, σ₂ są superpozycją odkształceń w obu powyższych stanach.

- uogólnione prawo Hooke'a dla płaskiego stanu naprężeń

8 Uproszczona analiza kier st napr hip.wytrzym.

Rozpatrujemy kostkę sześcienną poddaną działaniu naprężeń głównych
, przy czym zachodzą nierówności:
.

Trójwymiarowy stan naprężenia można potraktować jako superpozycję trzech stanów płaskich dla trzech wzajemnie prostopadłych płaszczyzn. W każdym z tych przypadków stan naprężenia możemy zilustrować za pomocą koła Mohra.

Można udowodnic, że przy równoczesnym działaniu wszystkich trzech naprężeń głównych, naprężenia w dowolnym przekroju określone będą odpowiednim punktem N, znajdującym się w obszarze zakreskowanym, ograniczonym trzema kołami Mohra, zbudowanymi dla naprężeń głównych.

Wartości naprężeń w przekroju N określone są przez punkt N na rysunku. Największe naprężenie styczne
wystepuje w przekroju prostopadłym do płaszczyzny wyznaczonej przez kierunki naprężeń głównych
i
, a normalna tego przekroju tworzy kąt 45° z kierunkami naprężeń
i
.

Hip wytrz.

- naprężenie zredukowane

Hipotezy wytrzymałościowe są formułami określającymi kryteria oceny stanu wytężenia materiału w złożonym (trójwymiarowym) stanie naprężenia w celu ilościowego porównania takiego stanu przypadkiem prostym, jakim jest rozciąganie.

Naprężeniem zredukowanym
(
) nazywamy naprężenie otrzymane po zastosowaniu przyjętej hipotezy wytrzymałościowej dla trójkierunkowego stanu naprężenia, które jest równoważne z naprężeniem rozciągającym w jednowymiarowym stanie naprężenia.

1) hipoteza
(Rauchine'a)-hip najwiekszych napr normalnych

W myśl tej hipotezy naprężenia
i
nie mają żadnego wpływu na wytężenie materiału,jeżeli sa tylko mniejsze od
. Hipoteza ta ma znaczenie historyczne, bywa czasem stosowana dla mater kruchych np. kamien

2) hipoteza największego wydłużenia względnego
(de Saint Vernanta)

Hipoteza ta daje lepszą zgodność z wynikami doświadczeń od hipotezy
. Była powszechnie stosowana w początkach XX w., obecnie stosowana dla niektórych materiałów kruchych.

3) hipoteza największych naprężeń stycznych
(Coulomba)

Hipoteza wykazuje dużą zgodność z doświadczeniem (szczególnie dla materiałów plastycznych) i bywa obecnie szeroko stosowana.

4) hipoteza Huber-Mises-Henckig (H-M-H)

W myśl tej hipotezy o wytężeniu materiału decyduje największa energia odkształcenia postaciowego.

Wartość wynikająca z hipotezy Hubera wykazuje największą zgodność z wynikami doświadczeń dotyczących materiałów plastycznych wykazujących jednakowe własności na rozciąganie i ściskanie (stale, aluminium,)

Hipoteza
bywa stosowana na równi z hipotezą Hubera, ponieważ w większości przypadków obie hipotezy dają zbliżone wyniki.

9 Czyste zgin analiza napr i odksz wypr wzor na rozklad mom norm -war wytrz

Jeżeli siły wewnętrzne redukują się do wektora momentu gnącego Mg, to mówimy że w przekroju tym występuje czyste zginanie.

Jeżeli oprócz momentu gnącego w przekroju występuje również siła tnąca T, to mamy do czynienia z przypadkiem zginania z udziałem sił poprzecznych

Rozpatrujemy pręt o prostokątnym przekroju poprzecznym, poddany czystemu zginaniu:

W odkształconym pręcie przekroje poprzeczne płaskie i prostop do osi preta przed odkształceniem pozostają płaskie po odkształceniu. Włókna D, D₁ ulegają wydłużeniu, a włókna B, B₁ - skróceniu. Długości włókien C, C₁ położonych w połowie przekroju nie ulegają zmianie. W strefie włókien B, B₁ pręt ulegnie rozszerzeniu, a w strefie włókien D, D₁ - zwężeniu. Pierwotnie prostokątny przekrj poprzecz przybierze kształt zbliżony do trapezowego.

Oprócz hipotezy płaskich przekrojów, w mocy pozostaje druga hipoteza stwierdzająca, że względne odkształcenia poprzeczne pręta są w każdym punkcie(ni)
-razy mniejsze od odkształceń podłużnych, zatem związek pomiędzy odkształceniami jest identyczny, jak w przypadku zwykłego rozciągania lub ściskania. Zakłada się, że włókna równoległe do osi pręta poddawane są jednokierunkowemu stanowi naprężenia i nie wykazują żadnych wzajemnych oddziaływań poprzecznych. Włókna położone w poziomej płaszczyźnie symetrii nie ulegają ani skróceniu, ani wydłużeniu, a zatem naprężenia w tych włóknach są równe zero. Powierzchnię utworzoną z tych włókien nazywamy warstwą obojętną. Krawędź przecięcia się warstwy obojętnej z płaszczyzną przekroju poprzecznego pręta zginanego nazywamy osią obojętną tego przekroju.

Długość odcinka
po deformacji nie uległa zmianie i wynosi
. Włókno
przed odkształceniem miało długość równą
, natomiast po odkształceniu:
.

Wydłużenie względne włókna wynosi:

Zgodnie z prawem Hooke'a, włókno to rozciągane jest naprężeniem
, więc

Promień krzywizny ρ jest stały, a zatem naprężenia w poszczególnych punktach przekroju belki zginanej zmieniają się proporcjonalnie do odległości tych punktów od warstwy obojętnej.

Naprężenia te muszą zapewniać równowagę statyczną rozpatrywanej części pręta.

Elementarna siła wynosi

Po podstawieniu zależności
, otrzymujemy:

Z warunku równowagi statycznej wynika, że suma sił elementarnych w całym przekroju pręta równa się 0.

Ponieważ
, zatem równanie jest spełnione gdy
, a zatem gdy moment statyczny

pola przekroju względem osi obojętnej jest równy 0.

Oznacza to, że oś obojętna przekroju musi pokrywać się z jego osią centralną, a zatem warstwa obojętna przechodzi przez środki ciężkości przekrojów poprzecznych. Ze względu na małe odkształcenia, przyjmuje się że oś obojętna jest prostą, a warstwa obojętna - powierzchnią walcową.

Moment elementarnej siły dP względem osi obojętnej wynosi
.

Z warunku równowagi momentów dla rozpatrywanej części otrzymujemy:
=
dA

Z zależności
oraz powyższej otrzymujemy:

otrzymujemy:

Z równania
otrzymujemy

Porównując stronami powyższe równania: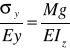
, ostatecznie:

- naprężenie normalne w dowolnym punkcie przekroju

Z powyższego wyrażenia wynika, że największe wartości przyjmują naprężenia w włóknach najbardziej oddalonych od osi obojętnej. Jeżeli odległości skrajnych włókien ściskanych i rozciąganych od osi obojętnej są równe, to wartości największych naprężeń rozciągających i ściskających są równe. Dla uproszczenia nazywamy je naprężeniami gnącymi.

rys

- naprężenie gnące

(wskaźnik wytrzymałości przekroju na zginanie)

k_g - wytrzymałość dopuszczalna na zginanie

- jeżeli
, to

- jeżeli
, to:

,

,

10 Rown rozn linii ugiecia (skad się biora jak się calk)

Analizujac odksztalcenia belki poddanej czystemu zginaniu można stwierdzic ze wskutek dzialania momentu tnacego zachodzi wzajemny obrot względem osi obojetnych uprzednio rownoleglych przekrojow.Odksztalcenia te powoduja zakrzywienie czyli ugiecie prostej osi preta

Rys

W ukladzie plaskim w którym os x pokrywa się z nieodksztalcona osia preta linie ugiecia opisuje rownanie y=f(x)

Krzywizna belki

Wzor na krzywizne linii plaskiej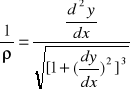

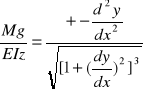
W praktyce stosuje się pewne uproszczenia. Jeżeli naprezenia w zadnym przekroju belki zginanej nie przekraczaja granicy proporcjonalnosci to kat nachylenia do stycznej jest maly a zatem wielkosc (dy/dx)^2 jest znacznie mniejsza od jednosci. Przyjmujemy:

Znak +- zalezy od sposobu ustalenia znaku momentu gnacego i po orientacji osi znaku odniesienia

EIz

Rownanie to przyjmuje się za punkt wyjscia do wyznaczania przemieszczen:

EIz
dx + C

EIzy=-

Rozniczkowe rownanie linii ugiecia mozna sformulowac dla kazdego przedzialu belki dla ktorego okreslona jest funkcja Mg. Liczba rownan odpowiada liczbie przedzialow zmiennosci.Stale C i D wyznacza się z okreslonych warunkow których musza odpowiadac przemieszczenia na brzegach przedzialu(war brzegowe). Sa one zalezne od rodzaju podpor i ogolnego warunku ciaglosci linii ugiecia. Warunek ten dla punktow stanowiacych granice przedzialu ciaglosci wyraza się jako warunek nie rozdzielnosci przemieszczen katowych oraz przemieszczen liniowych.

Calkowanie linii ugiecia met analit

Wyzn max ugiecie belki pokazanej na rys

0<x<

Mgx= (
War brzegowe:

EIz
-(

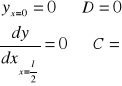
f=

EIz
(
+C

Eizy=-(
+Cx+D

11 M Clebscha opis zaloz na przykladzie wykazac rownosc stalych calkowania

Mgx5=

EIz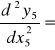
-

EIz
-
+C5

EIz
-

EIz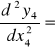
-

EIz
-
+

EIz
=-
+

EIz
=
EIz
=
EIz
=

Z warunku ciaglosci odksztalcen wynika:

=

Dokonujac analogicznych porownan dla pozostalych granic ptrzymujemy

C1=C2=C3=C4=C5=C

D1=D2=D3=D4=D5=D

Z powyzszych rozwazan wynika ze poszukujemy tylko 2 stalych calkowania należy wiec skorzystac z 2 warunkow brzegowych w celuich wyznaczenia

---