6. Funkcje kwadratowe

Funkcją kwadratową lub trójmianem kwadratowym nazywamy funkcję określoną wzorem

gdzie a, b, c są współczynnikami rzeczywistymi, przy czym
Powyższy wzór definiujący f nazywa się postacią ogólną funkcji kwadratowej.

Wykonajmy następujące przekształcenie:

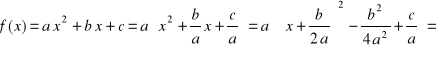
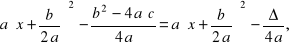
gdzie
Liczba
nazywa się wyróżnikiem trójmianu kwadratowego, a wzór

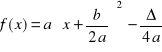
postacią kanoniczną tego trójmianu.

Powyższa postać kanoniczna funkcji kwadratowej pozwala na otrzymanie w prosty sposób wykresu tej funkcji poprzez przesunięcie równoległe o wektor
wykresu jednomianu kwadratowego postaci
Ponieważ wykresem jednomianu kwadratowego jest krzywa zwaną parabolą o wierzchołku w początku układu współrzędnych, to wykresem funkcji kwadratowej
jest parabola o wierzchołku w punkcie
Ramiona tej paraboli są skierowane do góry, jeśli
, i skierowane ku dołowi, gdy
Rozchylenie gałęzi paraboli zależy od wartości
. Im wartość bezwzględna a jest mniejsza, tym bardziej gałęzie paraboli są odchylone od osi OY.

Z powyższych faktów wynika, że:

Jeżeli
, to funkcja kwadratowa
przyjmuje dowolnie duże wartości, a w punkcie
osiąga wartość najmniejszą (minimum) równą

Jeżeli
, to funkcja kwadratowa
przyjmuje dowolnie małe wartości, a w punkcie
osiąga wartość największą (maksimum) równą

Przykład. Rozwiążemy równanie

.

Rozwiązanie. Aby skorzystać z posiadanych wiadomości o funkcji kwadratowej, przekształćmy dyskutowane równanie do postaci

Funkcja
posiada minimum
w punkcie
, gdyż

w pozostałych punktach jej wartości są większe od 1. Natomiast wartości funkcji
są zawsze niewiększe niż 1, przy czym
W konsekwencji jedynym rozwiązaniem naszego równania jest liczba
.

Jeżeli
, to postać kanoniczną funkcji kwadratowej można przekształcić do postaci iloczynowej:

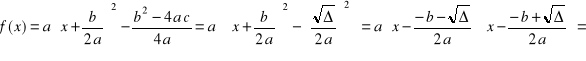
gdzie

W przypadku, gdy
postać iloczynowa ma kształt:

Dla
postać iloczynowa funkcji kwadratowej nie istnieje.

Przykład. Doprowadzimy ułamek

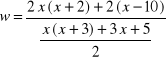
do najprostszej postaci.

Rozwiązanie. Mamy

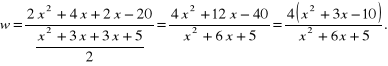
Aby skorzystać z podanych wyżej wzorów na rozkład trójmianu kwadratowego na czynniki, obliczmy wyróżniki: licznika
i mianownika
oraz wykonajmy stosowne obliczenia:

Stąd:

Konsekwencją postaci iloczynowej trójmianu kwadratowego jest następujące twierdzenie:

Niech
gdzie
oraz
będzie funkcją kwadratową. Wtedy

(i) jeżeli
to funkcja f nie ma miejsc zerowych;

(ii) jeżeli
to funkcja f ma jedno miejsce zerowe równe

(iii) jeżeli
to funkcja f ma dwa różne miejsca zerowe wyrażone wzorami:

Miejsca zerowe funkcji kwadratowej nazywamy pierwiastkami tej funkcji.

W uzupełnieniu poprzedniego twierdzenia, zanotujmy ważną własność:

Jeżeli
, to funkcja kwadratowa
przyjmuje:

(i) tylko wartości dodatnie, gdy

(ii) tylko wartości ujemne, gdy

Przykłady. Naszkicujemy wykresy trzech funkcji kwadratowych.

a)
.

Rozwiązanie.

b)
.

Rozwiązanie.

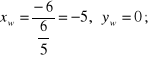
Ponieważ funkcja posiada tylko jedno miejsce zerowe, dla dokładniejszego naszkicowania wykresu funkcji obliczyliśmy wartości funkcji dla dwóch dodatkowych argumentów, wybraliśmy punkty symetryczne względem punktu
. Wykres ten wygląda następująco:

c)

Rozwiązanie. Postąpimy analogicznie, jak w poprzednim podpunkcie.

Przykład. Przedyskutujemy ilość rozwiązań równania
w zależności od wartości parametru c.

Rozwiązanie. Równanie można przekształcić do postaci

Ilość jego rozwiązań jest równa ilości punktów wspólnych wykresu funkcji
i funkcji stałej
Zauważamy, że

Funkcja f obcięta do przedziału
na dwa miejsca zerowe równe 0 i 2 oraz przyjmuje wartość najmniejszą równą
w punkcie
. Funkcja f jest funkcją nieparzystą, więc jej wykres
na przedziale
jest obrazem symetrycznym wykresu funkcji
w symetrii środkowej o środku
Kompletny rysunek wygląda więc następująco:

Stąd wynikają następujące wnioski:

• dla
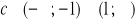
  równanie posiada jedno rozwiązanie;

• dla
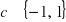
  równanie posiada 2 rozwiązania;

• dla
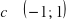
  równanie posiada 3 rozwiązania.

Wśród własności funkcji kwadratowej ważne miejsce zajmują tzw. wzory Viete'a. O naj­ważniejszych z nich mówi poniższe twierdzenie:

Liczby
i
są pierwiastkami funkcji kwadratowej
gdzie

i
wtedy i tylko wtedy, gdy spełnione są równości:

(i)

(ii)

Wzory Viete'a pozwalają na wyciąganie różnorodnych wniosków dotyczących trójmianu kwadratowego bez konieczności wyliczania jego pierwiastków, a nawet mogą być pomocne w szyb­kim odgadywaniu tychże pierwiastków. Ważnym zagadnieniem, w którym znajdują zastosowanie wzory Viete'a jest analiza znaków pierwiastków trójmianu kwadratowego.

Aby funkcja kwadratowa
posiadała dwa różne pierwiastki
,

(i) dodatnie potrzeba i wystarcza, by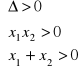
;

(ii) ujemne potrzeba i wystarcza, by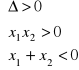
;

(iii) różnych znaków potrzeba i wystarcza, by
.

Przykład. Zbadamy, dla jakich wartości parametru k równanie

posiada pierwiastek należący do przedziału

Rozwiązanie. Mamy

Zauważmy, że

Dla
otrzymujemy równanie
którego jedynym pierwiastkiem jest liczba
nie należąca do przedziału
Analogicznie dla
powstaje równanie
o pierwiastku 1 spoza przedziału
Zakładajmy dalej, że
Zauważamy, że

skąd
oraz
Zatem, jeżeli
to
i odwrotnie. W konsekwencji rozważane równanie posiada pierwiastek w przedziale
wtedy, gdy posiada ono dwa pierwiastki ujemne. Wówczas jeden z tych pierwiastków należy do przedziału
a drugi do przedziału
(pierwiastki są różne, bo
Na mocy ostatniej własności równanie posiada dwa pierwiastki ujemne wtedy i tylko wtedy, gdy

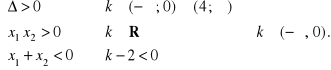
Rozwiązaniem równania kwadratowego
jest każde miejsce zerowe funkcji kwadratowej
Wiele równań innych typów daje się doprowadzić do równania kwadratowego przy pomocy różnych podstawień. Do takich równań należą tzw. równania dwukwadratowe:
gdzie

Przykład. Rozwiążemy wybrane równania sprowadzając je poprzez stosowne podstawienia do równań kwadratowych.

a)

Rozwiązanie. Podstawiając
otrzymujemy równanie kwadratowe

Ze wzorów Viete'a wynika, że jego pierwiastki
spełniają równości:
dzięki którym odgadujemy, że
Wracając do podstawienia, stwierdzamy, że
lub
. Stąd wnioskujemy, że równanie ma 4 rozwiązania:

b)

Rozwiązanie. Dziedziną tego równania jest zbiór
. Postawiamy
wówczas
czyli
. Rozwiązywane równanie przyjmuje postać

.

Stosując wzory Viete'a, odgadujemy pierwiastki:
. Stąd
lub
. Pierwsze z tych równań jest sprzeczne, a drugie posiada rozwiązanie
, które należy do dziedziny równania.

Nierównościami kwadratowymi nazywamy nierówności postaci:

Rozwiązujemy je najczęściej metodą graficzną szkicując schematycznie wykres odpowiedniej funkcji kwadratowej (przy pewnej wprawie wystarczy go sobie tylko wyobrazić).

Przykład. Rozwiążemy trzy nierówności.

a)
.

Rozwiązanie. Mamy

Pierwiastkami ostatniego trójmianu kwadratowego
są liczby:

Szkicujemy wykres funkcji f:

Widać, że zbiorem rozwiązań nierówności jest zbiór

b)

Rozwiązanie. Zauważamy, że

Uproszczony wykres wygląda więc następująco:

Zatem rozwiązaniami nierówności są liczby należące do zbioru
.

c)

Rozwiązanie. Ponieważ

więc
Stąd wykresem funkcji kwadratowej
jest parabola leżąca nad osią OX o ramionach skierowanych ku górze. W konsekwencji funkcja ta przyjmuje tylko wartości dodatnie i dlatego dyskutowana nierówność nie ma rozwiązań.

Często spotykanymi problemami dotyczącymi funkcji kwadratowej oraz równań kwadra­towych są zagadnienia z jednym lub większą liczbą parametrów. Oto kilka przykładów takich zadań.

Przykład. a) Przedyskutujemy liczbę rozwiązań równania

z niewiadomą x w zależności od wartości parametru m.

Rozwiązanie. Dla
mamy do czynienia z równaniem liniowym
które posiada jedno rozwiązanie.

Zakładajmy więc dalej, że
. Wówczas

gdzie
są pierwiastkami równania

Wiemy, że równanie kwadratowe ma dwa rozwiązania wtedy i tylko wtedy, gdy
. Mamy

Zatem

i dla takich m badane równanie posiada dwa pierwiastki.

Z poprzedniego rozumowania wynika, że

i wtedy rozpatrywane równie ma jeden pierwiastek (oraz dla
W pozostałych przypadkach, tj. dla
rozwiązań brak.

Uzyskane wyniki możemy przedstawić w czytelny sposób rysując wykres funkcji
która parametrowi m przyporządkowuje liczbę rozwiązań badanego równania.

b) Zbadamy, czy równanie

z niewiadomą x oraz parametrami
może posiadać 3 rozwiązania.

Rozwiązanie. Jeżeli
, to równanie staje się równaniem kwadratowym

które ma 0 lub 2 rozwiązania w zależności od tego, czy n jest liczbą parzystą, czy nieparzystą. Załóżmy więc, że
Mamy wtedy do czynienia z równaniem dwukwadratowym, które rozwiązujemy przez podstawienie
. Daje to równanie kwadratowe

Aby równanie dwukwadratowe posiadało trzy rozwiązania, odpowiednie równanie kwadratowe musi posiadać jedno rozwiązanie dodatnie i jedno równe 0. Czyli musi być spełniony układ warunków:

Mamy

Podstawiając
do ostatniej nierówności, otrzymujemy

tzn. n musi być dowolną liczbą parzystą.

Reasumując, dane równanie dwukwadratowe ma 3 rozwiązania wtedy i tylko wtedy, gdy
oraz n jest jakąkolwiek liczbą parzystą.

c) Zbadamy dla jakich wartości parametru a nierówność

jest spełniona dla każdego

Rozwiązanie. Zauważmy, że dla
otrzymujemy nierówność spełnioną dla wszystkich liczb rzeczywistych, a dla
nierówność, którego zbiorem rozwiązań jest przedział
Zatem
spełnia warunki zadania. Jeżeli
to mamy do czynienia z nierównością kwadratową, przy czym

Aby funkcja kwadratowa stojąca po lewej stronie nierówności była stale dodatnia wystarcza, aby

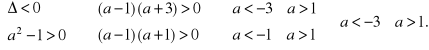
W konsekwencji, jeżeli
to wyjściowa nierówność jest spełniona dla wszystkich

d) Znajdziemy te wartości parametru a, dla których z prawdziwości nierówności

wynika prawdziwość nierówności

Rozwiązanie. Nierówność
jest prawdziwa dla
Pierwiastkami funkcji kwadratowej

są liczby
co łatwo wynika ze wzorów Viete'a lub wzorów na
i
A więc zbiorem rozwiązań nierówności
jest przedział otwarty o końcach a oraz
Aby ten przedział zawierał się w przedziale
musi być

.

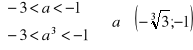
Zauważmy, że powyższe zadanie można także rozwiązać, korzystając z twierdzenia:

Niech
będzie funkcją kwadratową posiadającą dwa różne pierwiastki
oraz
będzie przedziałem skończonym w
Wówczas

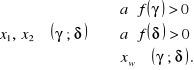
Ostatnim zagadnieniem, które poruszymy, jest kwestia rozwiązywania układów równań drugiego stopnia. Stosujemy tu podobne metody, jak w przypadku układów równań liniowych, choć niekiedy jest to trudniejsze i wymaga pewnej pomysłowości. Dla takich układów nie możemy stosować metody wyznacznikowej.

Przykłady. Rozwiążemy trzy układy równań.

a)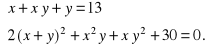

Rozwiązanie. Zauważamy, że

.

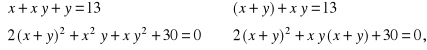
co sugeruje podstawienie:
Otrzymujemy układ równań

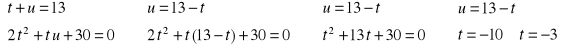
Wracając do niewiadomych x i y, otrzymujemy:

(1)

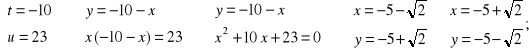
(2)

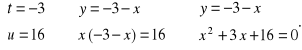
Układ (2) nie ma więc rozwiązań (wyróżnik równania kwadratowego jest ujemny) i dlatego rozwiązaniami wyjściowego układu są rozwiązania układu (1).

b)

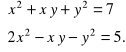
Rozwiązanie. Zastosujemy metodę przeciwnych współczynników:

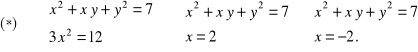
Dalej rozpatrzymy dwa przypadki.

1⁰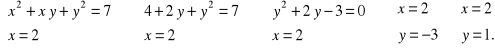

2⁰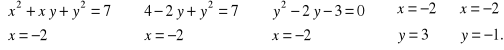

Stąd

c) (*)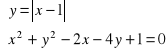
.

Rozwiązanie. Skorzystamy z metody graficznej. Zauważamy, że

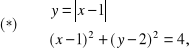
wobec czego należy naszkicować wykres funkcji
oraz okrąg o środku
i pro­mieniu 2:

Widzimy, że obie linie przecinają się w punktach o współrzędnych:
Stąd już łatwo sprawdzamy, że układ posiada trzy rozwiązania:

Rozdział 6. Funkcje kwadratowe 53

44

1

10

1

y

2

2

1

x

x

1



1

3

1

3

1

y

x

4

y

3

x

y

1

y

x

1

1

x

y

1

2

x

−1

m

1

1

−1

−1

15

−10

2

y

−2

---