PODSTAWY NIEZAWODNOŚCI

URZĄDZEŃ I SYSTEMÓW

Czas poprawnej pracy obiektu jest to czas od chwili rozpoczęcia pracy obiektu do jego uszkodzenia, oznaczony T.

Czas poprawnej pracy jest zmienna losową.

Rozkład czasu poprawnej pracy obiektu zależy od właściwości fizycznych obiektu i warunków jego eksploatacji.

Dystrybuanta czasu poprawnej pracy obiektu jest oznaczona F(t).

Funkcja gęstości czasu poprawnej pracy obiektu:

Postać ogólna zależności częstości uszkodzeń λ od czasu - tzw. krzywa „wannowa” (ang.: „bathtub hazard function”) jest przedstawiona na rys.

I II III

uszkodzenia uszkodzenia losowe uszkodzenia

niewykryte z powodu

w kontroli starzenia urządzenia

produkcyjnej (obiektu)

do długości tego etapu

powinien być dostosowany

okres gwarancji

Ogólna postać funkcji λ = f(t) odrębna dla każdego etapu I, II i III:

etap I: m < 0

etap II: m = 0

etap III: m > 0

1). Określenia, struktury niezawodnościowe

Niezawodność jest to prawdopodobieństwo pracy urządzenia bez uszkodzenia w założonym czasie i przy założonych warunkach narażeń (eksploatacji).

Symbol niezawodności: R (reliability) ( R < 1 )

Uszkadzalność (zawodność) jest to prawdopodobieństwo wystąpienia uszkodzenia urządzenia przed upływem założonego czasu pracy i w założonych warunkach narażeń (eksploatacji).

Symbol uszkadzalności (zawodności): F (failure) ( F < 1 )

R + F = 1

Struktury niezawodnościowe

1. Struktura niezawodnościowa szeregowa:

1, 2, ...... n - elementy struktury systemu

Uszkodzenie dowolnego elementu w tej strukturze powoduje uszkodzenie całego systemu.

Założenie: znana jest niezawodność elementu i-tego: Ri(t)

Jeśli analiza dotyczy etapu II „krzywej wannowej” częstości uszkodzeń w funkcji czasu, wówczas częstość uszkodzeń w tym etapie jest stała:

Wskutek występujących uszkodzeń następuje zmniejszanie się niezawodności elementu R_i(t) z upływem czasu eksploatacji według zależności:

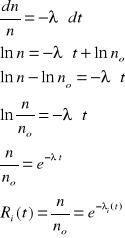
Niezawodność systemu o strukturze szeregowej wymaga, aby niezawodne były wszystkie jego elementy

Niezawodność systemu jest iloczynem logicznym niezawodności wszystkich elementów systemu.

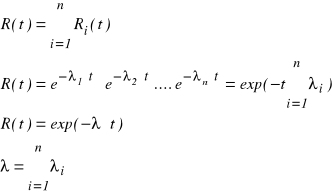
Średni czas do wystąpienia uszkodzenia (czas zdatności, trwałość, czas poprawnej pracy):

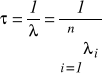
Jeżeli niezawodność elementu jest funkcją wykładniczą czasu, to niezawodność systemu o strukturze szeregowej jest również funkcją wykładniczą czasu.

2. Struktura niezawodnościowa równoległa

Struktura równoległa zachowuje poprawność pracy dopóki przynajmniej

jeden jej element pracuje niezawodnie.

Uszkadzalność systemu:

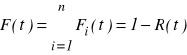
Uszkadzalność elementu w systemie:

(Ri(t) - niezawodność elementu w systemie)

Niezawodność systemu:

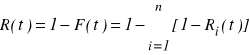
Jeśli:
(jak poprzednio, w strukturze szeregowej)

to niezawodność systemu jest:

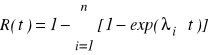
Jeśli niezawodność elementu jest funkcją wykładniczą czasu, to niezawodność systemu o strukturze równoległej nie jest już funkcją wykładnicza czasu. Średni czas do wystąpienia uszkodzenia nie jest odwrotnością częstości uszkodzenia, jak w strukturze szeregowej.

Ogólna postać wzoru na czas do uszkodzenia:

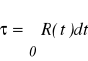
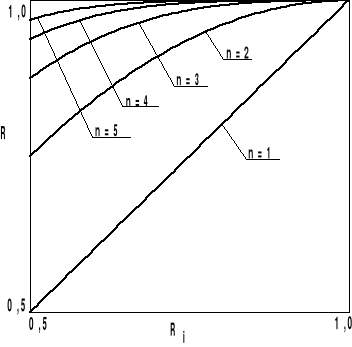
Jeśli częstość uszkodzeń elementów w strukturze równoległej jest jednakowa:

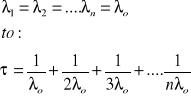
Zależność niezawodności R systemu o strukturze równoległej od niezawodności elementu w tej strukturze jest przedstawiona na rysunku:

3. Struktura niezawodnościowa szeregowo-równoległa

Podsystem 1 Podsystem 2 Podsystem k

System

Niezawodność systemu:

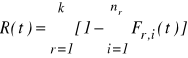
Fr,i(t) (i = 1,2...n) funkcja zawodności i-tego elementu w r-tym podsystemie

4. Struktura niezawodnościowa równoległo-szeregowa

Podsystem 1

Podsystem 2

Podsystem k

Uszkadzalność (zawodność) systemu:

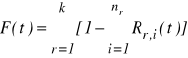
Niezawodność systemu:

5. Strukturaniezawodnościowa mostkowa

Niezawodność systemu:

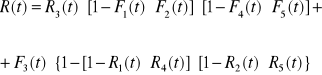
2). Podstawowe funkcje niezawodnościowe

Są to funkcje opisujące właściwości eksploatacyjne obiektów pod względem pewności spełniania przewidzianych dla nich zadań eksploatacyjnych

1. Niezawodność obiektu

R(t) = P(T ≥ t ) funkcja niezawodności

Opisuje prawdopodobieństwo, że czas zdatności T będzie nie mniejszy niż zadana wartość czasu t.

Ogólna postać przebiegu funkcji niezawodności w czasie (malejąca):

2. Zawodność obiektu

F(t) = P( T < t ) funkcja zawodności (ang.: failure)

Opisuje prawdopodobieństwo, że czas zdatności T będzie krótszy niż zadana wartość czasu t (wcześniej wystąpi uszkodzenie).

Czas zdatności lub trwałość lub czas poprawnej pracy obiektu jest zmienna losową, podlegającą określonemu rozkładowi statystycznemu.

F(t) = 1- R(t)

3. 
   Gęstość prawdopodobieństwa rozkładu czasu poprawnej pracy obiektu (zdatności)

Postać funkcji gęstości prawdopodobieństwa rozkładu czasu poprawnej pracy obiektu jest przedstawiona na rysunku:

Zależność pomiędzy funkcjami R(t) i f(t):

4. 
   Intensywność uszkodzeń

Krzywa „wannowa” intensywności uszkodzeń (rysunek)

Przykład:

Rozkład wykładniczy czasów zdatności do pracy:

• gęstość prawdopodobieństwa rozkładu czasu zdatności (poprawnej pracy):

• 
  funkcja niezawodności:

• intensywność uszkodzeń:

λ = const.

Uwaga: przypadek ten dotyczy II, (środkowego) etapu krzywej „wannowej” intensywności uszkodzeń.

• 
  oczekiwany czas zdatności:

Rozkłady prawdopodobieństwa czasu poprawnej pracy

1. Rozkład wykładniczy

a) Funkcja gęstości:

b - parametr skali, wartość jego zależy od jednostki czasu,

w której wyraża się czas poprawnej pracy T i czas bieżący t

b) Dystrybuanta:

c) Wartość oczekiwana czasu poprawnej pracy:

d) Funkcja intensywności uszkodzeń:

2. Rozkład Weibulla

• Prawdopodobieństwo pracy bez uszkodzenia (niezawodność) do chwili t jest w krzywej wannowej opisane funkcją:

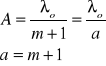
• Prawdopodobieństwo uszkodzenia (zawodność) w ciągu czasu od t = 0 do t, jako zdarzenie przeciwne do pracy bez uszkodzenia jest opisane funkcją dopełniająca do 1:

(1)

Wzór (1) jest dystrybuantą rozkładu Weibulla prawdopodobieństwa uszkodzenia urządzenia (obiektu).

Wielkości A i a są parametrami opisowymi rozkładu Weibulla

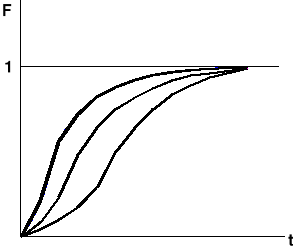
Postać graficzna dystrybuanty rozkładu Weibulla:

Linearyzacja rozkładu Weibulla: przekształcenie do postaci funkcji liniowej, łatwej do identyfikacji graficznej

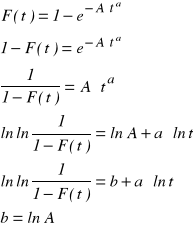
Skala odciętych:

Skala rzędnych:

Na podstawie linearyzacji rozkładu Weibulla opracowana jest siatka graficzna tego rozkładu .

Siatka służy do graficznej weryfikacji danych empirycznych.

Siatka rozkładu Weibulla

11

Niezawodność_12_13_2

1

2

n1

1

2

n

System

n

2

1

t

λo

λ

wpływ parametrów A i a

Wpływ a

Wpływ A

Y = const

(F(t) = const.)

Y

x

n2

2

1

nk

2

1

n1

1

2

1

nk

2

1

2

n2

1

4

2

5

3

R(t)

t

0

1

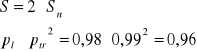
λ(t)

t

f(t)

t

λ

0

R(t)

t

1

0

λ(t)

t

λ

---