„KONSTRUKTYWIZM W EDUKACJI MAŁYCH DZIECI” (ZESZYT)
Wygotski w przeciwieństwie do Piageta nie wierzył, że dzieci mogą poznać świat samodzielnie, na własną rękę. Poznawanie, rozumienie świata przez dziecko możliwe jest tylko w kontekście społecznym, na współpracy z innymi ludźmi. Źródła rozwoju poznawczego tkwią zatem we wzajemnych interakcjach z osobami bardziej kompetentnymi, posiadającymi większą wiedzę. Dzięki interakcjom z dorosłymi w środowisku społecznym uczeń ma możliwości obserwowania i naśladowania innych i w konsekwencji rozwija w sobie wyższe czynności umysłowe.
SAR - strefa aktualnego rozwoju (dziecko)
SNR - strefa najbliższego rozwoju (dorosły)
6 ZASAD KONSTRUKTYWIZMU (planowania sytuacji stanowiących wyzwanie dla aktualnego poziomu rozwoju dzieci):
tworzenie sytuacji edukacyjnych
sprzyjanie aktualizmowi, poszerzaniu i rekonstrukcji przez dzieci posiadanych zasobów wiedzy potocznej, konfrontowanie własnych teorii odnoszących się do rożnych obszarów rzeczywistości z wiedzą, teoriami innych uczestników sytuacji edukacyjnych
umożliwianie dzieciom angażowania się w proces analizowania i rozwiązywania ważnych problemów mieszczących się w różnych dziedzinach nauki, życia i funkcjonowania człowieka
tworzenie okazji do podejmowania przez dzieci działań badawczych, poszukujących nie tylko indywidualnie, ale i małych zespołach
występowanie nauczyciela w roli współuczestnika działań dziecięcych; obserwując dzieci, prowadząc z nimi rozmowy, dyskutując poznaje ich sposób myślenia i rozumowania, zasób wiedzy i umiejętności; dzięki temu może zaplanować takie sytuacje, które stanowią wyzwanie dla aktualnego poziomu rozwoju dzieci
tworzenie w grupie dziecięcej atmosfery współpracy, która jest wynikiem stanowienia egalitarnych stosunków opartych na współdziałaniu nauczyciela z uczniami
M.KIELAR - TURSKA
STYMULOWANIE → doskonalenie, wspieranie rozwoju (nie przyspieszanie); stwarzanie sytuacji edukacyjnych i zachęcanie dzieci do działań prowadzących do samorealizacji
(rozdział 1. w: „Jak pomagać dziecku w poznawaniu świata”)
Efekty przyspieszania są krótkotrwałe - przy takim efekcie dziecko nie do końca zrozumie sens a brak pełnego zrozumienia wywołuje odtwórczość, napięcia emocjonalne (presja otoczenia).
Kielar - Turska proponuje doskonalenie, wspieranie rozwoju. Ćwicząc orientację w przestrzeni np. rysujemy, wskazujemy kierunki. Proces może być rozłożony w czasie, powtarzalny.
3 FORMY AKTYWNOŚCI:
percepcyjna (graficzna)
ruchowa
słowna (słowna)
STRATEGIE AUTORKI KROK PO KROKU:
ZAARANŻOWANIE SYTUACJI PROBLEMOWEJ, w której dziecko może odkryć problem, próbuje go określić i proponuje rozmaite sposoby rozwiązań
WYWOŁANIE ZACIEKAWIENIA - nauczyciel zaciekawia i zachęca do poszukiwania wszystkich możliwych rozwiązań, służy pomocą w porządkowaniu wyników dziecięcych obserwacji i poszukiwań
EKSTRAPOLACJA przeniesienie opracowanego problemu na inne treści i sposoby działania dziecka; zdaniem nauczyciela jest śledzenie prób dziecka (np. zadawanie zaskakujących pytań typu: dlaczego nie można gotować zupy w czajniku?), udzielanie wyjaśnień, inicjowanie innych sposobów rozwiązania zadania, dzieci próbują rozwiązać nowe problemy i odkrywać powtarzalność rozwiązań
ZABAWA RUCHOWA (relaksacja, nauczyciel włącza elementy sytuacji problemowej do zabawy ruchowo - tematycznej, wiąże w ten sposób rozwiązywanie problemu z przeżyciami dzieci)
DZIECIĘCE EGZEMPLIFIKACJE OPRACOWYWANEGO PROBLEMU czyli własne przykłady dzieci w zakresie stawiania i rozwiązywania problemów (prace plastyczne, techniczne dzieci)
OCENA O CHARAKTERZE OPISOWYM (nie wartościującym) towarzyszy krokom postępowania nauczyciela z dziećmi, odbywa się w trakcie zajęć - komentarze dorosłego do tego co dziecko powiedziało, zrobiło
dobra znajomość dziecka
przygotowanie odpowiedzi, które dla dziecka są zrozumiałe
uświadomienie sobie celu działania, którym jest aktywność poznawcza
należy zorganizować przestrzeń dla pracy - ARANŻACJA WNETRZA:
WYZNACZNIKI MATERIALNE (widoczne) np. kącik do czytania, stolik z farbami - komunikat jeśli chcesz pomalować zrób to!
WYZNACZNIKI NIEMATERIALNE (niewidoczne) np. to że każda zabawka ma swoje miejsce i tam należy ją odkładać, to że bawimy się zgodnie, nie robimy nikomu krzywdy (pewne zasady)
Układ kołowy w sali jest bardzo dobry - zapewnia kontakt wzrokowy z każdym
BOŻENA MUCHACKA - STRATEGIA WSPIERANIA ROZWOJU DZIECKA
Dziecko bawiąc się przyswaja wiedzę rozwiązując zadania. Dziecko należy nie tylko zachęcać ale wyposażyć w NARZĘDZIA POZNANIA (mówił on nich Wygotski: świat poznajemy dzięki zmysłom, później analizujemy, zapamiętujemy) - to procesy poznawcze dzięki którym to, co dociera przez zmysły jest analizowane, utrzymywane, uogólniane, obserwacja.
Dzięki tej strategii: dzieci będą lepiej uogólniały, koncentrowały uwagę, obserwowały.
Powinna istnieć struktura zajęć, która będzie odbiciem wiedzy dziecka - proponowane OGNIWA ZAJĘĆ:
Działania nauczyciela dotyczące poznawania przez dziecko istoty, cech, miejsca, przyczyn, skutków i znaczenia zjawisk tworzą scenariusz zajęć, tworzących strukturę pojęcia w umyśle dziecka (np. pojęcia przyrodnicze).
ISTOTA: Co ci przychodzi do głowy gdy słyszysz słowo...?
CECHY: Do czego jest podobne... co ci przypomina?
PRZYCZYNY: Czy wiesz skąd się biorą..?
MIEJSCE: Gdzie można zobaczyć...?
CECHY: Czy wszystkie... są takie same?
ZNACZENIA: Czy... są potrzebne? Jak myślisz dlaczego?
STAŁOŚĆ: Czy... występują zawsze?
SYNONIM / ETYKIETA: A czy można nazwać... jakimś innym słowem?
ETAPY:
ARANŻOWNIE SYTUACJI EDUKACYJNEJ
odkrycie tematu / zaciekawienie; może mieć formę DIAGNOZY - nauczyciel diagnozuje wiedzę dziecka (Co dziecko wie o...? - istota, cechy); głownie zabawa
KONSTRUOWANIE I REKONSTRUKCJA WIEDZY
dostarczanie wiedzy przez różne zabawy, opowiadania, wiersze, wycieczki pełniące w tym wieku największą rolę - w których dziecko tworzy wiedzę, nauczyciel tylko ukierunkowuje, dziecko decyduje o formie aktywności w określonym czasie; stymulują: uwagę, pamięć, logiczne myślenie; dostarczanie wiedzy trybem zabawy - dzieci aktywnie zdobywają wiedzę (wycieczka, wiersz, opowiadanie);
celem zajęć jest wszechstronny rozwój w każdej sferze, porządkowanie, organizacja wiedzy, aplikacja (dostarczanie) i transfer wiedzy
EWALUACJA I INFORMACJE ZWROTNE
tu nauczyciel diagnozuje wiedzę dziecka po 2 etapie; pobudzane są takie sfery jak kreatywność, wyobraźnia - dzieci wykonują prace plastyczne, mogą przenosić wiedzę którą zdobyło na inne obszary-ekstrapolacja
GARDNER → inteligencja wieloraka; ta strategia ma dążyć nie tylko do stymulowania inteligencji matematycznej ale i pojęcia dotyczące kultury, świata, bezpieczeństwa, zdrowia; tworzenie MAP MENTALNYCH (pojęciowych) - ma je tworzyć nauczyciel o dziecku na 1 etapie
METODA PROJEKTÓW
Korzyścią tej metody jest to że może ona zainteresować rodziców i zachęcić ich do udziału w podejmowanych przez dzieci działaniach. Jest to istotne, bo sukcesy dziecka w nauce zależą w dużej mierze od stopnia zaangażowania rodziców w proces edukacji.
Epstein wyróżnia 6 RODZAJÓW AKTYWNOSCI RODZICIELSKIEJ, podczas realizacji projektu występują: wolontariat, nauka w domu, kontakt z domem, współpraca ze środowiskiem;
Gdy nauczyciel pokazuje dokumentację działań dziecka i opowiada czego się uczą rodzice są zachwyceni poziomem rozumowania swojego dziecka, zdarza się że rodzice zaczynają się interesować projektem tak dalece, że zabierają dzieci na wycieczki po zajęciach, kupują im książki związane z tematem, przynoszą potrzebne materiały. Często występują w roli EKSPERTÓW odpowiadających na pytania małych badaczy, mogą towarzyszyć grupie podczas wypraw terenowych. Zakończeniem projektu jest pokaz prac dziecięcych.
Zajęcia typu lekcyjnego |
Projekty |
-- nie sprzyjają przejawianiu inicjatywy przez dziecko czy podejmowania odpowiedzialności za wykonaną pracę; -- krótkotrwały wzrost umiejętności szkonych; |
-- pozwalają na kierowanie swoją aktywnością i rozwijanie zainteresowań; --sprzyjają krótko- i długotrwałemu rozwojowi um. szkolnych: -lepsze wyniki nauce pisania, czytania, liczenia; -wyższa średnia ogólna oraz z poszczególnych przedmiotów(zw. chłopcy); -- możliwość rozwijania zainteresowań oraz samodzielnego zgłębiania zagadnień; |
ZALETY METODY PROJEKTÓW:
dziecko koncentruje się na 1 temacie
łączy wiedzę z rożnych dziedzinach
wiedza zdobywana jest w sposób praktyczny
dziecko samo podejmuje działanie
metoda projektów uwzględnia podmiotowość dziecka (ma możliwość wyboru zadania, ma prawo szukać rozwiązań na własną rękę, ma prawo do własnego sposobu przedstawienia wyników badań)
dowiaduje się na czym polegają badania naukowe
podejmowanie czynności przedstawiających (zadania połączone z fantazjowaniem - drama, kalambury; rysunki z treścią; rozumienie symboli przestrzennych - fotografie, strzałki, modele)
METODA PROJEKTÓW UWZGLĘDNIA PODMIOTOWOŚC DZIECKA, BO:
-- ma możliwość wyboru zadania
-- ma prawo do szukania rozwiązań na własną rękę
-- m aprawo do własnego sposobu przedstawienia wyników badań
M. P. umożliwia podejmowanie czynności przedstawiających-zabawy połączone z fantazjowaniem, drama, rysunki z treścią, rozumienie symboli przestrzennych, np. fotografie, proste mapy, modele
ETAPY (struktura obejmuje 3 etapy, projekt trwa 2-3miesiące):
* WYBÓR TEMATU
pojawia się ewentualny temat (z inicjatywy n-la lub w wyniku zainteresowań dzieci);
przygotowanie puli możliwych tematów do wyboru (glosowanie)
ustalenie co wiemy na ten temat
przygotowanie siatki wstępnej z pytaniami, wymogami dydaktycznymi, materiałami (dzieci zadają pytania, n-l nie odpowiada, ale wspól
nie zbiera to, czego chcemy się dowiedzieć);
zajęcia wprowadzające i budowanie wspólnych doświadczeń dla całej grupy;
decyzja czy temat jest odpowiedni i możliwy do realizacji;
przygotowanie listy pytań przez n-la
* PLANOWANIE ZAJĘĆ TERENOWYCH; EKSPERCI
Skąd możemy się dowiedzieć: zajęcia terenowe, biblioteki, księgarnie, zoo, sklepy zoologiczne, las, weterynarz, gospodarstwo, wizyty „ekspertów”
analiza wstępnej siatki przygotowawczej i pytań w celu powiązania treści i umiejętności
przygotowanie zajęć teoretycznych i wizyt ekspertów
aktywność badawcza
przedstawienie zdobytej wiedzy:opisy, rysunki, działania konstrukcyjne, taniec, inscenizacja
* TWORZENIE DOKUMENTACJI
dyskusja podsumowująca
przygotowanie wydarzenia kulminacyjnego (np. albumu)
zakończenie wydarzeniem kulminacyjnym lub zajęciami kulminacyjnymi
analiza projektu i ocena realizacji celów
JAK WPŁYWA METODA PROJEKTÓW:
→ w zakresie umiejętności czytania i pisania: celowość-czytanie aby zdobyć informacje, tworzenie siatki pojęć, pisanie pytań i odpowiedzi, dekorowanie napisów, tworzenie rysunków i podpisów do nich, udawanie że notują
→ rozwiązywanie problemów: w sposób spontaniczny, gromadzenie informacji, ich przetwarzanie, klasyfikacja, stosowanie narzędzi badawczych; dzieci nie uzyskują gotowych odpowiedzi-uczą się same zdobywać wiedzę
→ w zakresie rozwoju emocjonalno - społecznego: nawiązywanie kontaktów z obcymi, przełamywanie barier, opanowywanie strategii negocjacji między sobą, pozytywna motywacja, odczuwanie przyjemności z podejmowanego wysiłku, swoboda inicjowania, poczucie bycia ekspertem
→ osiągnięcia szkolne: lepsze wyniki w nauce, wiedza o różnych sposobach poszukiwania wiedzy (brak poczucia bezradności); pokazuje dziecku , że są inne sposoby zdobywania informacji poza dorosłym
A. TWARDOWSKI „Komunikowanie się dorosłego z dzieckiem”
JĘZUK MACIERZYSTY = ukierunkowany na dziecko:
konkretne, niezróżnicowane słownictwo
brak błędów gramatycznych
wyższe natężenie głosu
wyrazisty akcent
przewaga wypowiedzi zorientowanych na tu i teraz
ukierunkowane na aktualne zainteresowania dziecka
Wykorzystywanie zainteresowania dziecka przedmiotami:
-- wskazywanie przedmiotu
-- nazywanie go
Rola mediów w rozwoju dziecka:
-- ograniczają bezpośrednie relacje międzyludzkie
Przejście od treści spostrzeżeniowych (aktualne) do wyobrażeniowych (analogie)
Dorosły uważnie słucha dziecko (komunikaty werbalne i niewerbalne):
-- stajemy na równi z partnerem-twarzą w twarz
-- nie z dużo mówić
-- akceptujący uśmiech
-- potakiwanie głową
--„rozumiem”, „hmm”, „mhm”, „niesamowite” itd.
4rodzaje próśb o wyjaśnienie:
1. OGÓLNE (proszę, co, jak, nie rozumiem…)
2. O POTWIERDZENIE WYPOWIEDZI (powtarzanie wypowiedzi)
3. O DODATKOWE INFORMACJE
4. O UZUPEŁNIENIE WYPOWIEDZI (kto, co, jak, kiedy)
Wywoływanie rozbudowanych wypowiedzi:
-- umiejętne zadawanie pytań
-- stymulowanie
-- dziecko musi czuć się kompetentne
Zachęcanie do zadawania pytań:
-- ukierunkowanie uwagi
-- zadawanie pytań
-- dostarczanie bodźców, stwarzanie sytuacji do zadawania pytań
Nauczanie okolicznościowe:
-- wykorzystywanie zadawania pytań
Elementy wypowiedzi stymulujące |
Elementy wypowiedzi hamujące |
|
|
K. KAMIŃSKA „Nauka czytania w wieku przedszkolnym”
MOTYWY(dlaczego dziecko zaczyna czytać) |
RODZICE (działania) |
SPOSÓB STYMULOWANIA |
*chęć poznawania świata (świat do dziecka zwraca się w sposób graficzny - bilbordy, plakaty), przepływ informacji odbywa się drogą znaków i symboli *ciekawość, zainteresowania *uniezależnienie od dorosłych - dziecko chce być taki jak starszy (rodzeństwo) *dorównanie dorosłym *odnajdywanie informacji *interakcje społeczne motywują *porozumiewanie się symbolami *wzrastające tempo życia (np. mama mówi w który bus wsiąść) |
*czytanie dziecku 20 minut dziennie *zapewnianie dostępu do materiałów czytelniczych *czytanie nie powinno być przymusem powodowanym dążeniem do zrobienia z dziecka geniusza osiągającego karierę (błędna motywacja że nauczyciel kazał); ważne jest aby dzieci czytały ze zrozumieniem i żeby wymagania były dostosowane do ich możliwości *obserwuje jak rodzice czytają dla siebie (pokazują, że to jest fajne) *nie należy tłumić zainteresowania dziecka czytaniem |
*stawianie dzieci w sytuacji komunikowania się przez znaki *zabawy I. Majchrzak „wizytówki” *nie stawianie ram wiekowych *podtrzymywanie spontanicznych prób *rozciągnięcie nauki czytania na kilka lat |
INNE METODY NAUKI CZYTANIA
(DOMAN, BOGDANOWICZ, MAJCHRZAK)
E. GRUSZCZYK - KOLCZYŃSKA „DZIECIĘCA MATEMATYKA” - program nauczania matematyki w przedszkolu
UCZENIE SIĘ MATEMATYKI W PRZEDSZKOLU
ETAP - OD PRZYJŚCIA DO PRZEDSZKOLA
*ćwiczymy rozumowanie operacyjne (operacje konkretne) - dziecko poznaje liczbę w 3 aspektach:
- kardynalnym (ile jest przedmiotów)
- porządkowym (ile razy dany przedmiot mieści się w innym)
- miarowym (który z kolei jest przedmiot)
*jak należy liczyć przedmioty - zachęcać dziecko do liczenia na palcach (intuicja 1 do 1 - gest wskazywania)
*ogólna sprawność percepcyjna, ruchowa, koordynacyjna dziecka
*odporność emocjonalna na sytuacje trudne (ćwiczona poprzez gry, w wieku 5 lat konstruowane samemu = uczenie się porażki)
ETAP - KSZTALTOWANIE UMIEJĘTNOŚCI MATEMATYCZNYCH (6 ROK ŻYCIA)
<, >, - , +; zadania tekstowe
E. Gruszczyk - Kolczyńska w swoim programie wymienia 12 obszarów umiejętności matematycznych, które dziecko powinno nabyć w przedszkolu:
ORINTACJA W PRZESTRZENI
Związana jest z przestrzenią: relacja między przedmiotami. Dziecko powoli zdobywa orientację w przestrzeni. Ujmuje przestrzeń wieloma zmysłami /w okresie prenatalnym/ Następnie dziecko poznaje przestrzeń:
- dotykiem
- słuchem
Zmysły te doskonalą się z czasem
- przedmioty nabierają w oczach dziecka cech stałości ok. 6 miesiąca życia dzięki manipulowaniu. Dziecko zaczyna się poruszać:
działa w obrębie ust
w zasięgu ręki
w zasięgu wzroku
w zasięgu nóżek
Twarz mamy jest pierwszym punktem odniesienia .
Najpierw pojawia się rozumienie przestrzeni w poziomie (przed, za)-raczkowanie,
Druga to przestrzeń pionowa (wyrzuca przedmioty z łóżeczka) - zabawy: przed, za, u góry, u dołu; dziecko boi się pochyłości.
Dziecko poruszając się zdobywa nowe punkty odniesienia: łóżeczko, stół
Po 2 r.ż. dziecko powinno odróżniać opozycje tutaj - tam, daleko - blisko, z przodu - z tyłu, u góry - na dole, w - z (człowiek najszybciej przyswaja nad, przed)
3 r.ż. dziecko jest w różnych miejscach (nie tylko w domu i zapamiętuje je ale nie potrafi ich znaleźć, nie potrafi narysować przestrzeni, opisać jej - w tym wieku powinno być bardzo dużo zabaw konstrukcyjnych (w, obok), oglądanie np. domku z góry = przestrzeń z lotu ptaka
dopiero 5 latek wyobraża sobie przestrzeń, ale ma trudności z rozróżnianiem prawo - lewo (obok # koło) - powiązanie że lewa strona jest tam gdzie wyczuwamy bicie serca - frotka na lewej ręce
Gruszczyk - Kolczyńska:
Orientacja w przestrzeni wokół ciała
Polem pracy dziecka jest dywanik - gładki, sztywny
Dziecko 2 letnie:
jesteś tutaj, rzuć woreczek tam, do przodu (pokazujemy), pokaż gdzie jest woreczek, pobiegnij po niego
jesteś tutaj rzuć woreczek za siebie, pokaż gdzie jest woreczek, przynieś
krzesło: połóż misia koło krzesła, przed krzesłem
Dziecko 6 letnie:
usiądź na krześle, spójrz za siebie, przed siebie, w lewo, w prawo;
wstań połóż misia pod krzesłem, za krzesłem
Wraz z wiekiem przechodzimy od orientacji w stosunku do siebie, do orientacji w stosunku do innych osób = DECENTRACJA:
(miś siedzi na krześle): jak myślisz czy misiu wie co jest za krzesłem?
Ćwiczenia w schemacie swojego ciała
pantomima
rysowanie człowieka
dorosły: narysuje ciebie, opowiadaj jaki jesteś a ja cię będę rysować, potem zamiana ról
rozwijanie zdolności obdarzania uwaga innej osoby - rysunek znanych osób pod dyktando, przypominamy o detalach
dorosły stoi na kartce i pyta: gdzie mam położyć woreczek? (celowo myli się żeby dziecko mogło sprawdzić czy dobrze zrobił)
„szukaj misia” - opis a dziecko szuka
pokaż brzeg góry kartki, dół, lewy brzeg, prawy brzeg,
klepnij prawy górny róg
kreślenie wzorów poczynając od kropki
RYTMICZNA ORGANIZACJA CZASU - RYTMY
przekładnie rytmów np. z układu / @ / @ - można go zapisać symbolami graficznymi, pokazać ruchem: klask, tup, klask, tup; pokazać słowem: ti ta ti ta
Dostrzeganie regularności w układach słuchowych, ruchowych, graficznych
zabawa w pociąg (klocki drewniane) - dorosły: zabawimy się w pociąg, klocek, klocek, klocek (min 3) teraz Ty układaj klocki dalej
teraz układamy na bal idą: misiu, lalka, misiu lalka (2 sekwencje)
sekwencje słuchowe (grzechotka, miska) - wystukiwanie rytmu i jego kontynuowanie
zamknij oczy: co to gra?
Zabawa w zegar (dźwięk i ruch): cyk cyk, bim bim, tik tak, bim bam bom
Uczymy się wyliczanek (np. raz dwa trzy laleczki szukasz ty - zaczynamy wyliczanie od siebie)
DZIECIĘCE LICZENIE
INTUICJA MATEMATYCZNA 1 DO 1 (każdej rzeczy odpowiada 1 element)
INTUICJA STAŁEJ KOLEJNOŚCI (liczebniki wymieniamy w stałej kolejności)
ZASADA LICZBY KARDYNALNEJ
ZASADA ABSTRAKCJI - INTUICJA GELMAN
ZASADA NIEWAZNOŚCI KOLEJNOŚCI
KLASYFIKOWANIE
w wieku 3 lat dziecko dokonuje prostej klasyfikacji (pokaż obrazki które do siebie pasują), ale np. subiektywnie oddziela krowę od zwierząt bo ma rogi i może zrobić krzywdę
w wieku 4 lat łączy obrazki w ZBIORY FIGURATYWNE tzn. tak układają przedmioty, żeby była między nimi zależność (np. talerz i łyżka, igła i nitka)
5 latek tworzy jakby ŁAŃCUSZEK OBIEKTÓW (dziewczynka, lalka, wózek, klocki, piłka bo dziewczynka wszystkim się bawiła
6 - 7 rok życia tworzy KOLEKCJE - korzysta z informacji językowych (wyrazy np. na „z”, owoce i wymienia je); gdy chodzi o obiekty i obrazki mówi: „bo to jest wszystko do mieszkania” (klasyfikacja ze wzgl na funkcję); klasyfikacja ze względu na kolor (6 latki) ALE tworzy tez kolekcje typu: dziewczynka i ubrania (to są ubrania dziewczynki) - pozostałości z łańcuszka obiektów, oraz bawi się kryteriami - zmienia je w trakcie klasyfikowania dodając obiekt i zmieniając kryterium
stosuje obiektywne i stałe kryteria
używa kilku kryteriów równocześnie
ustala relacje między częścią a całością - tworzy klasy (jest na etapie myślenia pojęciowego)
par identycznych (przedszkole)
par skojarzonych (dziewczynka i wózek)
łańcuszki skojarzeń (mini opowiadania)
kolekcje (rodziny wyrazów)
zabawa ruchowa „pokaż w jakiej jesteś grupie”: w tle muzyka, dzieci tańczą udając np. zwierzęta i samoloty, sala przedzielona jest na pół, gdy muzyka milknie mają pokazać do jakiej grupy należą
jw. ale podział na dziewczynki i chłopców lub wg propozycji dzieci (np. spódnice i spodnie) i każda grupa tańczy inaczej
zabawa w klasyfikowanie słów:
ćwiczenia percepcyjne (karty z pieskami w 3 desenie :), buda i piłka, każdy rodzaj pieska + buda, pies i piłka, pies czarny i piłka, pies łaciaty i piłka)
zabawa z guzikami (rożnej wielkości, kolorów, kształtu, o różnej ilości dziurek)
zabawa w nadawanie przesyłki (dziecko ma sklep z guzikami, N nadaje przesyłkę w kopercie oznaczenia / adresy „guziki duże 4-dziurkowe i czarne”;
o którym guziku myślę - nauczyciel stopniowo wymienia cechy guzika o którym myśli
zabawa percepcyjna „robimy albumy” - wybierz obrazki które do siebie pasują, dzieci przyklejają wybrane obrazki na kartki - tworzą książeczki podzielone na grupy np. o zimie, z literką A, o samochodach
GRY
na pierwszym piętrze mieści się kino
na drugim mieszkają dwa sympatyczne zajączki
na trzecim jest cukiernia, w której można kupić smakowite lody
na czwartym p. mieszkają dwa miłe misie
na piątym dwa kotki
na szóstym jest kwiaciarnia
na siódmym dwa zabawne pieski
na ósmym krasnoludki
Czy to jest dwa?
Za mało - wołają dzieci.
Jeżeli dwa jest za mało, to jeden także jest za mało. Zasłonię te liczby (przypina pasek papieru, którym zasłania cyfry 1 i 2). Czy to jest dwanaście?
Za dużo - odpowiadają dzieci.
Jeżeli dwanaście jest za dużo, to trzynaście, czternaście i piętnaście także jest za dużo. Zasłonię te cyfry.
ZAPISYWANIE CZYNNOŚCI MATEMATYCZNYCH
??????????????????????????????????
3 latki
4 latki
Drugi człowiek i jego otoczenie, czyli przyjmowanie punktu widzenia drugiej osoby - zestawy: z oknem, stolikiem i jabłkiem, staw z kaczkami (po 5 wersji) - opis obrazka, zgadnij, o którym obrazku myślę?
Wprowadzenie kierunku w przestrzeni np. od misia w prawo, w bok (5-6 latki),
DECENTRACJA - ustalanie stron ciała prawej i lewej (serce)
Rozpatrywanie otoczenia z punktu widzenia drugiej osoby
6 latki - orientowanie się na kartce papieru (poprzedzone marszem pod dyktando)
Czas jest trudniejszy dla dziecka niż przestrzeń, zrozumienie upływu czasu nie jest łatwe (dziecko boi się leżakować - kojarzy to ze snem całonocnym).
Rytmy regulują proces uczenia się świata przez człowieka, ponieważ człowiek uczy się tego, co powtarzalne - już w okresie płodowym dziecko wprowadza się w rytm, którym jest bicie serca matki.
Rejestrujemy: bicie serca, pory snu i czuwania, czynności pielęgnacyjne, huśtanie - uspokaja (regularność).
Spostrzegamy: regularny układ przedmiotów, rysy twarzy ładnej osoby, regularność mowy - zabawy słowne przy kąpieli typu „myju, myju”, „ciapu, ciapu”; a także „a ku ku”, „nie ma, nie ma, jest”; czytanie
Dziecko kiedy zaczyna mówić bawi się słowami np. wyliczanki (bardzo szybo uczy się słów).
Rozróżnia to jest mama, a to nie jest mama - to co jest podobne, a co nie. Przewiduje (np. wrócę po podwieczorku), wychwytuje regularności (wyklaskiwanie, wyliczanki - ćwiczenia przez pokaż).
3 latki:
4-5latki
* dostrzeganie rytmu
* sekwencja wzrokowa
* figury geometryczne
Intuicja jeden do jednego
- gest wskazywania pojawia się bardzo często u dzieci dziecko widzi że czegoś jest dużo a czegoś mało
- już 3 miesięczne dzieci zdają się zauważyć zmianę w liczebności obiektów
- 4/5 miesięczne odkrywają relację ilościową pomiędzy swoim działaniem a efektem (np. siłą potrząsania grzechotki)
- dzieci 2-3letnie rozumie „dużo”, „mało”, „jest”, „nie ma”
- dziecko 3 letnie zaczyna używać liczebników
ETAP 1. znajomość liczebników - występuje niezależnie od pojęcia liczby
ETAP 2. ustalanie równoliczności - myślenie w wieku przedszkolnym jest na etapie przedoperacyjnym
ETAP 3. dobieranie do pary - dziecko ustala równoliczność do pary
ETAP 4. uzasadnianie stałości ilości (dziecko traci pewność gdzie jest więcej wody gdy np. przelejemy tą samą ilość wody do innego pojemnika, gdy obrócimy kartki - obie z taką samą ilością kropek)
ETAP 5. dalsze doświadczenia w szeregowaniu i klasyfikowaniu
DEFINICJE:
TOŻSAMOŚĆ JAKOŚCIOWA - to wiedza, że jakościowa natura danej rzeczy nie zmienia się pomimo zmiany wyglądu
CENTRACJA - tendencja dziecięca która sprawia, że to, co jest oczywiste percepcyjnie najsilniej przyciąga uwagę i wprowadza dziecko w błąd; przejawem centracji jest pojęcie stałości ilości
EGOCENTRYZM DZIECIĘCY - tendencja do przyjmowania tylko jednej perspektywy (np. długości a nie ilości choć powinien ilości) - Piaget używał określenia SCENTROWANY
STAŁOŚĆ LICZBY - pojawia się w rozwoju wcześniej od pojęcia stałości masy; to wiedza, że iloscioe cechy obiektów są niezmienne
ĆWICZENIA:
* liczenie kasztanów razem z dzieckiem - 3latki - na konkretach np. kasztany, klocki
* dodawanie kasztanów przez doliczanie
* odejmowanie przez odsuwanie i przeliczanie
* 4 misie, 3 kasztany (polecamy dziecku rozdać misiom po 1 kasztanie), N: co możemy dalej zrobić?, popatrz misio, kasztan, misio, kasztan (rytmy)
* zabawa w sklep (żetony, rekwizyty np. klocki, zabawki) 1 pieniążek za jednego pluszaka, N: chcę kupić klocek i kładzie pieniążek na klocku
- układanie domków 4trójkąty i 4 kwadraty, N: dopasuj daszki domkom, policz ile jest trójkątów / kwadratów, ile jest domków
* zabawa w liczenie palców - N staje za dzieckiem, policz ile jest palców, dziecko liczy swoje i nauczyciela
zasada, która mówi, że ostatni wymieniony liczebnik ma 2 funkcje bo reprezentuje liczbę elementów;
dziecko nie ma tej intuicji ponieważ liczy od nowa cały czas; dopóki dziecko będzie widziało elementy to ma pokusę przeliczać, rada na to mogą być:
* czarodziejski worek (głośne przeliczanie przedmiotów i wrzucanie do worka; ile elem. wrzuciłeś?)
* magiczna skrzynka z odkrywaną pokrywką
Zabawy na konkretach prowadzimy bardzo długo np. kartka do kredki, filiżanka do spodka
PRZEDMIOTY ZASTĘPCZE:
a) żetony czyli figury Layla (3latki - 4 żetony)
- połóż tyle żetonów ile jest misiów
b) kostki rusieckiego (4/5latki - kartki z punktami)
- narysuj tyle kropek ile ile jest jabłek i gruszek , policz
* rolnik sam w dolinie (zabawa dla 4/5latków)
* Czego jest dużo, a co jest tylko jedno w świecie? (czego jest mało - trudność dla dzieci)
w taki sam sposób liczymy wszystko nawet niejednorodne przedmioty
np. dziecko liczy cukierki dowolnie ułożone
dziecko 5/6 letnie
* opisywanie relacji ilościowych na obrazkach (2 wersje z elementami: słońce, kwiaty, płotek, chmurki, ptak, kot) - dziecko wybiera 1, N: czego jest mało/dużo/najmniej/najwięcej/ tyle samo? Co jest jedno?
* opisywanie kolekcji (N przygotowuje różne zestawy, w pudelku powinny być elementy różnego rodzaju; N: wybierz pudełeczko, które ci się podoba, co w nim jest? Poukładaj elementy tak, żeby łatwo było ci opowiadać - dziecko ćwiczy wyodrębnianie podgrup; opowiedz)
KLASYFIKOWANIE jest zespołem czynności umysłowych, które pozwalają nam porządkować wiedzę o świecie; pełne klasyfikowanie operacyjne opanowywane jest ok 17 roku życia;
O klasyfikacji możemy mówić gdy dziecko zaczyna dostrzegać podobieństwo między przedmiotami
* 3 - 4 latki klasyfikują naraz wg jednej cechy
* 6 - 7 latki klasyfikują obiekty nawet wg 3 cech naraz ale trudność sprawia argumentacja
O umiejętności klasyfikowania operacyjnego świadczy, to że dziecko:
ETAPY:
Rozwijaniu klasyfikowania operacyjnego służą KARTY (8x8cm) z obiektami - umieszczonymi centralnie, odpowiedniej wielkości, jednoznaczne, w rożnych kategoriach (5 kategorii po 4 karty).
ĆWICZENIA w klasyfikowaniu:
dla najmłodszych:
* nauczyciel czyta wyliczankę a dzieci mówią np. ze była o zwierzątkach
* na wsi u dziadziusia koń jest? jest; świnka jest? jest; lew jest? nie ma (na parkingu u taty... etc)
* jedzie pociąg z owocami / butami... ma wagony z jabłkami, bananami/ klapkami, sandałami (dla starszych dzieci)
* podziel pieski ze względu na kolor
* pokaz pieski, które stoją przy budzie, a które przy piłce
* a teraz zabawimy się w szukanie pieska: znajdź pieski które są łaciate / czarne (potem zamiana ról)
* zabawa „o jakim piesku myślę” (opis a dziecko wybiera)
* co my zrobimy z nimi? jak je podzielić? (duże i małe), tworzymy domki (miseczki) ale domki nie mają adresów, propozycje dziecka jak oznaczyć, wykonanie oznaczeń i podpisanie nimi domków
* jak jeszcze możemy je podzielić?
Konstruowanie gier matematycznych z grupą dzieci w przedszkolu lub klasie zerowej.
Proponowany cykl zajęć zawiera cztery scenariusze zajęć mających na celu: liczenie przez dziecko w możliwie szerokim zakresie, gromadzenie doświadczeń sprzyjających rozumieniu aspektu porządkowego liczby naturalnej, zapoznawanie się z właściwościami dziesiątkowego układu pozycyjnego. Zajęcia są ułożone w taki sposób by powoli wzrastał poziom trudności Przechodzi się w zadaniach od treści bardziej opisowych, zawierających elementy fabuły do treści coraz bardziej konkretnych oraz od działań manipulacyjnych po działania symulacyjne. Wszystkie użyte cyfry powinny być zgodne z przyjętym wzorem. Gry przeznaczone są dla dzieci w starszym wieku przedszkolnym pięciolatków lub w klasie zerowej- sześciolatków, a nawet dla uczniów które rozpoczęły już naukę szkolną.
Pierwsze zajęcia z cyklu - „Jeździmy windą w zaczarowanym domu”
1.Nauczyciel (inna osoba dorosła) wywiesza na tablicy karton papieru na którym rysuje dom-blok, w którym jest dużo pięter, rysuje piętra oraz liczy je wspólnie z dziećmi. Rysuje również miejsce na windę na każdym piętrze oraz przykłada pudełko zapałek które jest windą i może umocować je na którymkolwiek piętrze np. za pomocą magnezu. Numeruje piętra(nie pomijając parteru, które w późniejszej fazie zabawy dzieci same mogą określić znakiem 0 ).
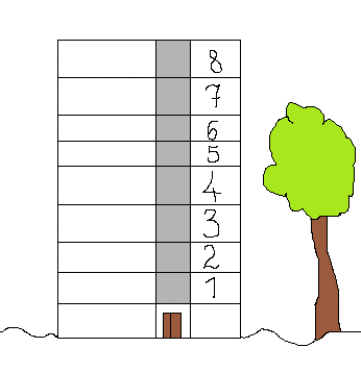
Opowiada dzieciom historię na temat zaczarowanego domu:
Nauczyciel przykleja jednocześnie sylwetki zwierząt lub inne oznakowania wspominanych elementów.
2.Rozpoczyna się zabawa, nauczyciel pyta różnych dzieci na które piętro chciałyby wyjechać, a sam jest windziarzem i przesuwa pudełko zapałek.
3.Następnie dzieci dostają potrzebne materiały i w dójkach tworzą na kartonie swój zaczarowany dom, za windę może posłużyć klocek, mogą same namalować zwierzęta lub użyć figurki zwierzątek.
4.Po wykonaniu planszy dzieci bawią się tak, że jedno jest windziarzem, drugie składa wizyty lokatorom - z zamianą ról. Jest to okazja do posługiwania się liczebnikami porządkowymi.
Drugie zajęcia z cyklu.
Każda bawiąca się para otrzymuje po jednej miarce krawieckiej i po jednym spinaczu do bielizny. Nauczyciel przypomina zabawę w zaczarowany dom, mówi, że w obecnej zabawie taśma krawiecka to nasz dom, który ma sto pięćdziesiąt pięter, a spinacz to winda. Dzieci bawią się analogicznie. Wybierają sobie na taśmie miejsce i przepinają spinacz. Nauczyciel podchodzi do każdej pary wyjaśnia, pomaga, pyta i słucha odpowiedzi. Jeśli by się dzieci zapytać skąd znają wybraną liczbę zazwyczaj kojarzą ją np. z numeru autobusu, mieszkania itp.
Można liczyć głośno pietra po których przesuwa się winda. Dzieciom zapewne będą się mylić liczebniki, dorosły powinien im podpowiadać. Może utrudnić grę np. zaczarować windę tak, że zatrzymuje się tylko tam gdzie jest zero lub jakaś inna wybrana liczba.
Dzieci dzięki tej zabawie zapoznają się z uporządkowanym szeregiem liczbowym i odszukują znane im liczby. Poznają miejsce gdzie się one znajdują, co jest przed każda z tych liczb, a co jest za nią. Osłuchują się także z liczebnikami i same próbują liczyć miejsca na taśmie, obserwując przy tym zapisane liczebniki.
Trzecie zajęcia z cyklu - „Polowanie na tygrysa”
Nauczyciel przygotowuje chodniczek liczbowy, zawierający kieszonki podpisane cyframi oznaczającymi liczby od 1 do 15 oraz liczmany odpowiadające tym samym cyfrom w odpowiedniej ilości.
Na początku dzieci dobierają symbole liczb na liczmanach odpowiednio do symboli na kieszonkach chodniczka oraz pokazują na palcach ile to jest. Nauczyciel odwraca się wybrane dziecko znajduje sobie pośród liczmanów liczbę która będzie tygrysem, pokazuje ją reszcie dzieci i chowa w kieszonce na chodniczku. Nauczyciel odwraca się i próbuje odnaleźć tygrysa. Jeżeli podana przez niego liczba jest mniejsza od tygrysa dzieci odpowiadają „za mało”, jeśli większa - „za dużo”, gdy zgadnie „trafiony”.
Np.
Nauczyciel wskazuje niezasłonięte pola i stwierdza, że tygrys musiał schować się pod jedną z tych kieszonek i pyta dalej, zasłania kolejne liczby aż trafi w odpowiednią. Rozgrywa jeszcze kilka polowań, po czym dzieci mogą zrobić swój chodniczek i grać w parach.
Czwarte zajęcia z cyklu.
Odbywają się analogicznie, tylko zamiast wybierać liczbę z liczmanów dziecko samo wpisuje ją na karteczce a nauczyciel odszukuje liczby na metrze krawieckim zawężając krąg poszukiwań dwoma spinaczami. Po paru rundach wspólnej gry dzieci mogą bawić się parami, również zapisują sobie liczby na karteczkach, żeby się nie pomylić ani nie zapomnieć.
Jest to zadanie trudniejsze od pozostałych, organizuje się je z dziećmi które mają niedługo rozpocząć naukę w szkole lub które już chodzą do szkoły.
Proponowaną serię zabaw i gier można zrealizować również w czasie zajęć indywidualnych lub z dwojgiem dzieci.
Gry-ściganki i gry-opowiadania
Wprowadzanie gier ściganek możemy podzielić na dwa etapy:
- pierwszy to konstruowanie gry-ściganki, w którym dzieci poznają sens gry tego typu - gra dla satysfakcji zwycięstwa, przestrzeganie określonych reguł. Po przeprowadzeniu takich gier przechodzimy do następnego etapu:
- konstruowania z dzieckiem gry-opowiadania.
Dorosły siada z dzieckiem przy arkuszu papieru. Wyjaśnia dziecku, co będą robić. Rysuje linie będące chodniczkiem, po którym poruszać się będą pionki. Wyglądać to może tak:
Konstruowanie gry-opowiadania
„Dwa niedźwiadki ścigają się, który z nich pierwszy dobiegnie do dzbanka miodu”.
Do skonstruowania i przeprowadzenia gry potrzebne będą następujące przedmioty: arkusze papieru (dla dwojga dzieci i dorosłego), taśma, kredki lub mazaki, klocki do odmierzania chodniczka (po jednym dla pary dzieci), dwie pinezki-pionki, figurki różnych zwierząt (po kilka dla pary), sylwetki z papieru - dwa niedźwiadki, wiewiórka, dzbanek, wilk oraz kostki do gry.
Na tablicy prowadzący przypina arkusz papieru. Rozpoczyna konstruowanie gry. Zwraca się do dzieci:
- Ułożymy nową grę. Narysuję chodniczek. Ewa pomoże mi odmierzyć płytki, a wy je głośno policzycie.
Dziecko za pomocą klocka odmierza odległość, dorosły rysuje płytki chodniczka. Wszystkie dzieci głośno liczą płytki, dorosły razem z nimi, aby się nie pomyliły. Po narysowaniu chodniczka dorosły przedstawia scenariusz gry, przypinając do arkusza kolejno sylwetki misiów i pojawiające się podczas opowiadania scenariusza przedmioty.
- Będą się ścigać dwa niedźwiadki. Biegną do dzbanka pełnego miodu. Miód to prawdziwy przysmak i dlatego niedźwiadki ścigają się: kto pierwszy dobiegnie, będzie miał więcej miodu.
Droga do dzbanka miodu biegnie przez zagajnik, łąkę, lasek. Dużo może się zdarzyć. Różne przygody mogą przeżyć nasze niedźwiadki.
Dorosły rysuje na planszy różne przeszkody, urozmaicające grę: - O, tutaj płynie strumyczek, a woda zmyła kładkę. - rysujemy wodę zakrywającą płytkę. - Niedźwiadki nie potrafią pływać, więc szukają innej drogi. - rysuje kawałek chodnika, którym można obejść mostek.
Pojawiają się również inne przeszkody - np. jama lisa, przy której rysujemy dodatkową pętlę chodniczka, aby ją obejść, lub zaznaczoną kolorem płytkę, dzięki której niedźwiadki przeskoczą jamę (dzieci muszą wyrzucić np. określoną liczbę oczek na kostce - 4 lub więcej). Inną przeszkodą mogą być kwiatki, przy których zatrzymuje się miś i wąchając je, traci jedną kolejkę. Możemy również zaznaczyć poziomki, dzięki którym miś nabiera siły i rzuca kostką dwa razy. Ostatnią przeszkodą, którą spotykają niedźwiadki, jest wiewiórka-psotnica, która wskazuje niewłaściwą drogę niedźwiadkom, przez co idą do celu naokoło.
Po narysowaniu planszy dorosły stwierdza, że jest gotowa, i rozpoczyna grę. Dzieli grupę na dwa zespoły, wybiera przedstawicieli. Przypina obok sylwetek niedźwiadków pionek. Przedstawiciele losują kolejność rzutów kostką. Każdy zespół dostaje kostkę. Dzieci kolejno rzucają kostką i liczą kropki. Ich liczbę podają przedstawicielowi, który na planszy przesuwa pionek. Gra się rozpoczyna.
Gra budzi w dzieciach emocje, rywalizację. Po skończonej grze zwycięzcy cieszą się, natomiast dorosły proponuje, aby drugi niedźwiadek szybko również dobiegł do mety, i w ten sposób oba zespoły są już na mecie.
Następnie prowadzący proponuje dzieciom samodzielne skonstruowanie gry. Na stolikach są zgromadzone wszystkie potrzebne przedmioty: arkusze papieru, klocki, kredki, figurki zwierząt, kostki.
Dzieci dobierają się parami. Odbierają od dorosłego arkusz, siadają na podłodze i konstruują grę.
Dorosły powinien zadbać o odpowiednie dobranie w pary tak, aby były to dzieci o podobnych możliwościach, aby mogły pracować na zasadzie partnerstwa, bez dominacji jednego z nich. Podczas konstruowania gier dorosły przygląda się pracy dzieci, wypytuje i podziwia. Pod koniec zajęć wypytuje o grę i wyniki. Po zakończonych zajęciach dzieci sprzątają.
Przy każdej grze-opowiadaniu dzieci konstruują nowe plansze, mogą zabrać je do domu i pokazać rodzicom.
Po kilku takich grach dzieci wykazują coraz więcej pomysłowości w wymyślaniu nowych wariantów, przeszkód, są bardziej twórcze.
Konstruowanie gier o rozbudowanym wątku matematycznym
Możemy zacząć wprowadzać je gdy słabnie u dzieci fascynacja grami-opowiadaniami, pamiętając jednak, że zmiana gier musi nastąpić łagodnie, aby nie zniechęcić dzieci nadmiernym wzrostem trudności.
Na początku tego etapu nowa gra powinna posiadać jeszcze otoczkę beletrystyczną ale z czasem będzie ona ustępowała miejsca czynnościom i operacjom matematycznym.
Tak jak to dzieje się w przypadku wszystkich gier na początku dorosły będzie osobą wiodącą i razem
z dzieckiem będzie konstruował nową grę rozgrywaną na zasadzie partnerstwa. Dopiero później samo dziecko będzie postacią wiodącą, tworzącą wariant poznanej wcześniej gry i zapraszającą dorosłego do rozgrywki.
„Zbieramy owoce w sadzie” to pierwsza gra z cyklu gier o rozbudowanym wątku matematycznym z jaką możemy zapoznać dzieci.
Potrzebne przedmioty:
- arkusz papieru
- pisaki lub kredki
- klocek do odmierzania płytek chodnika
- kostka do gry, dwa pionki
- dwa małe pojemniki
- więcej niż 50 żetonów (przedmioty zastępujące owoce, mogą to być kamyki, guziki, ziarna fasoli)
Pierwsze zajęcia z cyklu
Dorosły rozkłada na stole przedmioty potrzebne do budowania gry i zaprasza dziecko do wspólnej zabawy. Nauczę Cię nowej gry. Nazwałem ją Zbieramy owoce w sadzie. Tu jest brama - wejście do sadu, a tam wyjście. W moim sadzie jest chodniczek. Pomórz mi odmierzyć płytki. Po dwóch stronach chodniczka rosną drzewa owocowe.(rys.1)
Następnie dorosły mówi: Jeszcze tylko owoce. Mogą być nimi te fasolki. Umieśćmy je na drzewach po kilka - i wraz z dzieckiem układa fasolki w pętlach (rys.2)
Przebieg gry jest następujący:
- Mamy po koszyku na owoce (pojemniki)
- Ustawiamy pionki przy wejściu do sadu w narysowanych kółkach
- Losujemy, żeby ustalić kto rozpocznie grę
- Rzucamy przemiennie kostką i przesuwamy pionki po chodniczku
- Jeżeli pionek zatrzyma się pod drzewem, można zebrać owoce
- Wyga ten, kto zbierze więcej owoców
W tej grze należy zabrać jak najwięcej owoców. Szansa na sukces wzrasta, jeżeli grający wyrzuci mało oczek na kostce. W lepszej sytuacji jest ten kto zaczyna bowiem pierwszy może znaleźć się przy drzewach.
Po zakończeniu gry następuje liczenie punktów.
Jeżeli dziecko ma słabo opanowaną umiejętność liczenia sugerujemy aby ustawiło punkty swoje i dorosłego w rzędach i policzyło je - dorosły podpowiada liczebniki. Następnie dorosły mówi np.: Ty masz piętnaście, a ja trzynaście. Kto ma więcej? Kto wygrał?
Jeśli dziecko nie wie od razu jaka jest odpowiedź dorosły może wskazać na rzędy i zasugerować : To są twoje, a te moje. Porównamy je: jeden Twój, jeden mój - tak aby tworzyły pary. Co widzisz?
Gdyby i po tym liczeniu dziecko nie wiedziało kto ma więcej i o ile możemy oddzielić kredką lub pisakiem tą samą liczbę punktów tak, aby została tylko nadwyżka.
Drugie zajęcia z cyklu
Można przeprowadzić jeszcze tego samego dnia lub na drugi dzień
Trzecie zajęcia cyklu
Po dwóch trzech dniach dorosły proponuje dziecku grę. Rozkłada papier i wszystkie potrzebne przedmioty i mówi: Spróbuj zbudować grę podobną do tej, w którą graliśmy poprzednio. Zazwyczaj dziecko też narysuje sad. To dobrze. Możemy jednak pobudzić jego wyobraźnię sugerując, że można zbierać co innego.
(tego nie przerabialiśmy i nikt nie miał zadane do opracowania)
6
START
META
Rys. 1
Rys. 2
Wyszukiwarka
Podobne podstrony:
8453
8453
8453
8453
więcej podobnych podstron