Moment bezwładności-iloczyn masy cząstki przez kwadrat jej odległości od osi obrotu nazywamy momentem bezwładności cząstki. Możemy powiedzieć że dwie cząstki są równoważne ze względu na obrót dookoła osi gdy ich momenty bezwładności są równe. I=mr² Jeżeli wokół wspólnej osi porusza się układ n cząstek o masach m₁,m₂,...m_n znajdujących się odpowiednio w odległościach r₁,r₂,...r_n od osi to moment bezwładności całego układu nazywamy sumę momentów bezwładności poszczególnych cząstek I=Σm_ir_i² Dla całego układu rozkładu masy w ciele sztywnym moment bezwładności definiowany jest wzorem całkowym: I=_V∫ρr²dV ρ-funkcja opisująca gęstość ciała; V-obiętość ciała; dV-element objętości; r-odłegłość elementu dV od osi

Twierdzenie Steinera: moment bezwładności I ciała sztywnego względem dowolnej osi obrotu SS równa się momentowi bezwładności tego ciała I₀ względem osi równoległej do poprzedniej przechodzącej przez środek masy tego ciała plus iloczyn masy ciała M przez kwadrat wzajemnej odległości d obu osi: I=I₀+Md² Twierdzenie to pozwala określić jak zmienia się moment bezwładności przy przemieszczeniu równoległym osi obrotu.

P-płaszczyzna; SS,OO-osie; d-wzajemna odległość obu osi;

Najstalszą osią obrotu jest oś względem której moment bezwładności ciała jest największy. Przy wszelkiego rodzaju szybko wirujących częściach maszyn jak wirniki w maszynach elektrycznych, prądnicach, turbinach parowych i innych, bardzo ważną jest rzeczą, aby ich osie obrotu schodziły się jak najdokładniej z jedną ze stałych osi obrotu. W przeciwnym razie niezrównoważone siły odśrodkowe powodują drgania które mogą szybko zniszczyć łożyska i całą maszynę.

Ruchy-linię, jaką zakreśla punkt podczas ruchu nazywamy jego torem, a długość zakreślonego toru-drogą przebytą przez pkt. Drogę będziemy zwykle oznaczać literą S.

Ruch prostoliniowy jednostajny:Droga w ruchu jednostajnym jest funkcją liniową czasu. S=Vt Ruchem jednostajnym nazywamy ruch, w którym w równych czasach przebywane są równe drogi, ale tylko wtedy gdy dodamy zastrzeżenie, że te równe przedziały czasu mogą być dowolnie wybrane. Ruch niejednostajny. Prędkość i przyspieszenie w dowolnym ruchu prostoliniowym. Gdy droga przebyta przez pkt nie jest funkcją liniową czasu, ruch jest niejednostajny. Prędkość średnia-nazywamy stosunek przyrostu drogi do przyrostu czasu. V_Śr=ΔS/Δt Miarą prędkości chwilowej albo wprost prędkością ruchu zmiennego nazywamy granicę do której dąży stosunek przyrostu drogi do przyrostu czasu, gdy przyrost czasu dąży do zera V=limΔS/Δt

^Δt-0

Miarą prędkości ruchu zmiennego jest pochodna drogi względem czasu: V=dS/dt Gdy prędkość ruchu wzrasta z czasem ruch nazywamy przyspieszonym, gdy prędkość maleje-opóźnionym. Przyspieszenie średnie: a_Śr=ΔV/Δt Przyspieszeniem chwilowym nazywamy granicę do której dąży ten stosunek gdy chwile obserwacji zbliżają się do siebie nieograniczenie: a=limΔV/Δt=dV/dt

^Δt-0

Ruch jednostajnie przyspieszony bez V₀: S=at²/2; V=at; a=const.

z V₀: S=V₀t+at²/2; V=V₀+at;

Zasady termodynamiki-Każde ciało dzięki ruchom molekuł, z których jest złożone, ma pewien zapas energii kinetycznej, dzięki zaś siłom działającym między molekułami-pewien zapas energii potencjalnej. Suma tych energii stanowi tzw energię wewnętrzną ciała U.

I zasada termodynamiki:Przyrost energii wewnętrznej musi się równać sumie pobranej pracy i pobranego ciepła:

W+Q=U₂-U₁

ΔW+ΔQ=ΔU

Proces przekazywania energii z jednego układu ciał w wyniku różnicy temperatur nazywa się ciepłem Q.

Przemiana izotermiczna:Przy izotermicznych zmianach objętości gazu praca sił zewnętrznych zamienia się w całości na ciepło lub odwrotnie, pobrane ciepło zamienia się w całości na pracę, którą gaz wydaje rozprężając się przy pokonywaniu sił zewnętrznych.

W=-Q Sprężanie izotermiczne: W>0;Q<0

Rozprężanie izotermiczne: W<0;Q>0

Przemiana izohoryczna:Gaz nie wykonuje pracy W=0; ΔU=ΔQ

Z pierwszej zasady termodynamiki wynika perpetum mobile pierwszego rodzaju: silnik, który wytwarza pracę nie pobierając energii z zewnątrz.

II zasada termodynamiki:Ciepło może być zamienione na pracę tylko wtedy, jeżeli istnieje różnica temperatur ciał wymieniających ciepło, czyli gdy przechodzi ona z ciała o temperaturze wyższej(źródło ciepła) do ciała o temperaturze niższej(chłodnicy). Nie cała ilość pobranego ciepła może być zamieniona na pracę, bowiem część jego zostaje przekazana chłodnicy. Wnioski: -nie można zbudować silnika o sprawności η=100%

• Carnot wymyśli silnik doskonały, który ma sprawność największą przy danej różnicy temperatur. Jeżeli przekroczymy jego sprawność to możemy mówić o perpetum mobile drugiego rodzaju.

Rysunek 1:perpetum mobile drugiego rodzaju:η>η_c

Ryc.2:silnik Carnota:η_c=(T₂-T₁)/T₁

Ryc.3:silnik rzeczywisty:η<η_c

Cykl Carnota-

1.Rozprężanie izotermiczne:gaz wydaje pracę W₁ równoważną pobranemu ciepłu Q₁.

W₁=-Q₁ U=const.

V₂>V₁ dlatego ln(V₁/V₂) ma wartość ujemną z tąd praca W₁ jest ujemna czyli wydana, a ciepło Q₁-dodatnie czyli pobrane.

2.Rozprężanie adiabatyczne:

W₂=U₂-U₁=mC_V(T₂-T₁) Ponieważ T₂<T₁ praca będzie wydana kosztem energii wewnętrznej gazu.

3.Sprężanie izotermiczne:

Ponieważ V₃>V₄ praca będzie pobrana i zamieniona w całości na cieopło Q₂ w ilości równoważnej, oddane chłodnicy.

4.Sprężaie adiabatyczne:

W₄=mC_V(T₁-T₂)

Całkowita praca otrzymana w Cyklu Carnota:

Równanie Van der Waalsa:Gazy rzeczywiste nie stosują się dokładnie do praw Boyle'a i Gay-Lussaca. Van der Waals z założeń teorii kinetycznej gazów wyprowadził równanie, które znacznie lepiej oddaje zachowanie się gazów:

gdzie: a/V²-określa dodatkowe ciśnienie wynikające z istnienia sił przyciągających między molekułami gazu, tzw siły spójności Van der Waalsal; b-jest związane z objętością samych molekuł gazu, która to objętość jest stała i niezależna od ciśnienia. Wartość jej jest równa poczwórnej objętości molekuł. Odgrywa ona tym większą rolę im bardziej molekuły są zagęszczone; Dla gazów bardzo rozrzedzonych, gdy objętość V jest bardzo duża, oba wyrazy dodatkowe można pominąć i z tego równania otrzymujemy prostsze równanie Clapeyrona.

Przykład: -równanie izotermy gazu rzeczywistego:

dla przedziału p₁-p₂ mamy co najmniej 3 wartości objętości:

pkt A-dwie fazy:gazowa, ciekła. Zmniejszając objętość można skraplać

gaz:

pkt krytyczny-punkt w którym występują 3 stany skupienia. Powyżej występuje tylko i wyłącznie gaz. Im dalej od pkt krytycznego tym gaz jest bardziej doskonały:

Charakterystyczny jest pkt przegięcia: dp/dV=0; d²p/dV²=0

Krytyczne parametry z obliczenia pochodnych:T_k=8/27*a/Rb; p_k=1/27*a/b²; V_k=3b.Wprowadzamy parametry:θ=T/T_k; π=p/p_k; ϕ=V/V_k i podstawiamy do równania Van der Waalsa:

Najogólniejsza postać gazu.

Równanie Bernouliego:

Ciśnienie statyczne+ciśnienie wysokości+ ciśnienie prędkości jest wartością stałą wzdłuż linii prądu.

poziom odniesienia

W czasie dt przekroje przesuwają się kolejno o dS₁ i o dS₂. Struga znajduje się na wysokości BA-h₁; CD-h₂

Wnioski :

-Wentylator na statku:

Tworzy się podciśnienie które wyciąga powietrze z wewnątrz.

-w pkt. B prędkość cząsteczek cieczy będzie największa dlatego ciecz się obniży i statek się bardziej zanurzy:

-mijanie dwóch statków

Maxwella równania:podstawowe równania klasycznej teorii pola elektromagnetycznego. Wyrażają ścisły związek między polem elektrycznym i magnetycznym:

div B=0

div D=ρ (nad B, D, j znajduje się symbol wektora)

E-wektor natężenia pola elektrycznego; H-wektor natężenia pola magnetycznego;

B-wektor indukcji magnetycznej; D-wektor indukcji elektrycznej; ρ-gęstość ładunku elektrycznego; j-wektor gęstości prądu elektrycznego; a i b - stałe uzgadniające jednostki, zależne od wyboru układu jednostek (np. w MKS i SI a=1= b, w układzie Gaussa a=1/c, b=4, gdzie c - prędkość światła w próżni).

Wnioski:Podstawowym wnioskiem z powyższych równań jest istnienie fal elektromagnetycznych. Na równaniach Maxwella opiera się cała nauka o elektryczności oraz dziedziny techniki związane z wytwarzaniem, przekazywaniem i wykorzystaniem energii elektrycznej i fal elektromagnetycznych. Prawa Maxwella:II prawo-zmienne pole magnetyczne wytwarza wirowe i także zmienne pole elektryczne.

Przemiany gazu doskonałego. Równanie stanu gazu doskonałego. Równanie Clapeyrona. Przemiana izotermiczna: T=const. Prawo Boyle'a-Mariotte'a: w izotermicznej przemianie stałej masy gazu ciśnienie jest odwrotnie proporcjonalne do objętości p=p₁*V₁/V

pV=const.

Przemiana izohoryczna:V=const

Prawo Charlesa:w izohorycznej przemianie stałej masy gazu ciśnienie jest wprost proporcjonalne do temp w skali bezwzględnej.

p=p₁*T/T₁

p/T=cons

Przemiana izobaryczna:p=const

Prawo Gay-Lussaca:Objętość określonej masy gazu pod stałym ciśnieniem jest wprost proporcjonalna do jego temperatury bezwzględnej. V=V₁*T/T₁

Równanie stanu gazu doskonałego:

pV/T=const. Dla określonej masy m gazu stosunek iloczynu jego objętości V i ciśnienia p do temp bezwzględnej T jest stały i równy stosunkowi tych samych wielkości odniesionych do gazu w warunkach normalnych (V_o, p_o, T_o). Wartość tego stosunku odniesiona do jednego mola gazu jest dla wszystkich gazów jednakowa i nosi nazwę uniwersalnej stałej gazowej R.

V_op_o/T_o=R z tąd otrzymujemy Równanie Clapeyrona: pV=RT (dla 1 mola gazu)

Porównanie przemiany izohorycznej i izobarycznej:

-obie wymagają przepływu ciepła; -w obu występuje zmiana temperatury, co pociąga za sobą zmianę energii wewnętrznej; -w przemianie izohorycznej praca nie jest wykonywana; -w przemianie izobarycznej W=pΔV; - \Q_v\<\Q_p\; - Q_V=c_Vm(T₂-T₁) - Q_p=c_pm(T₂-T₁) -c_p,c_V-ciepła właściwe.

Comptona zjawisko:daje się tylk wytłumaczyć za pomocą korpuskularnej natury promieniowania. Jeżeli naświetlimy jakieś ciało promieniami Roentgena to ciało to staje się wtórnym źródłem rozproszonych promieni rentgenowskich. Przy naświetlaniu grafitu krótkofalowymi promieniami Compton stwierdził w promieniowaniu rozproszonym istnienie dłuższych fal, a więc o mniejszej częstotliwości. Przy dochodzeniu do zależności na długość fali i na prędkość elektronu odrzuconego postępujemy tak jak gdyby foton i elektron były kulkami doskonale sprężystymi i zachowują przy zderzeniu zasadę zachowania pędu i energii.

Δλ=λ_C(1-cosϕ) ; λ_C-długość Comptonowskiej fali dla elektronu.

Prędkość odrzuconego elektronu w przybliżeniu:

Związek między kątem odrzutu elektronu Ψ i kątem ϕ:

m_o-masa spoczynkowa elektronu.

Lorentza transformacja: Związek między współrzędnymi przestrzenno-czasowymi (x,y,z,t) i (x',y',z',t') dowolnego zjawiska fizycznego zachodzącego przy przejściu od inercjalnego układu odniesienia K(x,y,z,t) do poruszającego się względem niego wzdłuż osi x z prędkością V ruchem jednostajnym układu odniesienia K'(x',y',z',t'). Stosuje się przy V porównywalnych z prędkością światła.

Wszystkie wzory mechaniki relatywistycznej przechodzą we wzory mechaniki klasycznej gdy przyjmiemy c=∝

Skrócenie długości:obserwator w układzie ruchomym x',y',z' poruszającym się względem układu nieruchomego x,y,z, odmierza pewną długość L' na swojej osi x' L'(x₁',x₂'). Obserwator nieruchomy układu x,y,z wyznacza pkt o takich odciętych x₁,x₂ aby początek i koniec odcinka L' w tej samej chwili t mijały te pkt. Długość L' obserwator nieruchomy oceni jako:

tak samo oceni obserwator ruchomy odległość obserwatora nieruchomego

Podłużenie czasu. Czas własny.

Przedział czasu T' obserwatora ruchomego obserwator nieruchomy oceni jako dłuższy i odwrotnie:

Dodawanie prędkości:

V'-prędkość pkt względem ruchomego układu w kierunku osi x'

V-prędkość tego układu, względem układu, który przyjmujemy za nieruchomy

Dodawając prędkość za pomocą tego relatywistycznego wzoru nigdy nie otrzymamy prędkości większej od prędkości światła.

Ciało doskonale czarne to takie wyidealizowane ciało, które pochłania całkowicie nań promieniowanie tzn zdolność absorbcyjna tego ciała A(λ, T)=1 a jego zdolność emisyjna E(λ, T) w danej temperaturze jest maksymalna.

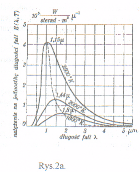
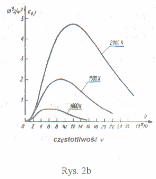
Rozkład natężenia promieniowania ciała doskonale czarnego w zależności od długości fali (2a), i od częstotliwości (2b). Na obu rysunkach widać przesunięcie maksimów w zależności od temperatury. Mechanizm ciała doskonale czarnego w oparciu o teorię Plancka: wg tej teorii (światło rozchodzi się jako zbiór fotonów) dało się wyjaśnić kształt krzywej z powyższych wykresów. Analityczna postać krzywych:

E(ν, T)=[(2πν²c ^-2 )]*[hν/(exp(hν/kT)-1)] gdzie: h-stała Plancka; T-temp w skali bezwzględnej;

Różniczkując ten wzór otrzymamy prawo Wiena: λ_max=b/T gdzie: b=2898*10 ^-6 [m*K]

natomiast prawo Stefana-Boltzmana otzymamy po obliczeniu pola pod krzywą daną wzorem Plancka:

E=σT⁴ gdzie:σ=5,67*10 ^-8 [W/m²K⁴]

Rozkład Boltzmana:

Jeśli mamy zbiór atomów w stanie równowagi termodynamicznej to liczba atomów w stanie wzbudzonym podlega prawu Boltzmana, które ma postać: N=N_oexp-(E-E_o)/kT;

gdzie: N_o-liczba atomów w stanie podstawowym; Nliczba atomów w stanie wzbudzonym; T-temp; k-stała Boltzmana

Rozkład Boltzmana oraz antyboltzmanowski rozkład atomów na poziomie podstawowym i pierwszym wzbudzonym.

---