Wydział Elektroniki Politechniki Wrocławskiej	Laboratorium fizyki ogólnej
^Wykonał Sławomir Wołek		^Grupa	^Ćw. nr 52	^Prowadzący mgr.Sitarek
Wyznaczanie ładunku właściwego elektronu		^Data wykonania 99.03.16	^Data oddania 99.03.23	^Ocena

CEL ĆWICZENIA:

Celem ćwiczenia jest umożliwienie praktycznego zapoznania się ze zjawiskami ruchu elektronów w polu elektrycznym i magnetycznym oraz z metodami wyznaczania ładunku właściwego elektronu. Porównanie dwóch metod pomiarowych ładunku właściwego.

WSTĘP:

Ładunek właściwy elektronu jest to stosunek jego ładunku e do jego masy, jest ważną stałą fizyczną występującą w równaniach balistyki i optyki elektronowej. Na podstawie doświadczalnie wyznaczonych wartości e oraz e/m obliczono masę elektronu.

Na elektron znajdujący się w polu elektrycznym o natężeniu
działa siła

Kierunek tej siły jest przeciwny do kierunku natężenia ze względu na ujemny ładunek elektronu.

Praca sił pola elektrycznego powoduje w przypadku elektronu swobodnego wyłącznie zmiany jego energii kinetycznej. Jeżeli elektron ze stanu spoczynku został rozpędzony do prędkości v przez pole elektryczne, przebywając przy tym różnicę potencjałów U, to zgodnie z zasadą zachowania energii

Można stąd obliczyć prędkość elektronu nabytą w polu elektrycznym

Na elektron poruszający się z prędkością
w polu magnetycznym o indukcji
działa siła

Zgodnie z własnościami iloczynu wektorowego siła
jest prostopadła do wektorów
i
, a jej wartość wynosi F=evBsinα. Pole magnetyczne nie działa na elektron znajdujący się w spoczynku lub poruszający się równolegle do wektora
. Ponieważ siła
jest stale prostopadła do kierunku ruchu elektronu, więc nie wykonuje ona żadnej pracy i nie zmienia energii kinetycznej elektronu. Siła F_m. osiąga wartość maksymalną, gdy elektron porusza się prostopadle do kierunku pola magnetycznego. Wtedy F_m.=evB.

W polu jednorodnym (
=constans ) siła F_m. ma charakter siły dośrodkowej, można zatem zapisać

W takim polu elektron porusza się po torze kołowym promieniu
. Okres obiegu elektronu wynosi
i jak widać nie zależy od wartości r i v. Ta właśnie własność jest wykorzystywana do pomiaru e/m metodą podłużnego pola magnetycznego.

1.Metoda poprzecznego pola magnetycznego ( metoda Thomsona ).

W metodzie tej odchylenie wiązki elektronów w poprzecznym polu magnetycznym kompensuje się za pomocą poprzecznego pola elektrycznego. Wiązka elektronów po odchyleniu w polu magnetycznym o kąt φ zostawia świecący ślad na ekranie luminescencyjnym S w odległości y od jego środka. Jednorodne pole magnetyczne o indukcji B, skierowane prostopadle do płaszczyzny rysunku, jest ograniczone do obszaru kołowego o średnicy l. Zakładając, że kąt φ jest mały, możemy napisać

gdzie L jest odległością ekranu od punktu wejścia elektronu w obszar pola. Po podstawieniu do tego wzoru wartości r otrzymamy :

Wychylenie y można skompensować, czyli sprowadzić wiązkę z powrotem do kierunku początkowego, za pomocą poprzecznego pola elektrycznego. Pole elektryczne wytwarza się przez przyłożenie napięcia do pary płytek odchylających, umieszczonych w obszarze działania pola magnetycznego. Aby kierunki odchylania wiązki elektronów przez oba pola pokrywały się, linie pola elektrycznego muszą być prostopadłe do linii pola magnetycznego. Jeżeli wychylenie y wiązki elektronów w polu magnetycznym zostanie skompensowane przez wychylenie (-y) tejże wiązki w polu elektrycznym, to w obszarze działanie obu pól musi być spełniony związek
Wynika stąd równość

EvB=eE

czyli

Podstawiając otrzymaną wartość v otrzymamy :

a stąd

przy czym l - średnica obszaru działania pola magnetycznego

L - odległość ekranu od punktu wejścia elektronów w pole magnetyczne.

W obliczeniach wykorzystałem wzór podany w opisie do ćwiczenia dostępnego w laboratorium

gdzie U - różnica potencjałów

y - odchylenie wiązki elektronów

B - indukcja magnetyczna

d - odległość płytek odchylających

D - średnica obszaru działania pola magnetycznego

L - odległość ekranu od punktu wejścia elektronów w polu magnetyczne

Indukcję B obliczamy ze wzoru :

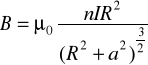
gdzie μ₀=4Π∙10^-7
- przenikalność magnetyczna próżni

n - ilość zwojów cewek

R - promień cewki

I - natężenie prądu

a - połowa odległości między cewkami

Schemat układu pomiarowego :

gdzie Z0-501,SN-103,SN-111 - zasilacze

C₁, C₂ - cewki

2.Metoda podłużnego pola magnetycznego.

Gdy elektron porusza się z prędkością v wzdłuż osi x równoległej do kierunku jednorodnego pola magnetycznego
, wówczas
i pole magnetyczne nie wpływa na jego ruch. Jeżeli jednak w pewnym punkcie A osi x elektron uzyska niewielką składową poprzeczną prędkości Δv, to tor jego ruchu z prostoliniowego zmieni się w spiralny. Ruch elektronu będzie wtedy superpozycją ruchu jednostajnego prostoliniowego z prędkością v wzdłuż osi x i ruchu jednostajnego po okręgu w płaszczyźnie prostopadłej do osi x z okresem obiegu T. Po wykonaniu pełnego obiegu, tzn. po czasie T, elektron przetnie oś x w punkcie A`. Odległość AA`=l wynosi :

Wartość składowej poprzecznej prędkości Δv nie ma wpływu na długość odcinka l. Inne elektrony podążające wzdłuż osi x z prędkością v, mimo że mogą uzyskać w punkcie A różne wartości Δv i poruszać się w związku z tym dalej po spiralach o różnych promieniach, przetną oś x również w punkcie A`. Nastąpi zatem zogniskowanie elektronów w punkcie A`. Położenie punktu A` na osi x zależy ponadto od wartości B. Można zatem przez zmianę wartości B spowodować zogniskowanie elektronów w zadanym punkcie (np. na ekranie luminescencyjnym ).

Prędkość poprzeczną Δv nadaje się elektronom przez zmiennego napięcia do pary płytek odchylających P₁P₂ położonych symetrycznie względem punktu A. Prędkość podłużną v uzyskują elektrony w polu wyrzutni elektronowej. Prędkość tę można wyrazić przez napięcie przyspieszające U. Przekształcenia wzorów zawartych w tej części sprawozdania dają ostateczny wzór :

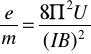
Indukcję B obliczamy ze wzoru :

gdzie N=
- ilość zwojów solenoidu podzielona przez długość solenoidu

Schemat układu pomiarowego :

gdzie S - solenoid

L - lampa oscyloskopowa

WYKAZ PRZYRZĄDÓW :

W metodzie Thomsona :

Urządzenie do pomiaru e/m typu LO-01

Zasilacz sieciowy typ ZJ-201

Zasilacz lampy sieciowej typ ZO-501

Stabilizator napięcia typ SN-111

Miliamperomierz LM-3 (klasa 0,5)

Woltomierz LM-3 (klasa 0,5)

W metodzie podłużnego pola :

Urządzenie do pomiaru e/m. typ LIF-04-025-1 (zawierające lampę oscyloskopową,

solenoid i woltomierz [kV] (klasa 1,5) )

Transformator zasilający urządzenie pomiarowe typ LIF-04-026-2

Miliamperomierz LM-3 (klasa 0,5)

Zasilacz prądu stałego do zasilania obwodu solenoidu typu SN-103 , 0-25 V

(stabilizator napięcia )

PRZEBIEG ĆWICZENIA :

1.Metodą Thomsona.

Po włączeniu zasilania lampy oscyloskopowej i wstępnym wyregulowaniu jasności, ostrości i położenia zerowego plamki świetlnej na ekranie, włączono prąd do obwodu cewek i regulując jego natężenie przesunięto plamkę o zadaną wartość y. Następnie przesunięcie to skompensowano przez doprowadzenie do płytek odchylających odpowiednio dobranej wartości napięcia U, przy którym plamka powróci w położenie zerowe. Pomiary wartości I oraz U wykonano dla kilku wybranych wartości y (5, 10, 15 i 20 mm) wychylając w górę i w dół.

Pomiary dla wychylenia w dół :

I (mA)	U (V)	y (mm)
9	10	5
21	23	10
32	35	15
42	47	21

Pomiary dla wychylenia w górę :

I (mA)	U (V)	y (mm)
11	13	5
23	25	10
34	39	15
45	51	20

Obliczenia :

n=650 - ilość zwojów

R=(50
1)mm=(0.05
0.001)m - promień cewki

d=(4,0
0,1)mm=(0.004
0.0001)m - odległość płytek odchylających

D=(100
1)mm=(0.1
0.001)m - średnica obszaru działania pola magnetycznego

L=(90
1)mm=(0.09
0.001)m. - odległość ekranu od punktu wejścia elektronu w pole magnetyczne

y=
0.5mm - dokładność odczytu położenia środka plamki

a=(38
1)mm=(0.038
0.001)m - połowa odległości między cewkami

U_z=75 V - zakres woltomierza

I_z=75 mA - zakres miliamperomierza

μ₀=
- przenikalność magnetyczna próżni

1.1.Obliczenia przy wychyleniu w dół :

y (mm)	B ( T )	e/m ( C/kg)
5	7,42	0,2533∙10^12
10	17,313	0,2127∙10^12
15	26,39	0,2705∙10^12
20	34,626	0,2178∙10^12

(e/m)_śr=23,86∙10¹⁰ C/kg

B_śr=21,437∙10^-5 T

Pomiar błędów :

gdzie t(p,n) - współczynnik studenta Fischera, t(p,n)=0,682

1.2.Obliczenia przy wychyleniu w górę

y (mm)	B ( T )	e/m ( C/kg )
5	9,068∙10^-5	0,219∙10^12
10	18,96∙10^-5	0,1925∙10^12
15	28,03∙10^-5	0,2068∙10^12
20	37,102∙10^-5	0,2057∙10^1^2

(e/m)_śr=20,6∙10¹⁰ C/kg

B_śr=23,29∙10^-5 T

Pomiar błędów :

2.Metodą podłużnego pola magnetycznego.

Po włączeniu prądu w obwodzie solenoidu i w miarę zwiększania jego natężenia świecący odcinek na ekranie ulega coraz większemu skręceniu i skróceniu. Przyczyną tego zjawiska jest zmiana torów elektronów z prostoliniowych na tory spiralne. Regulując natężenie prądu płynącego przez solenoid można uzyskać zredukowanie śladu wiązki elektronów na ekranie do punktu.

Pomiary przy wychyleniu poziomym :

L_x=22,1cm=0,221 m

U [ kV ]	I [ mA ]
0,65	640-300=340
0,75	660-310=350
0,9	680-320=360
1	690-325=365
1,1	710-330=380
1,2	720-330=390
1,3	730-330=400
1,4	740-335=405
1,5	750-340=410

Objaśnienie do tabelki :

Dla napięcia U równego np. 650 V zaobserwowano cienką jasną plamkę przy natężeniu I=0,300 A oraz plamkę cieńszą przy natężeniu 0,640 A. Różnica tych natężeń posłuży do obliczeń.

Pomiary przy wychyleniu pionowym :

L_y=18,3cm=0,183 m

U [kV ]	I [ mA ]
0,7	420
0,8	440
0,9	460
1	470
1,1	490
1,2	500
1,3	520
1,4	530
1,5	530

Objaśnienie do tabelki :

Dla napięcia U równego np. 700 V zaobserwowano cienką jasną plamkę przy natężeniu I=0,420 A oraz cieńszą plamkę, dla której wartość natężenia wykraczała poza zakres miernika.

Obliczenia :

N=
=(7200
50) - ilość zwojów solenoidu podzielona przez długość solenoidu

L_x=22.1 cm=0,221 m

L_y=18.3 cm=0,183 m.

U_z=1500 V - zakres woltomierza

I_z=0,750 A - zakres miliamperomierza

2.1.Obliczenia przy wychyleniu poziomym :

U [kV ]	B [ T ]	e/m [ C/kg]
0,65	3,076	11,1056
0,75	3,166	12,0960
0,9	3,257	13,7155
1	3,302	14,8269
1,1	3,438	15,0448
1,2	3,528	15,5858
1,3	3,620	16,0373
1,4	3,664	16,8586
1,5	3,710	17,6176

(e/m)_śr=15,0986∙10¹⁰ C/kg

B_śr=3,418∙10^-3 T

Pomiar błędów :

Ponieważ pomiarów było więcej niż 6 błąd ΔB liczymy ze wzoru :

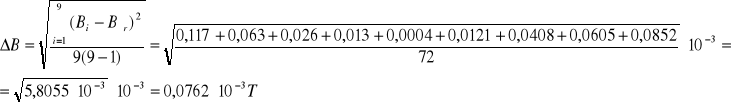
2.2.Obliczenia przy wychyleniu pionowym :

U [ kV ]	B [ T ]	e/m ( C/kg )
0,7	3,8	11,43
0,8	3,98	11,907
0,9	4,162	12,25
1	4,252	13,04
1,1	4,433	13,197
1,2	4,524	13,82
1,3	4,705	13,845
1,4	4,8	14,326
1,5	4,8	15,35

B_śr=4,384∙10^-3 T

(e/m)_śr=13,2405∙10¹⁰ C/kg

Pomiar błędów :

WNIOSKI I UWAGI:

•Metoda poprzecznego pola ma dziś znaczenie bardziej historyczne, ze względu na zbyt duże uproszczenia przyjętych założeń.

•W większości obliczeń wystąpił błąd systematyczny wynikający z przybliżonych wartości większości stałych.

•Wystąpił także inny błąd systematyczny (błąd pomiarów) spowodowany niemożliwością dokładnego odczytu wartości wskazywanych przez przyrządy (oscyloskopy - średnica plamki) oraz zbyt małym zakresem przyrządów (np. w przypadku natężenia w metodzie podłużnego pola ).

•Metoda Thomsona jest również mniej dokładna od metody podłużnego pola. O ile w przypadku pierwszej metody błędy wynosiły .28,56% i 35,73%, o tyle w przypadku drugiej metody błędy były kilkakrotnie mniejsze i wynosiły 7,14% i 7,56%.

•Fakt, że wartość e/m podana w tablicach ( 17,588∙10¹⁰ C/kg ) nie mieści się w przedziałach wartości obliczonych za pomocą metody podłużnego pola ( przy małych błędach względnych ) wynika m.in. ze zbyt małego zakresu wartości mierzonych przez miernik napięcia a zwłaszcza przez miernik natężenia oraz niedokładności odczytu ).

---