Wydział Budownictwa i Inżynierii Środowiska

Uniwersytet Technologiczno-Przyrodniczy

im. Jana i Jędrzeja Śniadeckich

w Bydgoszczy

Konstrukcje Metalowe

Ćwiczenie projektowe nr 3

SILOS STALOWY

Wykonała studentka: Żaneta Wiśniewska gr. C_KBI

Prowadzący: mgr inż. Jan Górski

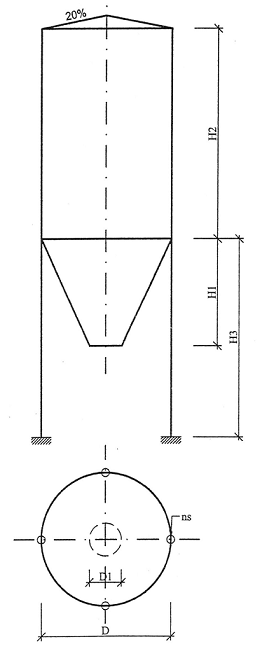
1. Założenia do projektu

1.1.Dane projektowe.

• Stal: St3S,

• Materiał wypełniający: pył węglowy →μ = 0,50,

• Liczba slupów: 4 ,

• Strefa klimatyczna: II,

1.2 Geometria silosu.

Wymiary: D = 4,34,

H₁ = 2,64,

H₂ = 8,97,

H₃ = 5,73,

H₄ = 0,42-wysokość przekrycia

D₁ = 0,78,

α = 56° - kąt pochylenia ściany leja,

2. Obliczenia statyczne i wymiarowanie (wg PN-B-03202:1996).

2.1. Obliczenie naporu materiału sypkiego na ściany silosu.

2.1.1 Określenie rodzaju przepływu.

Zgodnie z rysunkiem 3 PN-B-03202:1996 dla μ = 0,50, oraz α = 56° ustalono że w silosie wystąpi przepływ rdzeniowy.

2.1.2 Napór po napełnieniu komory.

gdzie:

p_wf, p_hf, p_vf - wartości naporu po napełnieniu, odpowiednio stycznego, poziomego i pionowego, [kPa],

P_wf - suma oddziaływań stycznych na jednostkę obwodu komory,

z - odległość rozpatrywanego przekroju od maksymalnego wyrównanego materiału sypkiego,

γ - ciężar objętościowy materiału sypkiego,

A - pole powierzchni wewnętrznej przekroju poziomego komory silosu,

u - obwód wewnętrzny komory,

μ - współczynnik tarcia o pobocznice silosu składowanego materiału,

λ - stosunek naporu poziomego do pionowego,

φ (z) - funkcja określona wzorem: φ (z) = 1-e^(-z/zo).

γ = 8,00kN/m³,

A =π·r² = 3,14·2,17² = 14,79m²,

u =2·π·r = 2·3,14·2,17 = 13,63m,

μ=0,50,

λ = 0,70,

2.1.3 Napór po opróżnianiu komory.

a) Równomierny.

p_we = e_w ·p_wf,

p_he = e_h ·p_hf,

gdzie:

p_we, p_he - wartości naporu przy opróżnianiu, [kPa],

e_w, e_h -współczynniki zwiększające, określone w zależności od h/d,

h = H₁ + H₂ +1/3H₄ = 2,64+8,97 + 1/3·0,42 = 11,75m

→ e_w = 1,1,

e_h = e_h0 = 1,20.

b) Nierównomierny.

Komora silosu jest przekroju kołowego, oraz posiada usztywnienia poziome na końcach. Zastosowano zatem do obliczeń uproszczony sposób, przyjmując zastępcze oddziaływanie równomierne p_he2.

p_he2 = χ·p_he

gdzie:

χ - współczynnik zwiększający, określony w zależności o r/t,

r = 2,17m,

t = 0,008m,

→

β - parametr nierównomierności naporu,

β = β_h · β_a · β_r · β_G

dla 1,0 ≤
=2,71 ≤ 4,0,

β_a = 1,0 dla
<
,

a - mimośród osi otworu wylotowego, a = 0,

β_r = 0,05 dla

β_G =0,50,

β = 1,34· 1,0 · 0,05 · 0,50 = 0,03354

2.1.4 Napór na lej wysypowy.

a) Napór od materiału sypkiego zawartego w leju.

l = 3,18m,

l/4 = 3,18/4 = 0,795m.

b) Napór od materiału powyżej leja.

p_{n1 ­} - wartość składowej normalnej naporu przy górnym brzegu leja, kPa

c_b =1,8,

p_vf = 23,487kPa dla z = 9,11m,

p_hf = 16,441kPa dla z = 9,11m,

α = 56°,

p_n2 - wartość składowej normalnej naporu przy dolnym brzegu leja, kPa

1. Oddziaływania uwzględniane przy sprawdzaniu stateczności ścian komory.

1. Zastępcze oddziaływania powiększone:

p_ws = 1,1p_we,

2. Napór poziomy ustateczniający ścianę:

należy przyjmować dla przepływu rdzeniowego ≥
, a = 0, d = 4,34m.

Zatem przyjęto
= 0,16667.

p_hs = 0,3333·p_hf.

2.1. 6 Zestawienie wartości naporów

Napór od materiału sypkiego zawartego w leju:
pn pw	14,17kPa 7,084kPa

Napór od materiału powyżej leja:
pn1 pn2 pw1 pw2	35,89kPa 13,22kPa 17,95kPa 6,61kPa

Rzędna	Napór po napełnianiu komory						Napór po opróżnianiu					Oddziaływania przy sprawdzaniu stateczności ścian komory
														Napór równomierny			Napór nierównomierny
z	pwf	pwf średnie	phf	phf średnie	pvf	Pwf	pwe	pwe średnie	phe	phe2	phe2 średnie	pws	phs
m	kPa				kPa		kPa		kPa	kPa			kPa	kPa		kPa	kPa
0,0	0,0		0,0		0,0	0,0	0,0		0,0	0,0		0,0	0,0
0,11	0,3026		0,6052		0,8646	0,0167	0,3329		0,7262	0,8465		0,3661	0,1816
0,61	1,5505	2,0814	3,1009	4,1629	4,4299	0,4884	1,7055	2,2896	3,7211	4,3371	5,8224	1,8761	0,9303
1,11	2,6124		5,2249		7,4641	1,5362	2,8737		6,2698	7,3078		3,1610	1,5675
1,61	3,5162	3,9008	7,0325	7,8016	10,0464	3,0745	3,8679	4,2909	8,4390	9,8360	10,9118	4,2546	2,1097
2,11	4,2854		8,5708		12,2440	5,0301	4,7139		10,2850	11,9876		5,1853	2,5712
2,61	4,9400	5,2185	9,8800	10,4371	14,1143	7,3408	5,4340	5,7404	11,8560	13,8187	14,5979	5,9774	2,9640
3,11	5,4971		10,9942		15,7060	9,9538	6,0468		13,1930	15,3771		6,6515	3,2983
3,61	5,9712	6,1729	11,9424	12,3459	17,0606	12,8241	6,5683	6,7902	14,3309	16,7033	17,2676	7,2252	3,5827
4,11	6,3747		12,7494		18,2134	15,9133	7,0122		15,2993	17,8320		7,7134	3,8248
4,61	6,7181	6,8642	13,4362	13,7284	19,1945	19,1888	7,3899	7,5506	16,1234	18,7925	19,2013	8,1289	4,0308
5,11	7,0103		14,0206		20,0295	22,6228	7,7113		16,8248	19,6100		8,4825	4,2062
5,61	7,2590	7,3649	14,5180	14,7297	20,7401	26,1918	7,9849	8,1013	17,4217	20,3057	20,6018	8,7834	4,3554
6,11	7,4707		14,9414		21,3448	29,8757	8,2178		17,9296	20,8978		9,0395	4,4824
6,61	7,6508	7,7275	15,3016	15,4549	21,8595	33,6573	8,4159	8,5002	18,3620	21,4017	21,6161	9,2575	4,5905
7,11	7,8041		15,6082		22,2975	37,5220	8,5845		18,7299	21,8305		9,4430	4,6825
7,61	7,9346	7,9901	15,8692	15,9802	22,7	41,4576	8,7280	8,7891	19,0430	22,1955	22,3508	9,6009	4,7608
8,11	8,0456		16,0912		22,9875	45,4534	8,8502		19,3095	22,5061		9,7352	4,8274
8,61	8,1401	8,1803	16,2802	16,3606	23,2575	49,5004	8,9541	8,9984	19,5363	22,7704	22,8829	9,8495	4,8841
9,11	8,2205		16,4411		23,4872	53,5911	9,0426		19,7293	22,9954		9,9468	4,9323

5. Obciążenie wiatrem (wg PN-77/B-02011)

p_k = q_k · C_e ·C·β

p = p_k ·γ_f

γ_f=1,3 wg pkt. 2.3 PN-77/B-02011

q_k=0,35 kPa - II strefa wiatrowa,

β=1,8

z=15,134m

C_e=0,8+0,02·z = 0,8+0,02·15,134 = 1,103

Współczynnik aerodynamiczny C_z wg Z1-12 PN-77/B-02011.

D = 4,34m,

H = 15,134m,

D/H = 0,287,

k = 1,048493

a₀ = -0,356, a₂ = 0,636, a₄ = 0,058, a₆ =- 0,034.

a₁ = 0,322, a₃ = 0,501, a₅ = -0,128,

C_z =C_α dla C_α >0,

C_z =C_α ·k dla C_α<0

Tabela - zestawienie obciążeń od wiatru.

kąt		Cα	Cz	pk
0	0,00	0,9990	0,9990	0,6940
6	0,1047	0,9774	0,9774	0,6790
12	0,2094	0,9096	0,9096	0,6319
18	0,3142	0,7877	0,7877	0,5472
24	0,4189	0,6040	0,6040	0,4196
30	0,5236	0,3567	0,3567	0,2478
36	0,6283	0,0548	0,0548	0,0381
42	0,7330	-0,2801	-0,2937	-0,2040
48	0,8378	-0,6156	-0,6454	-0,4484
54	0,9425	-0,9142	-0,9585	-0,6659
60	1,0472	-1,1410	-1,1963	-0,8311
66	1,1519	-1,2715	-1,3332	-0,9261
72	1,2566	-1,2969	-1,3598	-0,9447
78	1,3614	-1,2261	-1,2855	-0,8930
84	1,4661	-1,0828	-1,1353	-0,7887
90	1,5708	-0,9000	-0,9436	-0,6555
96	1,6755	-0,7125	-0,7470	-0,5189
102	1,7802	-0,5493	-0,5760	-0,4001
108	1,8850	-0,4293	-0,4501	-0,3127
114	1,9897	-0,4	-0,4194	-0,2914
120	2,0944	-0,4	-0,4194	-0,2914
126	2,1991	-0,4	-0,4194	-0,2914
132	2,3038	-0,4	-0,4194	-0,2914
138	2,4086	-0,4	-0,4194	-0,2914
144	2,5133	-0,4	-0,4194	-0,2914
150	2,6180	-0,4	-0,4194	-0,2914
156	2,7227	-0,4	-0,4194	-0,2914
162	2,8274	-0,4	-0,4194	-0,2914
168	2,9322	-0,4	-0,4194	-0,2914
174	3,0369	-0,4	-0,4194	-0,2914
180	3,1416	-0,4	-0,4194	-0,2914

2.2. Zestawienie obciążeń i kombinacji.

2.2.1. Obciążenia:

1. Ciężar własny

2. pwf

3. phf

4. pwe

5. phe2

6. Napór od materiału w leju

7. Napór od materiału powyżej leja

8. Wiatr1

17. Śnieg

18. Wiatr2

2.2.2. Kombinacje obciążeń:

Kombinacja	Nazwa	Typ analizy	Natura kombinacji	Natura przypadku	Definicja
23 (K)	KOMB1	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(2+3+6+7)*1.20+8*1.30+17*1.50
24 (K)	KOMB2	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(2+3+6+7)*1.20+18*1.30+17*1.50
25 (K)	KOMB3	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(2+3+6+7)*1.20+17*1.50
26 (K)	KOMB4	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(4+6+7)*1.20+3*1.44+8*1.30+17*1.50
27 (K)	KOMB5	Kombinacja liniowa	SGN	ciężar własny	1*1.10+3*1.44+(4+6+7)*1.20+17*1.50+18*1.30
28 (K)	KOMB6	Kombinacja liniowa	SGN	ciężar własny	1*1.10+3*1.44+(4+6+7)*1.20+17*1.50
29 (K)	KOMB7	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(4+5+6+7)*1.20+8*1.30+17*1.50
30 (K)	KOMB8	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(4+5+6+7)*1.20+17*1.50+18*1.30
31 (K)	KOMB9	Kombinacja liniowa	SGN	ciężar własny	1*1.10+(4+5+6+7)*1.20+17*1.50
32 (K)	KOMB10	Kombinacja liniowa	SGN	ciężar własny	1*1.10+4*1.32+3*0.40+(6+7)*1.20+8*1.30+17*1.50
33 (K)	KOMB11	Kombinacja liniowa	SGN	ciężar własny	1*1.10+3*0.40+4*1.32+(6+7)*1.20+17*1.50+18*1.30
34 (K)	KOMB12	Kombinacja liniowa	SGN	ciężar własny	1*1.10+3*0.40+4*1.32+(6+7)*1.20+17*1.50
35 (K)	KOMB13	Kombinacja liniowa	SGN	ciężar własny	1*1.10+18*1.30

3. Sprawdzenie nośności walcowego płaszcza z uwzględnieniem stateczności.

3.1 Wymiarowanie powłoki walcowej.

3.1.1 Geometria płaszcza.

Dla ściskania podłużnego:

Dla ściskania obwodowego:

gdzie:

r- promień krzywizny ściany komory;

t- grubość ściany komory;

l- długość powłoki płaszcza;

C_φ- współczynnik zależny od sposobu podparcia obu brzegów powłoki

3.1.2 Współczynnik niestateczności miejscowej k_x.

Smukłość względna powłoki:

(A-4)

Naprężenia krytyczne dla wzdłuż osi tworzącej:

(A-5)

(A-6)

Współczynniki odchyłek geometrycznych.

Przyjęto 2 klasę dokładności wykonania →(δ_o < δ < 2δ_o )

(A-10)

(A-12)

Współczynnik niestateczności miejscowej: k_x=k_b·k₂

3.1.3 Współczynnik niestateczności miejscowej k_φ.

Smukłość względna powłoki;

(A-4)

Naprężenia krytyczne dla ściskania obwodowego:

(A-7)

C_φ =1,0 dla warunków podparcia WP2, WP2

Współczynniki odchyłek geometrycznych.

Przyjęto 2 klasę dokładności wykonania (δ₀ <δ < 2δ₀ )

(A-10)

(A-11)

Współczynnik niestateczności miejscowej: kφ= k_b · k₂

3.2 Częściowy współczynnik bezpieczeństwa γ_d przy utracie stateczności.

Dla powłok klasy 2 dokładności wykonania;

(A-15)

3.3 Wytrzymałość obliczeniowa na wyboczenie.

Naprężeń ściskające w kierunku podłużnym:

(A-19)

Naprężeń ściskające w kierunku obwodowym:

(A-20)

3.4 Warunek stateczności miejscowej przy dwukierunkowym stanie naprężeń.

(A-18)

4. Obliczenie nośności płaszcza walcowego.

SPRAWDZENIE NOŚNOŚCI WALCOWEGO PŁASZCZA
Z UWZGLĘDNIENIEM STATECZNOŚCI
Geometria płaszcza dla t = 10mm
r/t =	217,00	≤	2500
a)ściskanie podłużne
l/r =	4,13	≤	7,37
b)ściskanie obwodowe		Cφ =	1,00
l/r =	4,13	≤	24,01
Współczynnik niestateczności miejscowej kx i kφ
a)smukłość względna powłoki
λsx =	0,66	<	1,5
σcrx =	571,77	MPa
Cx =	1,00
λsφ =	4,16	≥	1,5
σcrφ =	14,27	MPa
b)współczynnik odchyłek geometrycznych k2 powłoki
λsx <1,5 	k2x =	0,89
λsφ ≥1,5 	k2φ =	0,75
δδ 	1,50
c)współczynniki wyboczeniowe ka, kb
λsφ ≥ 1,2		ka =	0,04
0,25< λsx ≤1,0		kb =	0,62
d)współczynnik niestateczności miejscowej k
k2x :	kx =	0,55
k2φ :	kφ =	0,03
Częściowy współczynnik bezpieczeństwa γd przy utracie stateczności
0,25< λsx <2,0 :	γd =	1,18		λsφ ≥ 2,0 :	γd =	1,45
Warunek stateczności miejscowej przy dwukierunkowym stanie naprężeń
	σRX =	115,43	MPa
	σRφ =	4,80	MPa

Geometria płaszcza dla t = 8mm
r/t =	271,25	≤	2500
a)ściskanie podłużne
l/r =	4,13	≤	8,23
b)ściskanie obwodowe		Cφ =	1,00
l/r =	4,13	≤	26,85
Współczynnik niestateczności miejscowej kx i kφ
a)smukłość względna powłoki
λsx =	0,74	<	1,5
σcrx =	457,38	MPa
Cx =	1,00
λsφ =	4,92	≥	1,5
σcrφ =	10,21	MPa
b)współczynnik odchyłek geometrycznych k2 powłoki
λsx <1,5 	k2x =	0,88
λsφ ≥1,5 	k2φ =	0,75
δδ 	1,50
c)współczynniki wyboczeniowe ka, kb
λsφ ≥ 1,2		ka =	0,03
0,25< λsx ≤1,0		kb =	0,55
d)współczynnik niestateczności miejscowej k
k2x :	kx =	0,48
k2φ :	kφ =	0,02
Częściowy współczynnik bezpieczeństwa γd przy utracie stateczności
0,25< λsx <2,0 :	γd =	1,20		λsφ ≥ 2,0 :	γd =	1,45
Warunek stateczności miejscowej przy dwukierunkowym stanie naprężeń
	σRX =	99,15	MPa
	σRφ =	3,43	MPa

Geometria płaszcza dla t = 6mm
r/t =	361,67	≤	2500
a)ściskanie podłużne
l/r =	4,13	≤	9,51
b)ściskanie obwodowe		Cφ =	1,00
l/r =	4,13	≤	31,00
Współczynnik niestateczności miejscowej kx i kφ
a)smukłość względna powłoki
λsx =	0,85	<	1,5
σcrx =	343,01	MPa
Cx =	1,00
λsφ =	6,11	≥	1,5
σcrφ =	6,63	MPa
b)współczynnik odchyłek geometrycznych k2 powłoki
λsx <1,5 	k2x =	0,86
λsφ ≥1,5 	k2φ =	0,75
δδ 	1,50
c)współczynniki wyboczeniowe ka, kb
λsφ ≥ 1,2		ka =	0,02
0,25< λsx ≤1,0		kb =	0,44
d)współczynnik niestateczności miejscowej k
k2x :	kx =	0,38
k2φ :	kφ =	0,01
Częściowy współczynnik bezpieczeństwa γd przy utracie stateczności
0,25< λsx <2,0 :	γd =	1,22		λsφ ≥ 2,0 :	γd =	1,45
Warunek stateczności miejscowej przy dwukierunkowym stanie naprężeń
	σRX =	76,72	MPa
	σRφ =	2,23	MPa

5. Porównanie wyników obliczeń z programu Robot z wartościami dopuszczalnymi ustalonymi na podstawie PN-88/B-03004 i PN-90/B-03200

Uwaga: Obliczenia w programie Robot wykonano dla grubości ścian już po uwzględnieniu warstwy ścieralnej.

• naprężenia w powłoce silosu

warunek stateczności i wytrzymałości: σ_xx < σ_kr, σ_yy < σ_krφ, σ_max< f_d

Wartości dopuszczalne dla t = 8mm

f_d = 215MPa

σ_kr = -99,15MPa

σ_krφ = -3,43MPa

panel 1 (t=8mm) - lej wysypowy

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	15,58	12,64	2,05
Element	675	678	4
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-2,05	0,49	-2,21
Element	128	1	12
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

panel 2 (t=8mm) - lej wysypowy

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	24,70	16,33	4,07
Element	1095	1008	1127
Przypadek	32 (K)	32 (K)	32 (K)
MIN	6,75	-0,4	-3,99
Element	785	1136	1109
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

panel 3 (t=8mm) - 1 panel od dołu

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	16,01	5,21	13,11
Element	2094	1395	1322
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-77,19	-0,24	-13,35
Element	1366	1323	1334
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

Wartości dopuszczalne dla t = 6mm

f_d = 215MPa

σ_kr = -76,72MPa

σ_krφ = -2,23MPa

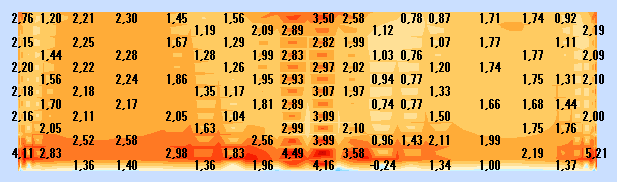
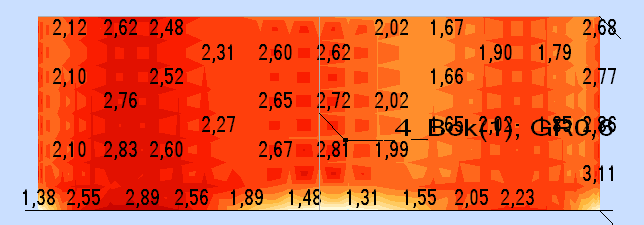
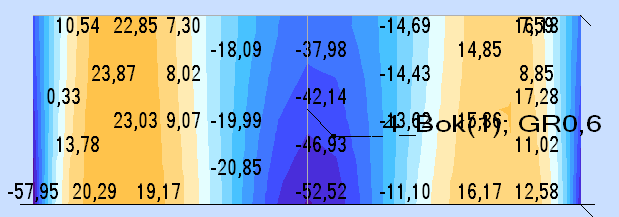
panel 4 (t= 6mm) - 2 panel od dołu

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	23,87	3,11	5,9
Element	2513	2236	2163
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-57,95	1,31	-6,1
Element	2206	2162	2173
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

panel 5 (t=6mm) - 3 panel od dołu

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	23,36	2,7	3,7
Element	2693	2656	2644
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-38,71	1,57	-3,84
Element	2686	3007	2652
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

panel 6 (t=6mm) - 4 panel od dołu

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	18,61	2,35	3,19
Element	3173	3137	3169
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-26,48	1,21	-3,19
Element	3166	3488	3147
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

panel 7 (t=6mm) - 5 panel od dołu

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	12,75	1,96	3,18
Element	3654	3618	4010
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-16,73	0,74	-3,09
Element	3646	3968	3626
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

panel 8 (t=6mm) - 6 panel od dołu

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	6,56	1,38	3,33
Element	4134	4099	4490
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-7,87	-0,45	-3,12
Element	4126	4447	4466
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx

Rozkład naprężeń Syy

Wartości dopuszczalne dla t = 8mm

f_d = 215MPa

σ_kr = -99,15MPa

σ_krφ = -3,43MPa

panel 9 (t=8mm) - stożek dachowy

	sXX (MPa)	sYY (MPa)	sXY (MPa)
MAX	0,73	5,92	0,99
Element	4911	4591	4610
Przypadek	32 (K)	32 (K)	32 (K)
MIN	-1,8	-2,29	-0,93
Element	4628	4658	4586
Przypadek	32 (K)	32 (K)	32 (K)

Rozkład naprężeń Sxx Rozkład naprężeń Syy

6. Sprawdzenie nośności pierścienia podporowego

W celu przeniesienia siły z pierścienia na słup poprzez docisk, przyjęto blachę łącząca pierścień z głowicą słupa grubości 14mm.

Schemat do wyznaczenia momentu bezwładności przekroju pierścienia wraz z przekrojem współpracującym płaszcza i leja

Nośność pierścienia podporowego obciążonego promieniowymi oddziaływaniami leja z uwzględnieniem obciążającego wpływu naporu materiału składowanego, sprawdzono według wzoru:

n- połowa liczby słupów;

I_y- moment bezwładności przekroju pierścienia (wraz z przekrojem współpracującym płaszcza i leja) względem osi pionowej y, w milimetrach do czwartej;

R- promień pierścienia (odniesiony do środka ciężkości przekroju, w milimetrach)

n=2

E=205000 MPa

Iy=7712884 mm⁴

R=2170 mm

Podstawiając otrzymujemy:

γ_d =1,5

Wartość q otrzymana na podstawie obliczeń uzyskanych w programie Robot

q=(1294,995/13,63) ·cos56 = 53,13 kN/m

q = 53,13 kN/m < q_kr=309,47kN/m- warunek został spełniony.

7. Sprawdzenie warunku ekstremalnych naprężeń.

Naprężenia maksymalne Smax < f_d = 215MPa

Naprężenia w płaszczu

	NXX (kN/m)	s1 (MPa)	s2 (MPa)	sMises (MPa)	sXX (MPa)	sYY (MPa)
MAX	211,1696	26,43	15,62	79,93	26,4	16,39 < fd
Element	1155	1155	990	1275	1155	973
Przypadek	32 (K)	32 (K)	33 (K)	33 (K)	32 (K)	33 (K)
MIN	-716,472	-34,7	-89,56	0,26	-89,56	-34,7
Element	1215	1215	1215	4868	1215	1215
Przypadek	33 (K)	33 (K)	33 (K)	34 (K)	33 (K)	33 (K)

Naprężenia Sxx Naprężenia S_YY

Naprężenia w pierścieniu

	S max(My) (MPa)	S max(Mz) (MPa)	S min(My) (MPa)	S min(Mz) (MPa)
MAX	154,22	84,36	-1,17	-0,02 < fd
Pręt	58	11	15	13
Węzeł	1298	1283	1338	1341
Przypadek	33 (K)	32 (K)	30 (K)	23 (K)
MIN	1,17	0,01	-154,22	-30,66
Pręt	15	13	58	61
Węzeł	1338	1341	1298	1294
Przypadek	30 (K)	23 (K)	33 (K)	30 (K)

8. Nośność słupa

Na słupy przyjęto przekrój rurowy RO 355.6x10

Na podstawie programu Robot określono, że najbardziej niekorzystne kombinacje sił działających na słup są kombinacja 11.

N = 607,405kN

M_x =18,34kNm

M_y = 6,39kNm

N_RC = ψAf_d

ψ = 1,0 → I klasa

A = 0,0109m²

fd = 215MPa → Stal ST3S

N_RC = 1,0·0,0109·215000=2343,5kN

Przyjęto wartość współczynnika wyboczeniowego μ_y = 2

I_y = 16220,0cm⁴

N_cr = 2498,82 kN

→ l₁ = 5,73m ≤ 100b₀
= 100·0,39·
=39m

β_x= β_y = 1,0

M_RX = M_RY = ψ·W_c· f_d = 1,0·1824,916·10^-6·215000=392,36kNm

0,381+0,047+0,016 =0,469

Nośność słupa jest zapewniona

9. Zaprojektowanie połączenia słupa z fundamentem na podst. PN-B-03215:1998

W obliczeniach wzięto pod uwagę kombinacje 11 obciążeń (pełny silos +wiatr) - kombinacja ta wykazuje największe wartości siły normalnej, w porównaniu do momentów Mx i My, oraz kombinacje 13 (pusty silos +wiatr).

1. Wpływ sił działających na słup w kombinacji 11.

Ze względu na niewielkie momenty Mx i My w porównaniu do siły normalnej połączenie słupa z fundamentem zaprojektowano jako osiowo ściskane.

N_C ≤N_RC =A_c·f_b

f_b = 10,6MPa→dla B20

Ac = π·R² = π·0,318² = 0,32m²

N_c = 607,405 < N_Rc = 0,32·10600 = 3392kN.

Wyznaczenie grubości blachy podstawy

→ ω =0,124

f_d = 215MPa

Podstawa słupa zostanie zamocowana do fundamentu za pomocą 8 śrub F20

Wyznaczenie grubości spoiny łączącej słup z płytką podstawy słupa.

Zastosowano spoinę pachwinową o grubości a=8mm

0,2t₁ < a < 0,7t₂ 0,2x10=2mm < a < 0,7x15=10,5mm

κ=0,7

l= 2πr = 2·π·0,178=1,12m

Rzeczywiste naprężenia w spoinie będą mniejsze ponieważ część naprężeń przejmą żebra usztywniające płytkę podstawy.

Przyjęto konstrukcyjnie żebra podstawy słupa grubości 12mm i spoinę 5mm.

2. Wpływ sił działających na słup przy kombinacji 13.

Kombinację tą wzięto pod uwagę ze względu na znaczny moment zginający My=14,26 kNm i niewielką siłę normalną równą N=50,53 kN.

Określenie kąta strefy docisku

r =0,124m

b_c = 0,17m

E = 205GPa

E_c = 29GPa

α=52°

Naprężenia docisku:

σ_c =0,142 MPa < f_b = 10,6MPa

Naprężenia w stali:

10. Zaprojektowanie głowicy słupa

Siła ściskająca działająca na głowicę:

N=592,95kN,

T=1,25kN

Przyjęto konstrukcyjnie blachę czołową gr. 12mm

Sprawdzenie nośności spoiny pachwinowej łączącej słup z blachą poziomą.

Zastosowano spoinę pachwinową o grubości a=6mm

0,2t₁ < a < 0,7t₂ 0,2x12=2,4mm < a < 0,7x12=8,4mm

κ=0,7

l= 2πr = 2·π·0,178=1,12m

Obliczenie długości spoiny pachwinowej a=6mm potrzebnej do przeniesienia reakcji N=592,95kN.

Długość pionowych spawów użebrowania musi być większa niż 0,57m.

Sprawdzenie nośności śrub na ścianie.

Przyjęto konstrukcyjnie 4śruby M16 (4,8) mocujące słup z pierścieniem podporowym.

S_Rv=38,0kN,

F=1,25kN < n ·S_RV=4·38,0=152kN → Nośność śrub na ścinanie jest zapewniona.

Sprawdzenie nośności przepony:

h = 180mm

l= 370mm

d= 12mm

N= 592,95kN

Przyjęto schemat belki wolnopodpartej i obciążenie rozłożone:

Nośność przepony jest wystarczająca.

32

---