Rok akademicki 2009/2010

Sprawozdanie

do ćw. nr 13

Temat:

Badanie centralnych zderzeń sprężystych i niesprężystych

Wykonał:

Piotr Maślanka Lp 5

I Część teoretyczna.

Zasada zachowania energii - w układzie izolowanym suma składników wszystkich rodzajów energii całości (suma energii wszystkich jego części) układu jest stała (nie zmienia się w czasie).

Zasada zachowania energii w mechanice klasycznej i kwantowej jest konsekwencją symetrii translacji (przesunięć) w czasie. Ma ona jednak w fizyce szersze znaczenie. Przyjmuje się, że zasada zachowania energii jest spełniona również w układach nieprzejawiających takiej symetrii i nie dających się opisywać przy użyciu formalizmu hamiltonowskiego. W ramach tego formalizmu wyprowadzany jest związek między zasadami zachowania a symetriami układów fizycznych. Przykładami takich układów są:

• układy opisywane przez fizykę statystyczną, gdzie symetria w czasie dla całego układu nie jest zachowana,

• układy związane z występowaniem siły tarcia,

• inne układy na przykład cechujące się przemianami nierównowagowymi, dla których opis hamiltonowski jest nieadekwatny.

W mechanice klasycznej jeżeli równania ruchu są niezmiennicze ze względu na przesunięcia w czasie

to siła F lub potencjał U nie może jawnie zależeć od czasu

Konsekwencją równań Hamiltona (patrz mechanika klasyczna) jest stałość energii (hamiltonianu), bo:

Tak więc zachowana jest wielkość

Symetria translacji w czasie jest szczególnym przypadkiem ogólniejszej symetrii związanej z niezmienniczością mechaniki klasycznej względem transformacji Galileusza

Transformacje te tworzą grupę Galileusza. W szczególnej teorii względności zachowanie energii jest również konsekwencją translacji w czasoprzestrzeni Minkowskiego

Pamietając, że x⁰ = ct, przypadek dla μ=0 odpowiada translacji czasu.

Konsekwencją symetrii translacji w czasoprzestrzeni Minkowskiego jest zachowanie tensora energii - pędu.

Z zasady zachowania energii wynika kilka innych zasad między innymi: Pierwsza zasada termodynamiki, zasada zachowania energii mechanicznej.

Zasada zachowania pędu

Zmiana pędu następuje w wyniku działania na ciało siły przez pewien czas. Iloczyn siły i czasu jej działania nazywany jest popędem siły (I)

Jeżeli w układzie inercjalnym na ciało (układ ciał) nie działa siła, lub działające siły równoważą się:

to całkowity pęd ciała (układu ciał) nie zmienia się:

Powyższe zdanie stanowi treść zasady zachowania pędu. Zasada zachowania pędu jest konsekwencją symetrii translacji w przestrzeni (twierdzenie Noether)

Jeżeli energia potencjalna jest niezmiennicza ze względu na translację,

to

czyli na ciało nie działa żadna siła i w konsekwencji pęd układu jest zachowany.

Zderzenie sprężyste, zderzenie elastyczne, jest to zderzenie, w którym w stanie końcowym mamy te same cząstki (obiekty) co w stanie początkowym i zachowana jest energia kinetyczna. W fizyce zderzenia analizuje się opisując stan ciał przed i po zderzeniu nie wnikając w szczegóły oddziaływania w trakcie zderzenia. Zderzenie, w którym energia kinetyczna nie jest zachowana nazywa się zderzeniem niesprężystym. Przykładami zderzeń sprężystych mogą być: zderzenia cząsteczek gazu doskonałego, zderzenia elektronów, rozproszenie niskoenergetycznej cząstki alfa na jądrze atomowym (eksperyment Rutherforda) i wiele innych z mikroświata. Zderzenia zachodzące w skali makroskopowej są sprężyste w pewnym przybliżeniu, np. stosowane jako przykład zderzenie sztywnych stalowych kul jest tylko w przybliżeniu zderzeniem sprężystym, niewielka część energii kinetycznej jest bowiem zawsze tracona, np. w formie wydzielanego ciepła i fali akustycznej wytwarzanych w chwili zderzenia. Zazwyczaj za zderzenia uznaje się procesy trwające bardzo krótko, choć niektóre procesy przebiegające bardzo długo jak przejście komety poruszającej się z prędkością hiperboliczną w okolicy Słońca, z odchyleniem jej toru, też może być rozpatrywane jako oddziaływanie sprężyste.

Zderzenie całkowicie niesprężyste, zderzenie doskonale nieelastyczne - zderzenie, w którym następuje największa możliwa strata energii kinetycznej, tj. zderzenie, którego produkty mają najmniejszą możliwą energię kinetyczną umożliwiającą im spełnienie zasady zachowania pędu. Wygodnie jest analizować takie zderzenie w układzie środka masy zderzających się obiektów. W układzie tym całkowity pęd wynosi zero. Oznacza to, że minimalna energia kinetyczna po zderzeniu też może być zerowa, sytuacja ta odpowiada stanowi spoczynku wszystkich produktów zderzenia. Ponieważ jednak strata energii nie może zależeć od układu odniesienia, dochodzimy do wniosku, że w dowolnym układzie odniesienia wszystkie produkty zderzenia całkowicie niesprężystego poruszają się z tą samą prędkością w tym samym kierunku. Dla zderzeń obiektów makroskopowych oznacza to, że po zderzeniu ciała te poruszają się z takimi samymi prędkościami, tak jakby stanowiły jeden obiekt. Kosztem traconej energii kinetycznej wykonywana jest praca związana z odkształceniem ciał i rośnie ich energia wewnętrzna (wydziela się w postaci ciepła .

II. Metodologia wykonania pomiarów

Na rys. 3 pokazany jest schemat układu pomiarowego.

Rys. 3. Schemat układu pomiarowego do zderzenia kul

Kolejność pomiarów:

1. Na nakrętki zawieszek wkręcić dwie kule wskazane przez prowadzącego zajęcia, zwrócić uwagę czy układ jest wypoziomowany.

2. Kręcąc pokrętłem 7 umieszczonym na wsporniku górnym ustawić taką odległość między nitkami 10, aby kule stykały się ze sobą.

3. Poluzować śruby 9 i przesunąć uchwyty 8 do pozycji, w której ostrza zawieszek będą znajdować się w jednej płaszczyźnie z kątownikami ze stali 3; dokręcić śruby 9.

4. Skorygować centralne ustawienie kul doprowadzając do równości poziomów rys na kulach.

5. Ustawić kątowniki tak, aby ostrza zawieszek przy początkowym położeniu kul wskazywały kąt
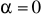
   (regulacja odpowiednimi śrubami na kątowniku).

6. Ustawić elektromagnes w odległości wskazanej przez prowadzącego i na takiej wysokości, aby jego oś była przedłużeniem rys na skali (regulacja śrubami 4 i 5).

7. Włączyć przyrząd do sieci przyciskiem W1.

8. Nacisnąć przełącznik W3.

9. Pokrętłem 6 ustawić położenie elektromagnesu tak, trzymał on kulę w pozycji odchylonej.

10. Prawą kulę odciągnąć w stronę elektromagnesu i zablokować w tym położeniu, lewą ustawić nieruchomą w położeniu spoczynkowym.

11. Odczytać kąt
    .

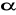
12. Wcisnąć przełącznik W2.

13. Po zderzeniu kul zaobserwować, na jakie odległości kątowe
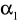
    i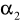
    odbijają się kule. Zwrócić uwagę czy zderzenie jest centralne. Jeżeli nie, powtórzyć regulację opisaną w punktach 3÷5. Pomiary powtórzyć 10 razy.

14. Dokonać pomiaru długości zawieszenia kul rozumianą jako najkrótszą odległość między prętem wspornika górnego a środkiem kul, oraz na wadze analitycznej wyznaczyć masy
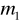
    i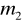
    kul wraz z zawieszkami. Masa wieszaczka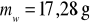
    .

15. Pomiary powtórzyć dla innego zestawu kul.

16. Wykonać analogiczne pomiary dla zderzeń niesprężystych. W tym celu należy nakleić na jedną z kul niewielki plasterek plasteliny w miejscu zderzenia się z drugą kulą.

Tabela pomiarowa dla zderzeń sprężystych

							l
[ º ]	[ º ]	[ º ]	[ º ]	[ º ]	[ º ]	[ º ]	[ cm ]
15	2,75	2,68	0,15	12	12,5	0,16	48
15	2,25								12
15	2,25								13,25
15	2								12
15	3								12,75
15	2,5								12,75
15	2,5								12
15	3,2								12,75
15	3,25								12,75
15	3								12,5

u (x) =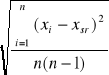

u (α_1max) =

u (α_{2 max}) =
0,16

u (α) =
= 0,14

u (l) =
= 0,12

u (m) =
= 0,06

Tabela pomiarowa dla zderzeń niesprężystych

				l
[ º ]	[ º ]	[ º ]	[ º ]	[ cm ]
15	6,25	6,625	0,08	48
15	6,5
15	6,5
15	6,25
15	7
15	6,5
15	7
15	6,75
15	6,25
15	7

u (x) =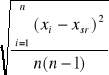

u (α_max) =
0,08

III. Obliczenia

I - zderzenia sprężyste m₁ = 112 g m₂ = 105 g m₁ ` = 129,28 g m<sub>2</sub> ` = 122,28 g

II - zderzenia niesprężyste m₁ = 112 g m₂ = 107 g m₁ ` = 129,28 g m<sub>2</sub> ` = 124,28 g

Zderzenia sprężyste

E_pocz = m_1'* g * l ( 1 - cos α ) = 0,12928 * 10 * 1,759 = 1,085 J

p_pocz = m_1'
= 0,12928
= 0,533 kg m/s

E_konc = m_1'* g * l ( 1 - cos α₁ ) + m_2'* g * l ( 1 - cos α₂ ) = 0,12928 * 10 * 0,48 * 1,895 +

0,12228 * 10 * 0,48 * 0,002 = 1,169 J

p_konc = m_1'
- m_2'
= 0,12928

+ 0,12228
= 0,534 kg m/s

Zderzenia niesprężyste

E_pocz = m_1'* g * l ( 1 - cos α ) = 0,12928 * 10 * 0,48 * 1,759 = 1,085 J

p_pocz = m_1'
= 0,12928
= 0,533 kg m/s

E_konc =( m₁' + m₂ `) * g * l * (1 - cos α' ) = ( 0,12928 + 0,12428 ) *10* 0,48 * 0,056 = 0,067 J

p_konc = ( m₁' + m₂ `)
= ( 0,12928 + 0,12428 )
=

= 0,182 kg m/s

Zadanie	Epocz	Ekonc	ppocz	pkonc
-	[J]	[J]	[kg m/s]	[kg m/s]
I	1,085	1,169	0,533	0,534
II	1,085	0,067	0,533	0,182

u(E_p) =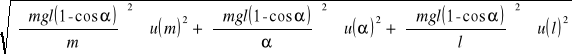
=

=

u( p_p) =

=

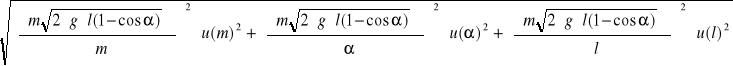
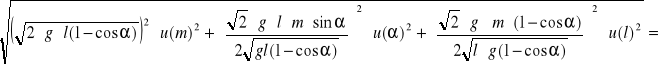
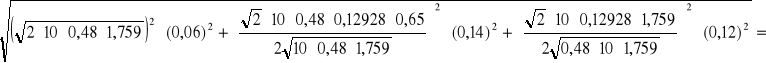
=0,071

u(E_k) =

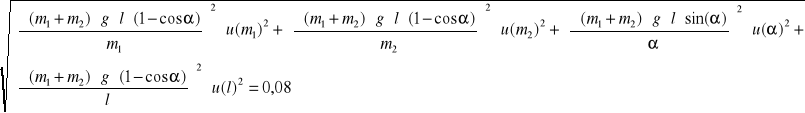
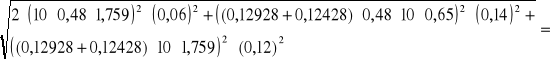
0,0097

u (p_k) =

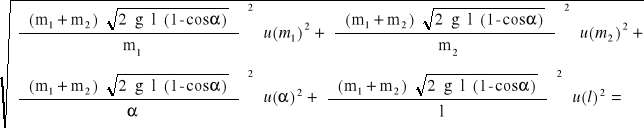
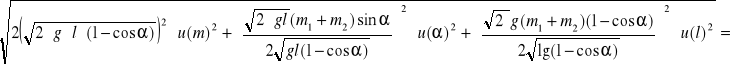
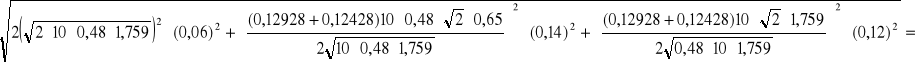
0,038

Dla zderzeń niesprężystych:

u(E_k) =

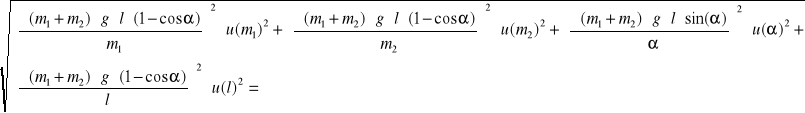
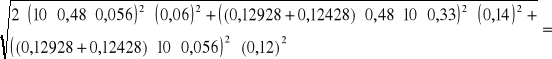
_0,061

u (p_k) =

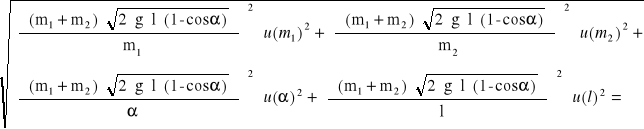
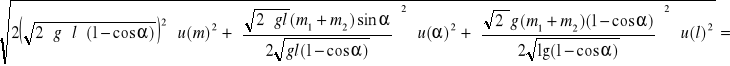
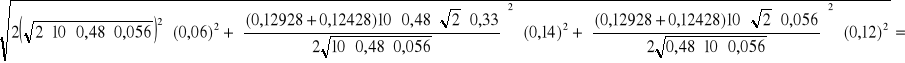
0,092

Wyniki wraz z niepewnością:

zderzenia sprężyste

E_p = 1,091 ± 0,057 J

p_p = 0,531 ± 0,071 kg m/s

E_k = 1,177 ± 0,08 J

p_k = 0,533 ± 0,038 kg m/s

zderzenia niesprężyste

E_p = 1,091 ± 0,058 J

p_p = 0,531 ± 0,071 kg m/s

E_k = 0,068 ± 0,061J

p_k = 0,184 ± 0,092kg m/s

Wnioski :

Stwierdzam iż zasada zachowania energii i pędu została spełniona dla zderzeń sprężystych, ponieważ energia początkowa równa jest sumie energii końcowych, i również pęd początkowy równy jest pędowi końcowemu. Dla zderzeń niesprężystych, energia początkowa nie powinna się równać energii końcowej, i tak otrzymaliśmy, a pęd początkowy powinien się równać pędowi końcowemu, a nieco odbiega od tego. Dlatego zasada zachowania pędu dla zderzeń niesprężystych nie została zachowana.

---