Wpływ temperatury, energii aktywacji, szybkości ścinania, naprężenia ścinającego, stężenia substancji na lepkośc

1. Temperatura: Dla większości cieczy lepkość maleje ze wzrostem temperatury

--> η = A * e ^{Wa/ kT}

gdzie:

• A - współczynnik proporcjonalności

• Wa - energia aktywacji lepkosci

• k - stała Boltzmanna

• T - temperatura bezwzgledna cieczy

Krew - lepkosć zwiększa się z obniżeniem temp (0^o C - 2,5 razy wieksza niż przy 37^o C) - zmiany podobne do wody - lekosć względna nie zależy od temperatury.

2. Energia aktywacji:

Założenie teorii lepkości cieczy - kazda czesteczka zajmuje położenie równowagi --> przejście jej w kierunku przepływu możliwe - gdy uzyska energię aktywacji lepkości (Wa)

Względna liczba cząsteczek majacych w danej temp energię aktywacji

--> Δn_a/n = e ^-Wa/kT

Wzrost temp cieczy --> wzrost predkości --> wzrost energii bezładnego ruchu cząsteczek --> wzrost wzglednej liczby czasteczek majacych energię większą od en aktywacji.

Po zlogarytmowaniu poprzedniego równania:

--> ln η = ln A +Wa/k * 1/T

wykres - linia prosta - wyznaczenie en aktywacji i współczynnika A.

3. Prędkość scinania - lepkość pozorna krwi - funkcja malejąca predkosci ścinania.

( przy 37^o C i hematokrycie 45% i szybkości ścinania 0,1 s^-1 --> 100mPas, przy 230 s^-1 --> spadek do 4mPas).

Powody:

• agregacja krwinek czerwonych przy małych prędkościach ścinania

• deformacja i ukierunkowanie erytrocytów przy dużych predkościach ścinania

Wzrost pedkości ścinania - maleje agregacja --> maleje lepkosć krwi

Przy prędkościach > 150- 200 s^-1 - deformacja erytrocytów - zmniejszenie lepkości krwi - z powodu zmniejszenia oddziaływan hydrodynamicznych.

3. Stężenie (nie wiem czy to jest dobrze, bo to wynika tylko z mojej interpretacji wzoru, nie znalazlem tego gdzie indziej, jak to znajdziecie, dajcie mi koniecznie znać! )

Lepkość rośnie ze wzrostem stężenia, bo:

η/η_o = 1 + 2,5 Φ (wzór Einsteina na lepkosć wzgledną r-ru)

Φ = c * N_A * v / M

gdzie:

• Φ - objętościowy współczynnik r-ru

• c - stężenie r-ru

• M - masa molowa

• N_A - l. Avogadra

• v - objętość 1 cząstki

2.Właściwości reologiczne krwi

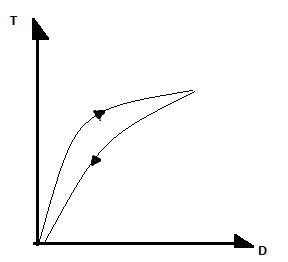
Krew jest cieczą nienewtonowską o charakterze pseudoplastycznym i tiksotropowym. Jej nienewtonowski charakter polega na tym, że stosunek naprężenia ścinającego do gradientu prędkości w danych warunkach ciśnienia i temperatury dla danej cieczy nie jest stały. Jeśli maleje on monotonicznie wraz ze wzrostem gradientu prędkości i nie zależy od czasu i sposobu ścinania, to mówimy o cieczy pseudoplastycznej. Jeśli stosunek ten zależy nie tylko od szybkości, ale też od czasu i sposobu ścinania, to ciecz nazywamy tiksotropową. Dla cieczy tiksotropowych krzywa płynięcia wykazuje histerezę.

Właściwości tiksotropowe krwi są związane z tworzeniem struktur w warunkach braku ścinania oraz ich rozpadaniem się w obecności naprężeń ścinających. Strukturami tymi są skupiska krwinek czerwonych; ich tworzenie się nazywamy agregacją.

Odtwarzanie struktur odbywa się w bardzo krótkim czasie, więc histereza krzywej płynięcia krwi jest prawie niezauważalna.

3.Krzywa płynięcia krwi

Przepływ cieczy lepkiej możemy traktować jako jeden ze specjalnych przypadków odkształcenia postaci materii. Oddziaływania występujące w przepływających płynach można scharakteryzować, podając naprężenia styczne (Τ=F/S) jako funkcję prędkości ścinania (u=dv/dx). Wykres zależności Τ=f(u) nazywamy krzywą płynięcia; na jej podstawie różnicujemy płyny na:

2. newtonowskie- wykresem jest linia prosta przechodząca przez początek układu współrzędnych

3. nienewtonowskie- wykresem jest linia prosta, która nie przechodzi przez początek układu współrzędnych.

Podział ten stosujemy dla ustalonych warunków ciśnienia i temperatury. Wartość ilorazu Τ/u nazywamy lepkością płynu. (η).

5. Krzywa pozornej lepkości krwi od prędkości ścinania, wartości przykładowe.

Lepkość pozorna krwi maleje wraz ze wzrostem prędkości ścinania. Przy temperaturze 37stopni C i hematokrycie 45% oraz prędkości ścinania 0,1 1/s wynosi 100mPas. Wzrost prędkości ścinania do 230 1/s powoduje spadek lepkości pozornej do około 4mPas.

Zależność ta wynika z dwóch zjawisk:

-agregacji erytrocytów(główny czynnik dla małych prędkości ścinania)

-deformacji i ukierunowaniu erytrocytów(główny czynnik dla dużych prędkości ścinania)

Wysoka prędkość ścinania prowadzi do zmniejszenia stopnia agregacji erytrocytów, a tym samym do spadku lepkości cieczy.

Przy prędkości ścinania około 150mPas-200mPas dochodzi do zjawiska deformacji erytrocytów i również spadku lepkosci w skutek zmniejszenia odzialywań hydrodynamicznych.

WYKRES- s.640 JAROSZYK 18.19

4.Prawo Ostwalda

Prawo dysocjacji Ostwalda nie pauje ni chuj do tematu! Skłaniam się ku temu, że chodzi tu o wyprowadzenie wzoru na lepkość względną w wiskozymetrze Ostwalda.

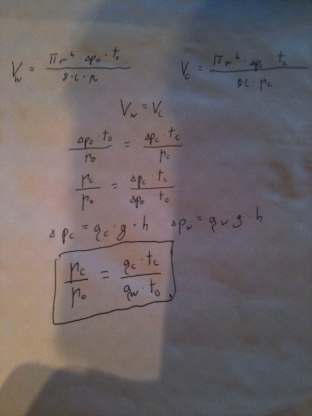
6. Równanie Cassona + Granica Płynięcia

Granica płynięcia - naprężenie powyżej którego krew dopiero zaczyna płynąć.

Krew - posiada granicę płynięcia - ale trudna do oznaczenia - przyczyny metodyczne.

Określenie granicy --> przy pomocy reologicznego modelu Cassona - wyraża w sposób analityczny krzywą płynięcia krwi

τ^½ = τ₀^½ + k_c * D^{½ <-- równanie Cassona}

gdzie:

4. τ - naprężenie ścinające (styczne do powierzchni)

5. D - szybkość ścinania

6. τ_{0 -} granica płynięcia

7. k_{c -} współczynnik konsystencji

Według dotychczasowych badań - granica płyniecia krwi ~5mPa.

Wpływ na jej wartość maja:

• hematokryt

• -stężenie fibrynogenu i innych składników białkowych osocza

Wyznaczanie granicy płyniecia - ekstrapolacja krzywej płynięcia do prędkości równej 0.

Przykładowa krzywa płyniecia krwi w układzie pierwiastkowym dla krwi prawidłowej i krwi chorych na miażdżycę zarostową kończyn dolnych znajdziecie na stronie 600 Jaroszyka (rozdział 18.6.1 ryc 18.18)

7.

Elastyczność erytrocytów, która związana jest z ich zdolnością do odkształcania, powoduje większą lepkość krwi. Wysokie prędkości ścinania, które powodują zmniejszenie odkształcalności (ale zwiększenie odkształcenia…), są przyczyną spadku lepkości.

Zdolność erytrocytów do odkształcania wiąże się z:

8. Brakiem jądra

9. Małą lepkością cytoplazmy

10. Korzystnymi właściwościami lepko-sprężystymi błony

11. Dużą wartością stosunku powierzchni swobodnej do objętości

Zmniejszona odkształcalność krwi jest przyczyną wielu chorób.

9.

Największy wpływ na lepkość krwi przy stałym hematokrycie i małych prędkościach ścinania ma zjawisko agregacji krwinek czerwonych.

Im silniejsza agregacja tym większa lepkość krwi.

Im większa prędkość ścinania tym mniejsza agregacja

Przy prędkościach ścinania powyżej 150-200 s^-1 występuje zjawisko deformacji krwinek czerwonych, co powoduje mniejszą lepkość wskutek zmniejszenia oddziaływań hydrodynamicznych.

11.Wiskozymetr Ubbelohde'a,

Pomiar lepkość względnej roztworów potrzebne do sporządzenia wykresu zależności lepkość właściwej od stężenia przeprowadzamy stosując wiskozymetr kapilarny Ubbelohde'a. Jego działanie jest oparte na prawie Poiseuila'e(strona 98 Kędzia).

Pomiar lepkości względnej cieczy polega na mierzeniu czasu t0 (zero) przepływy przez kapilarę wiskozymetru cieczy wzorcowej o objętości zawartej pomiędzy kreskami A i B oraz czasu t przepływu przez kapilarę cieczy badanej o tej samej objętości. Opierając na prawie Poiseuila'e oraz uwzgleniajac że objętości cieczy badanej i wzorcowej są równe, możemy zapisać:

(strona 105 Kędzia; wzór jest bez numeru),

następnie po przekształceniu powstania nam

(wzór 10.8; ta sama strona).

Dzięki swojej konstrukcji wiskozymetr zapewnia że na końcu kapilary podczas pomiarów tworzy się „wiszący poziom” dzięki czemu Δp powodujące przepływ cieczy nie zależy od ilości cieczy znajdującej się w wiskozymetrze, a także od napięcia powierzchniowego cieczy.

Δp jest to ciśnienie hydrostatyczne:

(Δp=ρ*g*h, Δp0(zero)=ρ0*g*h)

Ostateczny wzór na wyliczenie lepkości względnej przy pomiarach tym wiskozymetrem ma postać:

(wzór 10.9 strona ta sama)

jeśli gęstość cieczy badanej do wzorcowej są podobne można je nie umieszczać we

wzorze

(wzór 10.10)

Obu wzorów możemy wysnuć wniosek że do policzenia lepkości względnej potrzebny jest nam czas przepływu cieczy badanej i wzorcowej.

Wybaczcie brak wzorów ale nie posiadam ani skanera anie aparatu.

Na dole jest model wiskozymetru jaki znalazłam na necie.

13.Wiskozymetr Ostwalda

Jest urządzeniem służącym do pomiaru lepkości względnej

Polega na mierzeniu czasu t zero przepływu przez kapilarę wiskozymetru cieczy wzorcowej o konkretnej objętości ( zawartej pomiędzy punktami A i B) oraz czasu przepływu przez kapilarę cieczy badanej o tej samej objętości

Możemy ją wyliczyć ze wzoru:

Można go otrzymać z zapisanego dwukrotnie Prawa Pouseulle'a dla cieczy wzorcowej i dla cieczy badanej oraz porównując strony tych równań.

12.Wiskozymetr rotacyjny

Jest urządzeniem służącym do badań cieczy nienewtonowskich i określania krzywej płynięcia czyli zależności naprężenia ścinającego od szybkości ścinania (D).

Wartość
obliczamy ze wzoru:

gdzie:

to lepkość pozorna dla badanej cieczy przy rosnących i malejących szybkościach ścinania.

D to szybkość ścinania

Wartości kolejnych naprężeń ścinajacych możemy obliczyc ze wzoru:

(Z odczytujemy z odpowiednich tabel dołączonych do wiskozymetru).

14. Wiskozymetryczny pomiar masy cząsteczkowej biopolimeru.

Ustaloną na podstawie doświadczeń zależność granicznej liczby lepkościowej roztworu polimeru od jego masy cząsteczkowej przedstawia wzór :

[η] = K × M^α

gdzie: K-stała zależna od rodzaju polimeru i rozpuszczalnika

α - współczynnik zależny od kształtu makrocząsteczki polimeru w roztworze

Wartość stałych K i są określane na podstawie pomiaru masy molowej polimeru metodą rozpraszania światła lub metodą sedymentacji.

Po zlogarytmowaniu wyżej wymienionego wzoru otrzymujemy:

Log M=1/α (log[η]-logK)

Wiskozymetryczny pomiar masy cząsteczkowej polega na wyznaczeniu granicznej liczby lepkościowej roztworu badanego polimeru ([η]=lim η_wł/c) i wyliczeniu masy cząsteczkowej z wyżej wymienionego wzoru.

15. Metoda Stockesa

Metoda Stockesa polega na pomiarze prędkości opadania kulki w badanej cieczy. Na kulkę działają 3 siły:

12. siła ciężkości skierowana pionowo w dół, wyrażana wzorem

P = m*g = V*ρ*g = ⁴/₃ πr³ *ρ *g

• siła wyporu hydrostatycznego skierowana do góry, wyrażana prawem Archimedesa

Q = V* ρ_c*g = ⁴/₃ πr³ * ρ_c*g

4. siła tarcia wewnętrznego ( oporu lepkości ), skierowana ku górze, wyrażana prawem Stockesa

R = 6πr*η*v

gdzie: Q R

m-masa kulki

V-objętośc kulki h

g-przyspieszenie ziemskie

ρ_c-gęstośc cieczy P

ρ-gęstośc kulki

r-promień kulki

η-lepkośc cieczy

v-prędkośc kulki

Początkowo kulka opada ruchem przyspieszonym, gdyż siła ciężkości kulki jest większa od sumy sił wyporu i lepkości. Zgodnie ze wzorem Stockesa, wzrost prędkości (v) kulki powoduje wzrost sily lepkości (R). Przy odpowiednio wysokiej prędkości zachodzi równośc:

P = Q + R

Od tej chwili kulka porusza się ruchem jednostajnym ze stałą prędkością. Podstawiając odpowiednie wartości sił do powyższego wzoru otrzymamy:

⁴/₃ πr³ *ρ *g = ⁴/₃ πr³ * ρ_c*g + 6πr*η*v

po przekształceniu otrzymamy:

η = 2r² * g( ρ - ρ_c ) / 9v

Prędkośc opadania kulki otrzymujemy z czasu opadania kulki (t) i długości przedziału w którym ten czas mierzymy (h).

16. Rodzaje Lepkości

Lepkośc możemy wyliczyc z prawa Newtona ( patrz pytanie nr 17 ):

η = ( F*Δx)/(S*Δv)

Jest to siła niezbędna do utrzymania różnicy prędkości 1 m/s między dwiema warstwami cieczy o powierzchni 1 m², przesuwającymi się względem siebie w odległości 1m. Jednostką lepkości jest N*s/ m², używana jest też jednostka zwana puazem:

P = 0,1 N*s/ m²

Lepkośc względna to stosunek lepkości danej cieczy do lepkości cieczy wzorcowej w najczęstszym przypadku wody, a w przypadku roztworu jest do lepkości czystego rozpuszczalnika. Jest wielkością bezwymiarową.

[ η'] = η/ η₀

Lepkośc właściwa także jest wielkością bezwymiarową definiowaną wzorem:

η_wł = η/ η_{0 -} 1

Stosunek lepkości właściwej do stężenia (c) rozpuszczonego składnika przy tymże stężeniu dążącym do zera i prędkości ścinania (u) dążącej do zera, nazywamy lepkością graniczną:

[η] = lim_{c-->0 u-->0} (η_wł/c)

Jednostką granicznej liczby lepkościowej jest cm³/g ( odwrotnośc stężenia ).

Wartości granicznej liczby lepkościowej odczytujemy z wykresu funkcji η_wł/c = f (c) poprzez ekstrapolację otrzymanej prostej do stężenia zerowego :)

η_wł/c

0 c

Posiadając wartośc granicznej liczby lepkościowej możemy wyliczyc masę dowolnych biopolimerów ( patrz pytanie 14 ).

---