Politechnika Lubelska w Lublinie
Laboratorium elektrotechniki		Ćwiczenie nr: 8
Nożyński Paweł Ochnik Piotr Smyk Elżbieta Szpakowski Marek	Semestr: II	Grupa: EDi. 2.1	Rok akadem.: 2002/2003
Temat: Stany nieustalone w obwodach z elementami RC		Data wykonania: 18.03.03	Ocena:

Schemat pomiarowy:

Dobór przyrządów:

V₁ - Woltomierze LM - 3,

V₂ -Digitalvolmeter V240 (o rezystancji R_V =14 MΩ)

Zasilanie z tablicy 5V

1. Ładowanie kondensatora

C1=40μF R1=1MΩ					C2=20μF R2=3.3MΩ
t	U	uc	uR	i	t	U	uc	uR	i
s	V	V	V	μA	s	V	V	V	μA
3	2.6	0,21	2,39	2,39	3	2.6	0,12	2,48	0,75
6			0,38	2,22	2,22		6		0,24	2,36	0,71
9			0,56	2,04	2,04		9		0,35	2,25	0,68
12			0,72	1,88	1,88		12		0,47	2,13	0,64
15			0,89	1,71	1,71		15		0,59	2,01	0,6
18			1,01	1,59	1,59		18		0,68	1,92	0,58
21			1,14	1,46	1,46		21		0,77	1,83	0,55
24			1,26	1,34	1,34		24		0,86	1,74	0,52
27			1,37	1,23	1,23		27		0,94	1,66	0,5
30			1,48	1,12	1,12		30		1,01	1,59	0,48
33			1,56	1,04	1,04		33		1,09	1,51	0,45
36			1,65	0,95	0,95		38		1,19	1,41	0,42
39			1,74	0,86	0,86		43		1,28	1,32	0,4
42			1,8	0,8	0,8		48		1,39	1,21	0,36
45			1,85	0,75	0,75		53		1,46	1,14	0,34
50			1,94	0,66	0,66		58		1,55	1,05	0,31
55			2,04	0,56	0,56		63		1,63	0,97	0,29
60			2,11	0,49	0,49		68		1,7	0,9	0,27
65			2,13	0,47	0,47		73		1,77	0,83	0,25
73			2,22	0,38	0,38		81		1,87	0,73	0,22
81			2,27	0,33	0,33		89		1,95	0,65	0,19
89			2,35	0,25	0,25		97		2,02	0,58	0,17
97			2,39	0,21	0,21		107		2,09	0,51	0,15
105			2,42	0,18	0,18		117		2,16	0,44	0,13
113			2,44	0,16	0,16		127		2,22	0,38	0,11
121			2,48	0,12	0,12		137		2,26	0,34	0,1
					152			2,33	0,27	0,08
167		2,38	0,22	0,06
187		2,44	0,16	0,04
207		2,48	0,12	0,03
237		2,53	0,07	0,02
267		2,56	0,04	0,01

Wzory i przykładowe obliczenia:

s - teoretyczna stała czasowa 1

s- teoretyczna stała czasowa 2

0,21=2,39

Charakterystyki u_C = f(t), u_R = f(t), i = f(t) dla C = 40 μF i R₁ = 1 MΩ

Charakterystyki u_C = f(t), u_R = f(t), i = f(t) dla C = 20 μF i R₂ = 3,3 MΩ

2. Rozładowanie kondensatora

C1=40μF R1=1MΩ			C2=20μF R2=3.3MΩ
t	uc	i	t	uc	i
s	V	μA	s	V	μA
3	2,64	-2,64	3	2,52	-0,76
6	2,48	-2,48	6	2,39	-0,72
9	2,26	-2,26	9	2,25	-0,68
12	2,07	-2,07	12	2,1	-0,63
15	1,87	-1,87	15	1,97	-0,59
18	1,77	-1,77	18	1,85	-0,56
21	1,62	-1,62	21	1,75	-0,53
24	1,49	-1,49	24	1,65	-0,5
27	1,34	-1,34	27	1,55	-0,46
30	1,22	-1,22	30	1,46	-0,44
33	1,12	-1,12	33	1,36	-0,41
36	1,03	-1,03	36	1,26	-0,38
39	0,93	-0,93	39	1,17	-0,35
42	0,85	-0,85	42	1,09	-0,33
45	0,77	-0,77	45	1,01	-0,3
50	0,66	-0,66	48	0,95	-0,28
60	0,57	-0,57	53	0,89	-0,26
65	0,5	-0,5	58	0,81	-0,24
70	0,43	-0,43	63	0,75	-0,22
78	0,34	-0,34	68	0,69	-0,2
86	0,27	-0,27	76	0,6	-0,18
94	0,22	-0,22	84	0,52	-0,15
102	0,17	-0,17	92	0,46	-0,13
110	0,14	-0,14	100	0,41	-0,12
118	0,11	-0,11	110	0,34	-0,1
128	0,08	-0,08	120	0,29	-0,08
138	0,06	-0,06	130	0,24	-0,07
153	0,03	-0,03	145	0,19	-0,05
168	0,02	-0,02	160	0,15	-0,04
188	0	0	180	0,11	-0,03
			200	0,08	-0,02
						220	0,06	-0,01
						250	0,03	-0,009
						280	0	0

C=18 μF, RV=14 MΩ, R1=0,91 MΩ, τ1 = 15,38s			C=18 μF RV=14 MΩ R2=2MΩ τ2 =31,5 s
t	uc	i	t	uc	i
s	V	μA	s	V	μA
0	4,307	-5,041	0	3,982	-2,275
16	2,863	-3,347	34	1,502	-0,858
32	0,810	-0,948	68	0,623	-0,356
48	0,366	-0,428	102	0,266	-0,152
64	0,158	-0,185	136	0,107	-0,061
80	0,049	-0,057	170	0,030	-0,017
96	0,029	-0,034	204	0,011	-0,006
112	0,016	-0,019

Wzory i obliczenia

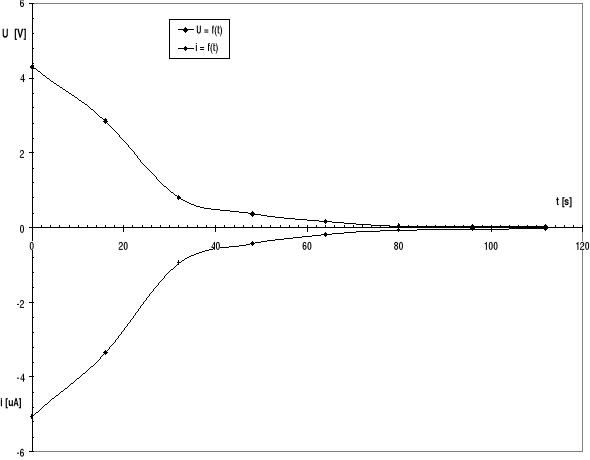
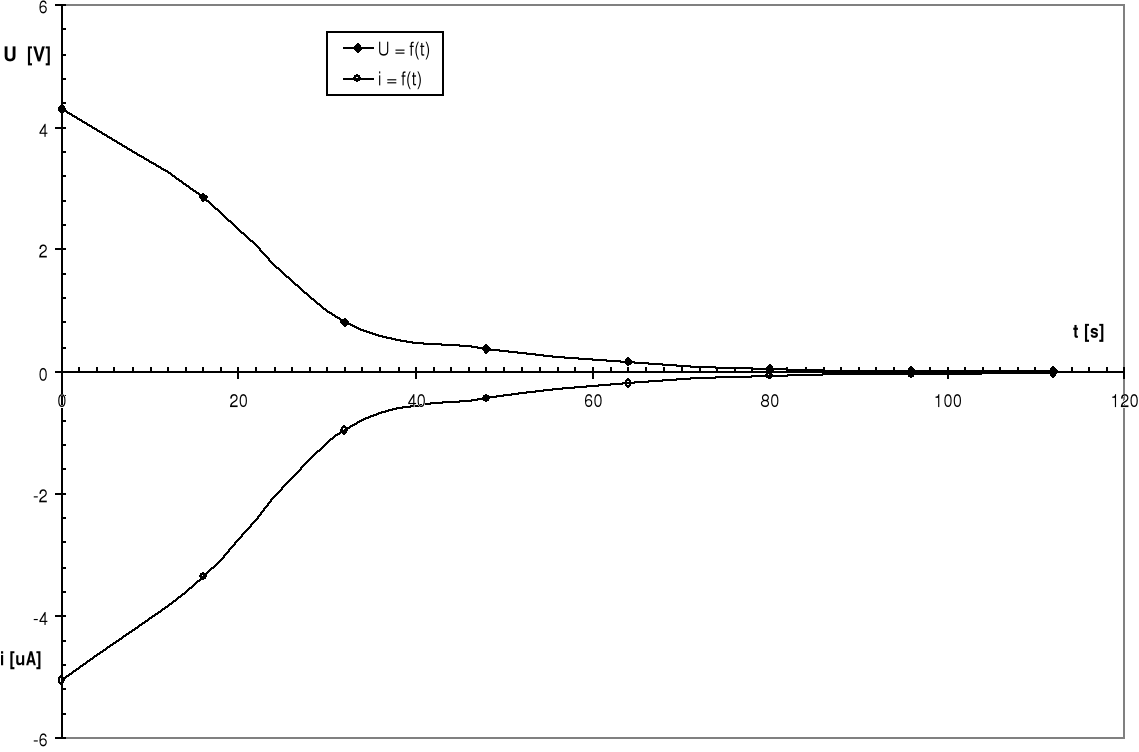
Charakterystyki u_C = f(t), i = f(t) dla C = 18 μF i R₁ = 0,91 MΩ, R_V=14 MΩ

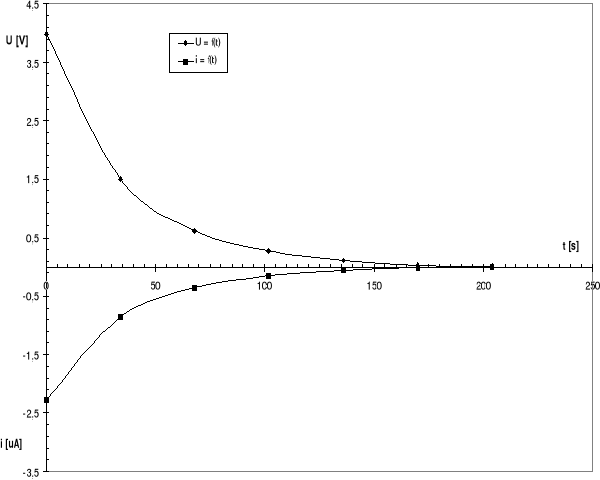
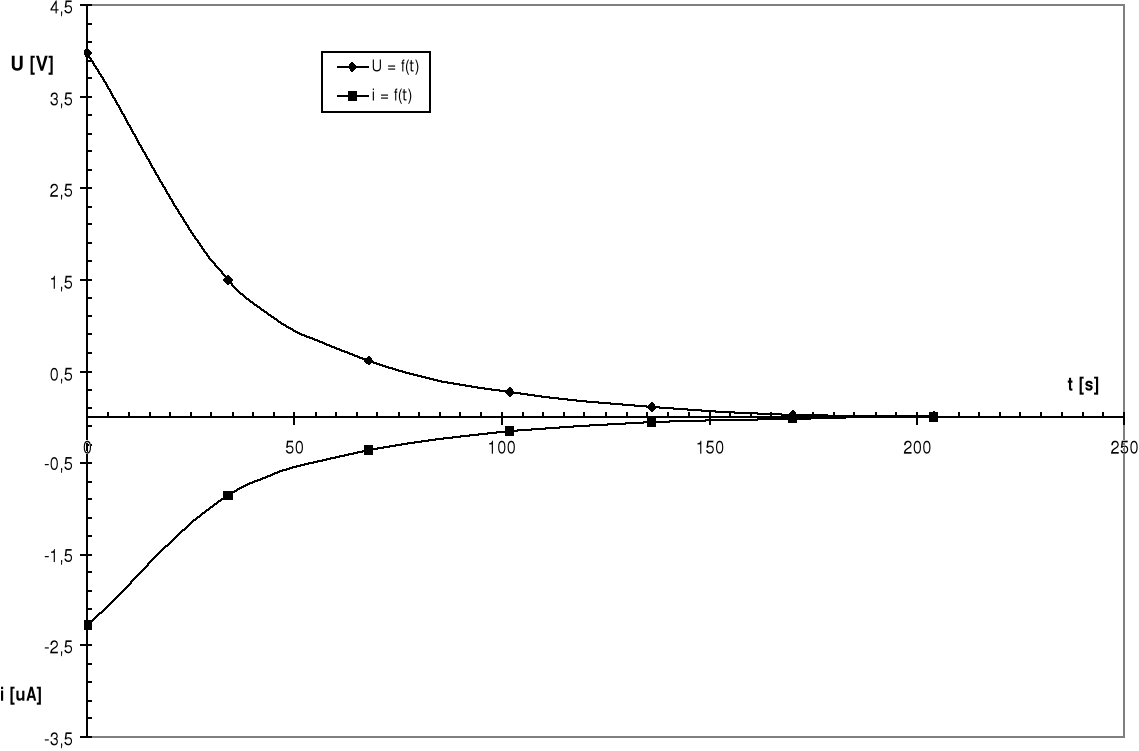
Charakterystyki u_C = f(t), i = f(t) dla C = 18 μF i R₂ = 2 MΩ, R_V=14 MΩ

Wnioski

W ćwiczeniu woltomierz mierzący napięcie na kondensatorze był podłączony na stałe i jako element nie idealny posiada skończoną rezystancje (14MΩ), która została uwzględniona w obliczeniach.

Krzywe ładowania i rozładowania kondensatora otrzymane doświadczalnie zgadzają się z teoretycznymi przebiegami krzywej wykładniczej.

Czas ładowania jak i rozładowania zgodnie z teorią rośnie wraz ze wzrostem stałej czasowej τ (czyli wraz ze wzrostem wartości elementów R i C).

---