111 (4)

WYDZIAŁ TRANSPORTU

ZADANIA POWTÓRZENIOWE PRZED PIERWSZYM KOLOKWIUM Z PROBABILISTYKI

1.    Studenci stwierdzili, że prawdopodobieństwo zdania egzaminu z Probabilistyki w pierwszym terminie wynosi 0,4, natomiast prawdopodobieństwo zdania egzaminu z Fizyki w pierwszym terminie wynosi 0,7, przy czym zdarzenia te są. niezależne. .Jakie jest prawdopodobieństwo zdania przynajmniej jednego z tych egzaminów w pierwszym terminie?

2.    Firma komputerowa przeprowadziła sondaż w urzędach gminnych, którego celem było zbadanie zainteresowania nową wersją programu biurowego. 80% respondentów wykazało chęć kupna nowej wersji programu. Spośród urzędów zainteresowanych kupnem nowej wersji programu 40% wyraziło chęć modernizacji komputerów. Oblicz prawdopodobieństwotego, że losowo wybrany urząd gminny planuje modernizację komputerów i chce kupić nową wersję programu biurowego.

3.    Obliczyć prawdopodobieństwo przekazania sygnału przez poniższy układ 6 działających niezależnie przekaźników (niezawodności poszczególnych przekaźników pokazano na rysunku).

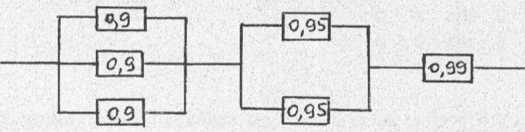
4.    Zaopatrzenie rynku w ubiory ochronne pokrywają trzy fabryki, przy czym fabryka A w 45%, fabryka B w 20% a resztę pokrywa fabryka C. Gatunek I stanowi 80% produkcji fabryki A, 65% produkcji fabryki B i 90% produkcji fabryki C. Pozostałe ubiory ochronne są II gatunku, (a) Jakie jest prawdopodobieństwo, że losowo wzięty ubiór ochronny jest I gatunku? (b) Jakie jest prawdopodobieństwo, że zakupiony ubiór II gatunku pochodzi z fabryki C?

5.    Gdy pani Edyta wyjeżdża na konferencję prosi zawsze sąsiadkę, aby ta podczas nieobecności w domu podlewała jej kwiaty. Jest to konieczne, gdyż prawdopodobieństwo tego, że nie podlewane przez czas trwania konferencji kwiaty zwiędną wynosi 0,8. Może się też zdążyć, że kwiaty - mimo podlewania - nie doczekają przyjazdu właścicielki (ale to może zajść z prawdopcxlobieństwem 0,15). Na podstawie minionych doświadczeń pani Edyta wie, że na 90% sąsiadka będzie pamiętać o podlewaniu kwiatów. Po powrocie z ostatniej konferencji pani Edyta znalazła w domu zwiędnięte kwiaty. Jakie jest prawdopodobieństwo, że sąsiadka tym razem zapomniała o ich podlewaniu?

6.    Prawdopodobieństwa tego, że w czasie pracy komputera awaria nastąpi w wyniku uszkodzenia dysku, procesora lub innych elementów mają się do siebie jak 3:2:5. Z kolei prawdopodobieństwo natychmiastowego wykrycia uszkodzenia dysku, procesora i pozostałych elementów są równe, odpowiednio, 0,8; 0,9; 0,9. Znaleźć prawdopodobieństwo natychmiastowego wykrycia przyczyny awarii komputera.

7.    Na stu mężczyzn pięciu nie rozróżnia kolorów, na tysiąc kobiet dwie nie rozróżniają kolorów. Z grupy o jednakowej ilości kobiet i mężczyzn wylosowano daltonistę. Jakie jest prawdopodobieństwo, że to mężczyzna?

8.    Szacuje się, że zaledwie 10% Polaków posiada kartę kredytową. Jakie jest prawdopodobieństwo, że w losowej grupie 8 osób co najmniej jedna będzie miała kartę kredytową?

9.    Liczba e-maili otrzymywanych przez Jasia w ciągu dnia jest zmienną losową o rozkładzie Poissona z wartością oczekiwaną 5. Jakie jest prawdopodobieństwo otrzymania przez Jasia więcej niż dwóch e-maili w ciągu dnia?

10.    Grupę 18 detali podzielono ze względu na wadliwość na 4 podgrupy o licznościach, odpowiednio, 5,7,4,2 dla grupy I,II,III,IV. Wadliwości w kolejnych grupach wynoszą 0.8, 0.6, 0.4, 0.2. Wybrany losowo detal okazał się wadliwy. Niech zmienna losowa X przyjmuje wartości równe numerowi grupy, z której ten detal pochodził. Podać rozkład zmiennej losowej X. Wyznaczyć dystrybuantę, wartość średnią i wariancję X.

1