1

NADZĘDZIE SZTUCZNEJ INTELIGENCJI Lekcja 4: Uczenie sieci neuronowych

CEL: Znaleźć układ wag, aby zminimalizować funkcję błędu

I. Uczenie perceptronu

1. Reguła perceptronowa (dla dyskretnych neuronów)

W_new = W_M+rj(d-y)X

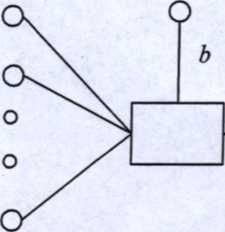
b„ew =b_oUi+ r] (d-y)

gdzie: W_new: nowy wektor wag    x\

W₀id : wektor wag w poprzednim kroku uczenia

bmw : nowa wartość odchylenia    ^Xl

b₀id : wartość odchylenia w poprzednim kroku uczenia

ti    : współczynnik uczenia (wsp. korekcji)

d : żądana odpowiedź

y : otrzymana odpowiedź

X : wektor wejściowy    *n

2.    Reguła DELTA (dla ciągłych neuronów )

W_new = W_oUi+ T] (d-y) f (net)X bnew =b_M+Tj (d-y) f (net)

Pochodne niektórych funkcji aktywacji

a)    Funkcja liniowa J(x) =x —>/’(x) = 1

b)    Funkcja sigmoidalna unipolarna

/w -1—-z# -* m - M-t) [i -x*)i

l + e

c)    Funkcja sigmoidalna bipolarna

/(i) = -^r-i -> XW=|[i-/^!w]

d)    Funkcja tangens hiperboliczny

m=4^ -»• r w -1 - P w

e+e

3.    Algorytm uczenia

Wejście: Ciąg treningowy {(X_h d\), (X₂, d₂),(X_p, d_p)} Wyjście: Wektor wag W, wartość odchylenia b

Krok 1: Wylosuj początkowy wektor wag W i początkowe odchylenie b Krok 2: Dla każdego wektora uczącego X

2.1    Wyznaczy: y=J[WX+ b)

2.2    Uaktualizuj wagi

W_new = W_old +T].(d- y)X    (gdy neuron jest dyskretny)

bneyy =b_oUJ+ TJ (d - y)

W_new = W_M + T].(d - y).f(net) X (gdy neuron jest ciągły) bnew ⁼ b₀id ⁺ tj (d- y).f{net)

Krok 3: Jeśli wagi pozostały bez zmian lub E<E_mm to stop, wpp. powrót do Krok 2