4500

28

Liczby zcspolo_ne

Drugi tydzień • przykłady

27

(cosz)^ł(isin *)^a+ (^ ]|(ćcsz)^ł

(cos t + isin z)* ■

i

cos z)(isin i)¹ + (isin i)⁴

• Przykład 2.7

Konysląjąc ze wzoru dc Moivre a wyrazić:

a)    cos Sr precz funkgę cos z:

b)    mb 6z przez funkcje sin x i coax; c*) ctglr pnea funkcję eig*.

laiwiązank

n) OUksymy wartość wyrażenia (cos r +i sin z) wykorzystując dwa wióry: wzór dr Mo. irtea oui wiór dwumianowy Newtona. Stosując wiór dc Moivrc’» otrzymamy równość

(C04TT i sir. z)³ = co»3r + i*in3z.

2 kolei jr wiotu dwumianowego Newtona wynika równość

(cosiłiwu* = (cosx)* + ^(cosi)^?(i*in x) + ^(cosx)(i^n xf + (isin x)^ł

n cos³r+ Jiajs* xsinx-3cosxsin²x- ssirr x = (co»* x -3rosrsn^: x) + i (3 cos² rsinr - sin³ r) .

Porównując aęfci neaywute prawych stron obu równości otrzymamy

cos3i * «s^,x-3cosrsin^,i eco*r(cos³r -3sin^Jx)

= cosx(cos²x -3+3cos^sx) = COSI (4cos²Z -3) .

b) Obbcijmy warto# wyrażenia (co*x + i»mx)⁶ wykorzystując dwa wióry: wiór de Mwre'a oraz wzór dwumianowy Newtona. Stosując wtór dc Moivro’a otrzymamy róiv-

(cos/ + isin x)° = cos Cr + isin 6r.

Z koki le wzoru dwumianowego Newtona wynika równość

(<os*)‘+ ^(cosr)^ł(i»in *)+ Q X(isin r)^s + Q (cos x)^J(i sin z)⁴

= cos* x + 6icos^s xsin x - 15 cos* sin²z - 20/ cos z sin'¹ z

+15 cos* z sin⁴ z +61 cos z sin¹ x - sin⁴1 a (cos¹1. -15cos⁴ isin² x + 15cos² xsin* x - sin°z)

+i (6 cos* x sin z — 20 cos ’ z sin³ r + 6 cos z sin⁵ x).

Porównując części trojone prawych stron obu równości otrzymamy

sis6x *6cos^łx*in z - 20cos³ z sin³ z + 6cosx$in⁵x.

c*l Podobnie jak poprzednio wyrazimy sin Iz i cos4x prze* sin z i cosx. Ze wzoru dwumianowego Newtona mamy

(coti 4 imu x)^ł » (cos* r - 6cos² x sin² 1 + sin* z) + i (4cos sin z - 4 cos r sin³ x),

Z koki se wzoru de Moivrc’a mamy (cosr + isin i)⁴ a cos4x + isi* <*• Zatem <os4x » eon* * - 6co*² xsin² x+sin* r oraz sin 4/ ® 4cou³ * sin x - 4cosx»in 1. Stąd dla r *£ gdzie i € Z, mamy

cos⁴ x - 6cos² sin²1 + sin* t

et 4* - ^co5'^t’ _ cou⁴x-ócos³wa²z+aiii* z _    siu⁴1

md tr ~ 4cos*sinx-4cosxsin³ x    4co»^łsinz - 4 cos x sin'¹z

577

_m ctg*r-6ctg²x4l 4ctg³x -4ctgx '

• Przykład 2.8

Narysować zbiory liczb zespolonych spełniających podane warunki:

a) Re (*») > 0; b) Im (₂‘) < 0.

Rozwiązanie

W rozwiązaniu wykorzystamy postać trygonometryczną liczby zespolonej oraz wzór de Moivrc*a.

a) Dla z = r (cos _y‘ + isin ?), gdzie r £ 0 oraz 0 { ? < 2r mamy

Re (x^a) > 0 <=> Re {(r (cos p + i sin ^)]²} £ 0 <=> Re jr² (cos2^s + i sin 2p)] > 0 <=> r^łcos2vs % 0 <=+ r = 0 lub r > 0 i cos 2p £ 0 <=* r = 0 lub r>0 i V> € jo, j] U [ U [j,2x) .

Poszukiwany zbiór składa się z dwóch domkniętych obszarów kątowych (zobacz rysunek).

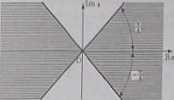
b) Dla » a r (cos p + isin p), gdzie r £ 0 Oraz 0 < y> < 2z, mamy Im I⁶) < 0 <=> Im {(r(cos^ + isin *»)]?] < 0

<=> im (r° (cos 6? + isin 6p)] < 0 <=> r" sin < 0 «=> r >0i sin6p < 0

Bisi