7 1

Piotr Bieranowski - ćwiczenia z WYTRZYMAŁOŚCI MATERIAŁÓW, CZ. VII.

Analiza naprężeń i odkształceń. Hipotezy wytrzymałościowe. Wytrzymałość złożona. ANALIZA NAPRĘŻEŃ I ODKSZTAŁCEŃ SŁOWO WSTĘPNE

W dwukierunkowym (płaskim) stanie naprężenia w dowolnym przekroju określonym kątem a naprężenia normalne i styczne wyznaczmy ze wzorów:

(0

<j_a = (7_{cos² a + c₂sm² a,

(2)

gdzie: cr_{ i a₂ - naprężenia główne, cr_a i x_a - naprężenia normalne i styczne w przekroju a -b, którego normalna tworzy kąt a z kierunkiem naprężeń cr_x (rys. 1).

Aby wyraźniej oznaczyć zwroty (przyjęte za dodatnie) naprężeń <j_a i x_am rys. 1.

Przedstawiono element prostopadłościenny abcd , wyodrębniony (w myśli) z badanego ciała (blachy, powłoki).

Analizę naprężeń wygodniej jest przeprowadzać za pomocą koła Mohra (rys. lc). W przyjętej skali, w układzie współrzędnych er-z, określamy położenie środka Ckoła:

^0C=i(<7₁+<7₂)

i kreślimy okrąg promieniem

CN_l = CN₂

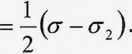
Współrzędne

punktu N, określonego promieniem CN tworzą z osią cr kąt 2a, wyznaczają wartość naprężeń <j_a i z_a zgodnie ze wzorami (l) i (2).

Analizę odkształceń dla trójkierunkowego (przestrzennego) stanu naprężeń przeprowadzamy przy zastosowaniu wzorów, zwanych uogólnionym prawem Hooke'a

A

i r    /    \i

⁼ 4r[^<7i -H

E

<7₂ +<T₃)]

>

(3)

s,=~[o-_}-v(a_t+a₂)]

E

str. 1