CCF20090327000

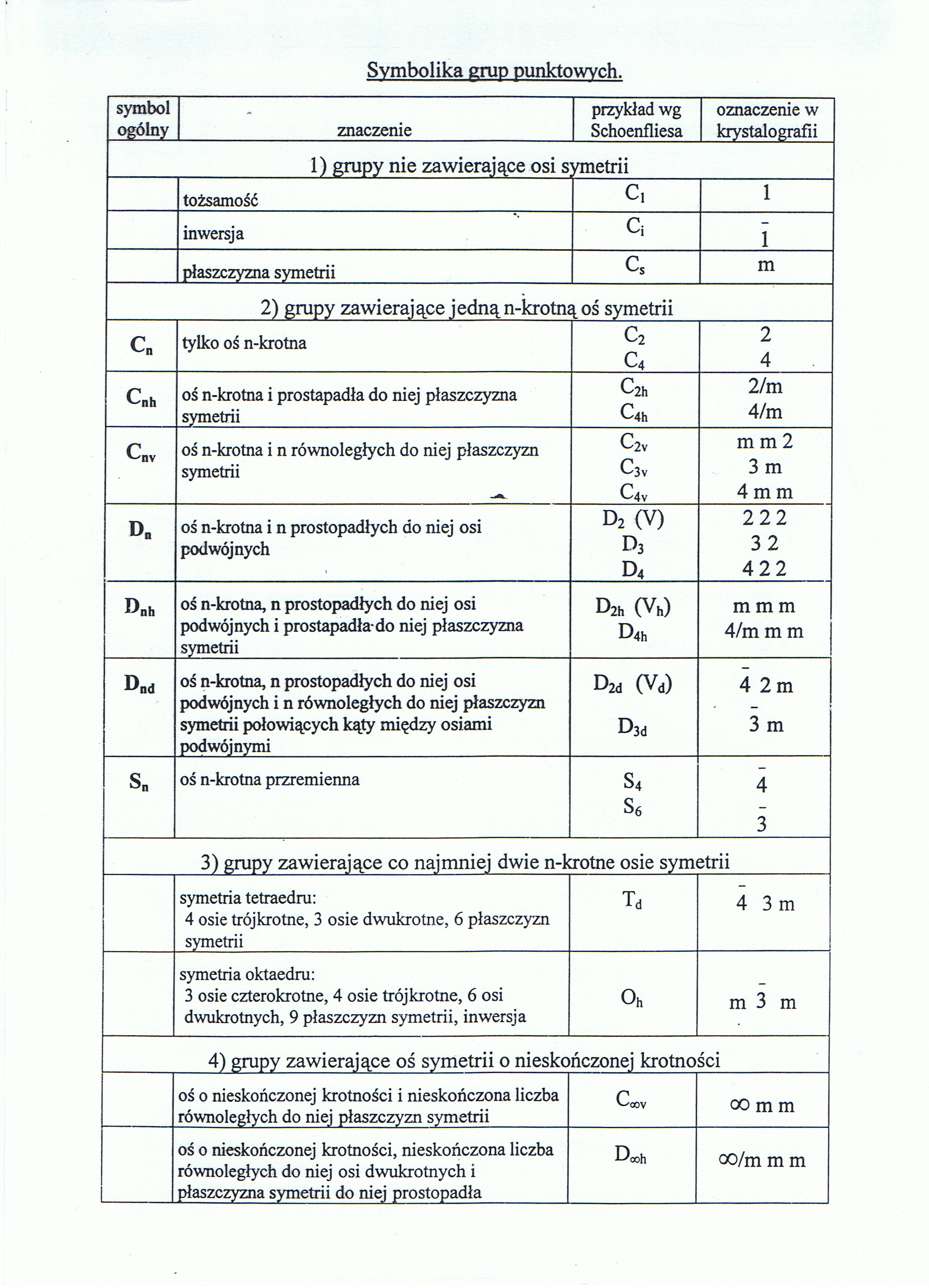
Symbolika grup punktowych.

symbol ogólny	znaczenie	przykład wg Schoenfliesa	oznaczenie w krystalografii
1) grupy nie zawierające osi symetrii
	tożsamość	Ci	1
	inwersja	Ci	I
	płaszczyzna symetrii	Cs	m
2) grupy zawierające jednąn-krotnąoś symetrii
c„	tylko oś n-krotna	C2 c4	2 4
cnh	oś n-krotna i prostapadła do niej płaszczyzna symetrii	C2h C4h	2/m 4/m
Cnv	oś n-krotna i n równoległych do niej płaszczyzn symetrii	c2v C3v c4v	m m 2 3 m 4 m m
Dn	oś n-krotna i n prostopadłych do niej osi podwójnych	d2 (V) d3 d4	222 32 422
D„h	oś n-krotna, n prostopadłych do niej osi podwójnych i prostapadła-do niej płaszczyzna symetrii	D2h (Vh) k>4h	m m m 4/m m m
Dnd	oś n-krotna, n prostopadłych do niej osi podwójnych i n równoległych do niej płaszczyzn symetrii połowiących kąty między osiami podwójnymi	D2d (Vd) D3d	4 2 m 3 m
Sn	oś n-krotna przremienna	s4 S6	4 3
3) grupy zawierające co najmniej dwie n-krotne osie symetrii
	symetria tetraedru: 4 osie trójkrotne, 3 osie dwukrotne, 6 płaszczyzn symetrii	Td	4 3 m
	symetria oktaedru: 3 osie czterokrotne, 4 osie trójkrotne, 6 osi dwukrotnych, 9 płaszczyzn symetrii, inwersja	oh	m 3 m
4) grupy zawierające oś symetrii o nieskończonej krotności
	oś o nieskończonej krotności i nieskończona liczba równoległych do niej płaszczyzn symetrii	c Vxoov	oo m m
	oś o nieskończonej krotności, nieskończona liczba równoległych do niej osi dwukrotnych i płaszczyzna symetrii do niej prostopadła	Dooh	oo/m m m