DEgz1 2009 odp

Egzamin z matematyki dyskretnej 19 czerwca 2009

Imię:

k

0

J

79

~D~

Nazwisko:

P

1

0

|Q

0

c;

5

JA

l

Grupa: i

‘Numer Indeksu: j

1.    Czas rozwiązywania 120 minut.

2.    Ewentualne wątpliwości związane z niejednoznacznością sformułowań w zadaniach należy umieścić obok udzielonych odpowiedzi.

3.    Dozwolone jest korzystanie z pomocy w formie własnoręcznych notatek i wydruków slajdów z wykładu. Nie wolno korzystać z książek i urządzeń elektronicznych.

4.    Zbiór liczb naturalnych nie zawiera zera: Os A/.

5.    C„oznacza cykl o n wierzchołkach, P„ oznacza ścieżkę o n wierzchołkach

6.    W trakcie egzaminu nie wolno opuszczać sali przed oddaniem pracy.

Uwagi:

Zad. 1. (9 pkt.) Czy następująca funkcja zdaniowa:

[A\B = C\B a B\A= B\C] => [Au C c B v A u B q C v A n B n C = 0]

jest prawdziwa dla każdych trzech podzbiorów zbioru {1,2,3}? (Tak/Nie)?

Jeśli odpowiedziałeś "Nie", przedstaw kontrprzykład przez wskazanie trzech (niekoniecznie różnych) zbiorów A, 5,Cę {1,2,3}, dla których ta funkcja staje się zdaniem fałszywym.

Kontrprzykład (opcjonalnie): A

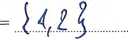
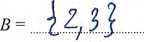
Zad. 2. (9 pkt.) Uzupełnij poniższe formuły symbolami zmiennych zdaniowych tak, aby powstałe schematy logiczne były logicznie równoważne schematowi (p a r) -» (q -> r). Możesz używać wyłącznie symboli zmiennych zdaniowych (np. p, q, r, s). Dopisywanie spójników logicznych jest niedozwolone. Jeżeli uważasz, że w którymś przypadku takie uzupełnienie nie jest możliwe, wpisz obok formuły sfonnułowanie "brak rozwiązania".

(a) (pv~j?.)vj    [f C, - Jo co o Cs

(b) r->(£.->n    / r -> C    Uy}-^'

(c) (<?^j    p) ^ Cp

Zad. 3. (9 pkt.) Definiujemy następujące predykaty: P(x) - x jest psem, C(x) - x jest człowiekiem oraz fV(x, y) - x jest właścicielem y. Wyraź w języku rachunku predykatów pierwszego rzędu następujące zdania: (a) Żaden pies nie jest człowiekiem, (b) Każdy pies posiada właściciela, który jest człowiekiem, (c) Żaden pies nie jest właścicielem żadnego człowieka. Nie wolno używać żadnych innych symboli niż nawiasy, wymienione powyżej predykaty, zmienne, kwantyfikatory oraz spójniki logiczne.

(c).

Zad. 4. (9 pkt.) Udowodnij, że dla dowolnej liczby naturalnej n, n prostych rozcina płaszczyznę na nie więcej niż (n² + n + 2) / 2 spójnych obszarów. Dowód przedstaw na odwrocie strony. £ ₀y _D f,j    >tX (t)

Zad. 5. (9 pkt.). W zbiorze A = {1, 2,..., 10} zdefiniowano relację binarną £:

o (x < y a x mod 2=y mod 3).

Niech R =p(z(S)). Dla zbioru częściowo uporządkowanego (A, R) Wyznacz:

(a)    Wszystkie elementy minimalne:    .....................................................

(b)    Wszystkie elementy maksymalne:. O..................................

(c) Najdłuższy łańcuch: .2.^ IQ..f 3..f. d..Q.

Na odwrocie przedstaw diagram Hassego tego porządku.

4

⁵ «

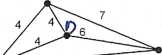
Zad. 6. (9 pkt.) Dla grafu przestawionego powyżej wyznacz:

(a)    Wagę minimalnego drzewa spinającego:........................ CO, cB)

(b)    Długość optymalnej trasy chińskiego listonosza:......3 ^.......)

(c) Długość optymalnej trasy komiwojażera:.. a3    l $o-><?-) c.)

Zad. 7. (10 pkt.) Wyznacz liczbę podgrafów pełnego dwudzielnego grafu K₃ 5, które są:

(a) Izomorficzne z grafem K_iy

(b) Izomorficzne z grafem K₂?_\ .£$){ Sj ^ £)

V! isj v_

(c)    Izomorficzne z grafem C₄:.....[ %

(d)    Izomorficzne z grafem P₃..