IM8

Tw sinusówu

sina. sinp. siny

Tw cosinusów (Carnota)

a²=b²+c²-2bc cosa b²=a²+c²-2ac cosb c²=a²+b²-2ab cosy

Odległość dwóch punktów na płaszczyźnie

IAB | = V(Xb - Xa)² + (Yb ■ YaJ² Środek odcinka AB ma współrzędne:

_{ Xą+Xb Ya+Yb ■.

I 2    ' 2 ^}

Odleg. punktu P(xp,yp) od prostej "L" na płaszczyźnie:

L : Ax + By + C =0    A² + B² > 0

_ / Axp + Byp + C /

-Ja? + b²

Współrzędne wektora na płaszczyźnie:

AB = [x_B - x_Al y_B - Ya]

Długość wektora na płaszczyźnie :

AB = V(x_B - x_A)² + (y_B - Ya)²

Okrąg:

Okręgiem o środku O i promieniu r (r > 0 ) nazywamy zbiór punktów płaszczyzny, których odległości od środka O wynoszą r.

x²+y²=r

Równanie okręgu:

(x - a)² + (y - b)² = r²

x² + y² - 2ax - 2by + c = 0    S=(a_tb)

c = a² + b² -r² a² + b² -c > 0

Równanie ogólne prostej

Ax + By + C = 0

Równanie kier prostej

y = ax + b

Proste y = a-|X + bi i y = a₂x + b₂ są:

-    równoległe O a-i = a₂

-    prostopadłe O a^ = -1

Równoległość prostych na płaszczyźnie:

Dwie proste są równoległe jeśli leżą na jednej płaszczyźnie i nie mają żadnego punktu wspólnego lub się pokrywają.

Wielokąty:

Wzór na sumę kątów wewnętrznych dowolnego wielokąta:

(n-2)*180° n-liczba boków

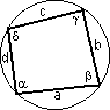
Kąty na czworokącie

a+c = b+d a+y = |3+5

Przystawanie trójkątów:

1.    cecha przystawania A-ów Dwa trójkąty są przystające jeśli boki jednego trójkąta są odpowiednio równe bokom drugiego trójkąta.

|AB|=|A'Bj i |BC|=|B'Cj i |AC|=|A'C'| {BBB}

2.    cecha przystawania A-ów

Jeżeli dwa boki i leżący między nimi kąt jednego A-a są równe odpowiednio dwóm bokom i leżącemu między nimi kątowi drugiego A-a, to te dwa A-y są przystające.

|AC|=|A'C'| i |BC|=|B'C'| i Z ACB=Z AB'C' {BKB}

3.    cecha przystawania A-ów

Jeżeli bok i dwa kąty do niego przylegające jednego A -a są odpowiednio równe bokowi i dwóm kątom do niego przylegającym drugiego A-a to trójkąty te są przystające.

Z BAC = Z BA'C' i ZABC = ZA'B'C' i |AB|=|A'B'| {KBK}