IMAG0094

4. Operatory różniczkowe: gradient, dywergencja, rotacja

Gradient

V,h0..y*-» 2 e- ^x-(x² + 2*y³) + e²'^x-(₂.y³ _{+ 2}._x) 2 2-a

v\ b(a.y) —> 6-x-y -e

Vj.bti.yl

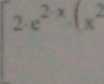
2 x-y³) + e²'* (2-y³ 6-x-y²e²*

cośOi *in(x)

V, fu» -----—

%

^Zei>y uzy*kać wynik nu-./.ego działania wybieram. ,

»-valuatiunpr/ycfak I taluafrKymbollrelly lubCirlf

fW

(«o) *1 (*2)

Uwaga Ainkcja p(a) jeat w tym przypadku fUnkcję iknfamJ od if/rcb Imiennych, a więc akładowycli wektora, ala ouczonego tylko pnjedyhczfl llięm *•_____1

V,pt«)

I

V_vp(\)

•' mi ^r(

(*o)²'(*2)⁵ j(*o)² *1 (*a)²

♦ I l9J

Nalary zwrócić uwagę. U a Jeat wektorem o aklądowych] |*ii.    ►-W programie Mallicad domyślnie plenmyml

wak a/niklem jeat zero

1'rrypmunlritlr do deklamcjl lUnkoJI ubywamy akrolu Dlilft 1

Deklaracja » Jaku wek lont o alalych wartościach.

W tym celu / palety Matrli rnotenty wybrać przycisk Mairli nr Vucior lub nn kliiwiniiir/c ( tr i M

(kadicnt Hinkcji akalamej p (•rektor)

hn<Mtcut) pcflwtM nwme Utedu \ tako muenacj (będzie to potn jpnlaa* wtaiokon\«k

:ebnc do

/jjefinio^onia p

\ \

Dywergencja

Definiujemy operator dywergencji w układzie konezjańikim

div(B,x,y,z)

— B(x,y,z)o + —B(x,y,z)| +—B(x,y,z)₂ dx    dy    dz

Uwaga: B jest wektorem o składowych B„. B,. B₂

B(x,y,z)

x-z '

2

-y

, 2

\2 x y)

Dcfinujeray konkretny wektor opisujący pole wpizestrzcni kanezj sit sklej

Obliczeni* symboliczne

div(B,x,y,z)z - 2-y

Obliczenia numeryczne

dlv(B, 1,1,1) =» I dlv(B,2,3,3) ■ -3

Wynikłam dy wsrgsncjl jest wartołć liczbowi (dywergencja jest tkalaram).

Rotacja

curl(H,x,y.z):

Definiujemy upenitor rotacji w ukliulzle katttijafisklm

—    H(x.y./)2

dy

—B(\.y.z)o dz

—    Il(x,y.z)| V.dx

—    H(x.y./)|

dz

—    B(x,y,z)2

dx

—    B(x.y.z)o

dy    ,

■t

Obliczenia synthoUczne

curUU,x,y,z)_x _ 4._Vy

0

Obliczenia numery czne

	2 ^		8 "
curl(B. 1,1,1) =	-3	curMB.2.3.3) =	-22
	,0 >		k ^0 z

5