scan 4 (5)

5. MAGNETOSTATYKA

wektorowego automatycznie gwarantuje, że V • B = 0 (ponieważ dywergencja rotacji zawsze znika); prawo Ampere’a przybiera postać

(5.60)

VxB=Vx(VxA) = V(V • A) - AA = J.

Potencjał elektrostatyczny nie był wielkością wyznaczoną jednoznacznie, do V można bez zmiany natężenia pola elektrycznego E dodać jakąkolwiek funkcję, której gradient znika (czyli stałą). Podobnie, do potencjału magnetycznego można dodać dowolną funkcję, której rotacja znika (czyli taką. która jest gradientem skalara). i nie zmieni to indukcji pola magnetycznego B. Wykorzystamy tę swobodę do wyeliminowania dywergencji A:

V ■ A = 0.

(5.61)

By wykazać, że zawsze jest to możliwe, załóżmy, że dywergencja naszego pierwotnego potencjału A₍₎ nie znika. Jeśli dodamy do niego gradient X (A = A₀+VA), to dywergencja nowego potencjału jest równa:

V • A = V ■ Aq + AX.

Równanie (5.61) jest spełnione, jeśli istnieje funkcja X będąca rozwiązaniem równania

Aż. = —V • A₀.

Jest to jednak matematycznie tożsame z równaniem Poissona (2.24),

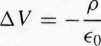
z V ■ Ao zamiast p/eo w roli „źródła”. Równanie Poissona umiemy rozwiązać —jest w nim zawarta cała treść elektrostatyki (znaleźć potencjał dla zadanego rozkładu ładunku). W szczególności, jeśli p znika w nieskończoności, rozwiązanie dane jest równaniem (2.29):

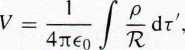
tak więc przez analogię, jeśli V • Aq dąży do zera w nieskończoności, to

Jeśli V • Ao nie dąży do zera w nieskończoności, to musimy posłużyć się inną metodą znalezienia właściwej funkcji X, tak jak innym sposobem znajdujemy potencjał elektrostatyczny w przypadku, gdy ładunki są zlokalizowane w nieskończonym obszarze. Jednak podstawowy wniosek pozostaje ten sam: Zawsze można wybrać potencjał wektorowy w taki sposób, by był bezźródłowy. Można to wyrazić inaczej: definicja B = V x A określa rotację A, natomiast nic nie mówi o jego dywergencji — możemy wybrać ją dowolnie, a zero jest zwykle najprostszym wyborem.