Image2892
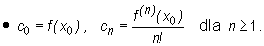
• Co = f(xo) > C
ni
dla n > 1.
Wyszukiwarka
Podobne podstrony:
Image2546 y(x) = 0(x) + Co = <2>(x) + y„ - ®(xo) = y„ +
Image2010 co + = [ 0 + co +] r 1 Uf- »4r-U Uf «,4r-U co + =^— + Zuz+ zu UUII =-—- UJ II
Image2013 = — co lim bn = - co => lim an
Image2019 + co + co
Image2134 CO ĄZ^sin- n=1 n
Image2175 V1 _ 2"ł1 . ni b„ (n + 1)! 2" 2 n + 1 lim - 1 + 1
Image233 Jeżeli funkcje przełączające dla wejść J i K zostaną przekształcone w następujący sposób: j
Image2440 I I co fc?
Image2443 I co ć-ł X T- I COI X XCsJ I co OJ XI IX£l
Image2466 co i UJ X_ęę ■o co I OJ + x ii
Image2468 co-8 x i CO
Image2524 Ponieważ fl(x) = ^rr dla x*0 orazpochodnata nigdzie się n ie zeruje.to
Image2890 f( X) = Xcn( x~xu)n dla wszystkich xe(a,b), to n=0
Image2891 • f (X) Ą ^ncn(x-xQ)n~ dla wszystkich xe(a,b), r>=o
Image2893 Wiemy, że(*) 7-]-=h-vnxn, l + x n=0 dla xe(-1 V, zatem funkcja f(x)= -— ma szeregMacLaurin
Image2911 CO j xn. Ponadtodla (n + 1)-szej reszty we wzorze Ma cLa u ri nad la e n=on- x mamy oszac
więcej podobnych podstron