image2
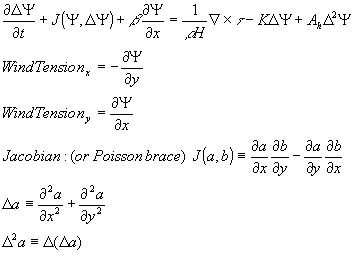
r-KA^Y
^M'ł'.A'ł')+^--Lv
dt dx ,di
WindTensionv = --
* ty d^¥
WindTension„ =-
v dx
Jacobian : (pr Poissonbrace) J{a,b)
da db dx dy
da db dy dx
Wyszukiwarka
Podobne podstrony:
img067 (18) dr dt dx dy dz , di -1 + —1 + — k +x -+ dt dt dt dt , d j , y—— +
Image22 3DIALOGVS LV S CI ANI NVPER G GRECO IN LA* TIN VM VERSVSn 1NTBR# LOÓWTOUES PO& TA BT AST
Image22 3DIALOGVS LV S CI ANI NVPER G GRECO IN LA* TIN VM VERSVSn 1NTBR# LOÓWTOUES PO& TA BT AST
Image22 3DIALOGVS LV S CI ANI NVPER G GRECO IN LA* TIN VM VERSVSn 1NTBR# LOÓWTOUES PO& TA BT AST
Image22 3DIALOGVS LV S CI ANI NVPER G GRECO IN LA* TIN VM VERSVSn 1NTBR# LOÓWTOUES PO& TA BT AST
Image243 Ar ŁV ~~~¥
Image251 ^ = k-u lub T— = u dt dt
image3 dAV dt ~dx maxąl? ,diB: •Vx — AT + /B/g3
Scan10032 o ex ex +1 W W2(x) = Wi(x) = 0 ex I ex + l -1 Ąg* ex + !==€ dx = di ex =/-li 1
065 2 128 Dla 1=0,25 mamy d2y _i
OLOGIA [ADAŃ WRAZ Z ODPOWIEDZIAMI Dt» kanćitiatfrM na Urvwm>t«y Mfóyanc i k*runJu
więcej podobnych podstron