Image3029
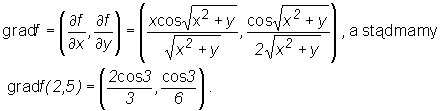
gratf =
grad 1(2,5)
xcos-yx2+y cosJx2 + y
9
xć +y
‘ 2-jx2 +y
, a stąd ma my
(2cos3 cos^l
J
Wyszukiwarka
Podobne podstrony:
419 § 3. Niektóre zastosowania teorii funkcji uwikłanych Rugując dt z równości df=dx+dy+dz+dt=0
Image3092 3F 3F du dv = df df dx1 dy dx dx du dv dy dy du dv 2e2xcosyJ-e2xsiny 2 u -
Image3117 ĆF df dx df dy x x3 ? - =--+--?-=QX+QX -3x dx dx dx dy dx
Image3451 badźgradF = df dx. ■ grad* .
Image3092 3F 3F du dv = df df dx1 dy dx dx du dv dy dy du dv 2e2xcosyJ-e2xsiny 2 u -
Image3199 df, , — (x0Jo) dy ljm f(xo,yo + tł)-f(x0ly0) h-»0
S(x) = dY = df{x) dX dx(2) Dla przetworników liniowych czułość przetwornika jest stała co do wartośc
dF dF dF dv dx, dy dx,4 f dy de dF I dv _d__dF_ dx2 f dy l ĆtCi - 77(^1»x2 )dxldx2 =0 Njowolna
więcej podobnych podstron