img083

83

j *2    Sau^t. Sygnał wejściowy *_s(t) filtru jest dany zależnością

(1.3.1), sygnał wyjściowy jest zateai równy

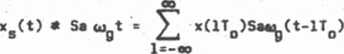
Na wocy twierdzenia o próbkowaniu sygnał wyjściowy filtru jest nie znie-kształconyai sygnałem oryginalny* x(t). Otrzymujemy wobec tego poszukiwany związek

x(t) «

(1.3.4a)

wyrażający sygnał ciągły przez jego próbki. Szereg (1.3.4a) jest nazywany w literaturze szeregiem Kotielniko.ia - Shannona, a funkcja Sa<*i t funkcją próbkującą. Z (1.3.4a) wynika, że wartość sygnału w dowolnej ustalonej cbwili czasu t i kT_Q wyraża si . liniową koaibinacją jego próbek x(lT₀),

1«0,—1,—2,...; współczynniki tej koaibinacji są równe Saa)^(t - 1T₀). Ponieważ Saa>_Q(kT₀-lT₀) = 0 dla k i 1, to wartość szeregu Kot*.elri..owa -- Shannona dla t * kT₀ wynosi dokładnie x(kT₀>. Z tego powot * "ów i się, że próbki sygnału pobierane z częstotliwością Nyquista są od siebie niezależne.

M przypadku co_Q > 2*u₀ sytuacja nieco się komplikuje, gdyż filtr odtwarzający (o impulsowej funkcji przejścia h(t)) wcale nie musi być idealny (prostokątny). Zależność (1.3.4a) Kodyfikuje się wtedy do postaci

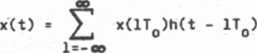
(1.3.4b)

Impulsowa funkcja p'zejścia h(t) zazwyczaj nie'spełnia już teraz warunku h(nT_Q) * 0,n = — 1,—2,... Oznacza to, że próbki sygnału pobierane z częstotliwością większą od częs*ct iwości Nyquista nie są już niez; lsżie, gdyż

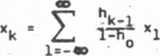
1/k

(1.3.4c)

“o ¹ X<"V* ^hn * ^h(nTo>