img126

126

współrzędnych możer^- obliczać albo za pomocą maszyny do liczenia i tablic funkcji trygonometrycznych, albo na maszynach elektronicznych z gotowymi programami.

Obliczone i skontrolowane przyrosty Ax i Ay samu jeny i kontrolujemy zgodność lcb sum z warunkami osiowymi rzutów w ii^śl równań

X* s x + [l . oosa] ♦ [dx]

(75)

7_k « 7_p + C¹ . sina] + [dy]

gclzlei y^ ozcoczeją wartości współrzędnych punktu końcowego,

Xp, 7p oznaczają wartości współrzędnych punktu początkowego,

C<Łz], Cdy] oznaczają sumy poprawek do tych przyrostów.

W poligonie zamkniętym    oraz y_p = y^, wobec czego

[1 cos a] + Cda] * O

(76/

[l sina] * [dy] = O

Zgodnie z definicją odchyłek, sumy [dr] oraz [dy] wyrażone jako odchyłki

(77)

f_x - [ds] = Cl cos ot] fy = r<S7]« Cl sina]

stanowią o wartości liniowego nia zamknięcia poligonu w myśl wzoru

-L

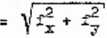
(78)

Jest to odległość liniowa punktu wyjściowego w ciąga zamkniętym od położenia tego samego punktu -wyznaczonego na podstawie sucy obliczorych przy-rostów'współrzędnych. Odchyłka liniowa nie może przekraczać dopuszczalnej odchyłki według Instrukcji dla odpowiedniej klasy poligonu

(79)

■P

^ZL ^XI dop.

Jeżeli przekroczenie tej odchyłki nie wynika z błędów rsohuakowych, a powstało w wyniku pomiarów, należy wówczas powtórzyć pomiar boków poligc-

Sczdzielenie odchyłek sum. przyrostów dokonuje się proporcjonalnie do długości poszczególnych boków poligonowych, choć w pewnych przypadkach dopuszcza się też inąy ich rodział. Wartości te dodajemy (za znakiem przeciwnym) do poszczególnych przyrostów współrzęiuych, kontrolując, czy tak poprawione przyrosty współrzędnych spełniają wartości założone geometrią figury. Czynność tę nazyr/acęr wyrównaniem. Po wyrównaniu przyrostów .współrzędnych przystępujemy do obliczenia wartości współrzędnych poszczególnych punktó-j.- poligonu. Przebieg obliczenia poligonu w formularzu przedstawiono ns przykładzie poligonu dwustronnie dowiązanego*