img212

(124)

212

^& s E ^Ii^ri+1 ^{słn (0,}±*1 " ^oci⁾ 1

§uma różnic

= o

<“2 - «S> ^{+ (}“3 - ^a2^{) + (}“l - “3> * t. ^(orl+1 - “l¹

zatem dla wicloboku o n Wierzchołka oh kontrola obliczenia różnic (ot_i+/j - Of^) stanowi równanie

£

(«_i+1 - «i) = o

(125)

5. Obliczenie powierzchni na pedsta7/ie współrzędny oh prostokątnych: anjąc współrzędne prostokątne x, y wierzchołków wleloboktt w układzie,

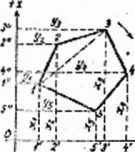
Kys. 227

Jak na rysunku 227, ponumerowanych 2£odnie z ruchem wskazówki zegara, możemy obliczyć jege powierzchnię za pomocą + zW. wzorów Gaussa-l^Huillie-ra-„ 7/asadę tych wzór w można wyjaśnić na rysunku 227 dodając i.odejr^jąo powierzchnię trapezów o bokach wartości r ędnych i odciętych;

Dla wielobofcu o n wierzchołkach 'wzory są na-*~*^s stępujące:

2P

.+1 " ^yi-1)

(126)

^yi <*i+i " *i-n>

Zv wzorów tych otrzymujemy dwa wyniki na P, które muszą być identyczne (kontrola obliczenia ?)♦

kontrolę obliczenia różnic współrzędnych doją równania:

U

Z! *^yi+1 “ ^yi-1* ^{= 0} 1

(127)

n

^^xi+1 *■ *1-1) ^{= 0}

j/zery Gausaa-1'Huilliera można stosować również do obliczenia powiorz-ch;i pc3;ierzonaJ w sposób podany na rysunku 228, zakładając, że poozątek