MAT12

2)

12

f —di— = 4 f-dli-₌ Jl f

^J Ja^W ‘ ^J Ja²-a²u² Ml ^j

—dl!— = _Sgn/1 • arcsinw = sgn^arcsin-y-

^A

(podstawienie: t = Au => dt = Adu).

f ■ ■■ dl = f    ~^u—u +A.₍i_u _ f djj_ _ |_n|_M|₌ |_n / + Jt² + A

^J 7/² +/ł ^J    2ir    J

Podstawienie: V/² + A = u - t => I² + A = u² - 2tu + t^z => t = ¹¹ . ^A => dt = ^u„\^A du; Jt² + A =

2 u    2 u²

Przykłady

1.

■Y- l

= arcsin

.r-1 -/

f dx ₌ r dx ^J 73 + 2.v - .y^{2 J} ^4 - (a- - l )²

Postać kanoniczna: a/² + Ar + c = r/^r +

2.

f * -1	f * - 1	[
^J v/4a-^2 + 4.y - 3 ^J	M*+*y-^Ą	y

dx

f ^dt In	/ + Jt^2 - 4	= 2 ln	2.y + 1 + 7 4.y^2 + 4.y - 3
^J 7/^2-4

Zadania

Obliczyć następujące całki

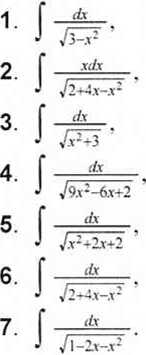
5.2.2. f ^U['^M dx

']ax²+bx+c

Tw.

W_H{X)

Jax² + bx + c

■ dx = W„-\(x) Jax² + bx + c + /ć|

dx

yjax² + bx + c

Przykłady

1.

*³-x+J_d_x = (_Ax2 ₊ Bx + C) y.Y² + 2.Y + 2 + K [ ^J-^Y y.Y² + 2x + 2    ^J y.Y² + 2.v + 2

Ostatnią równość różniczkujemy obustronnie i otrzymujemy

^A'³ ~^A'⁺ 1    = (2/l.r + B) y.v² + 2.v + 2 + (//.Y² + &y + C) , ^Zv + ²-+ ^K |. 7a² + 2.y + 2

y.Y² + 1y + 2    2/y² + 1y + 2 y.Y² + 2y + 2

Opracował: Marian Malec